© 2021 Ольшевский Андрей Георгиевич репетитор по математике, физике, информатике, программированию по Скайп

Сайт супер код ру super-code.ru наполняется ценными темами, которые можно скачать бесплатно

Векторы на плоскости и в пространстве, способы решения задач, примеры, формулы (окончание)

Векторы на плоскости и в пространстве веб-страницы: 1 2 3

41 Решение задачи № 14 ЕГЭ Демо 2021 проф с помощью векторов

41.1 Задача № 14 (1) ЕГЭ Демо 2021

Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 6. Точки M и N— середины рёбер AA₁ и A₁C₁ соответственно.

а) Докажите, что прямые BM и MN перпендикулярны.

б) Найдите угол между плоскостями BMN и ABB₁.

Решение

У правильной призмы в основании лежит правильный многоугольник и боковое ребро перпендикулярно основанию. У правильной треугольной призмы в основании равносторонний треугольник. Изобразим на рисунке правильную треугольную призму со всеми ребрами a равными 6. Выберем систему координат так, чтобы начало координат лежало в плоскостях BMN и ABB₁. Точка B принадлежит этим плоскостям, поэтому точку B принимаем за начало координат как показано на рисунке

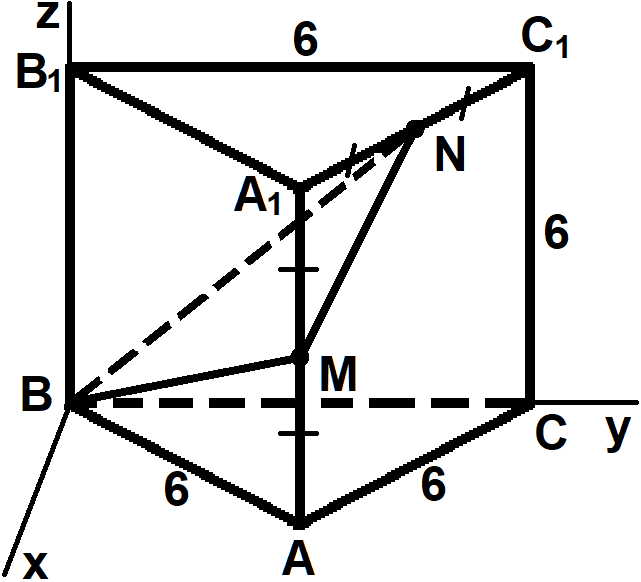
а) Докажем, что прямые BM и MN перпендикулярны. Рассмотрим снизу основание ABC

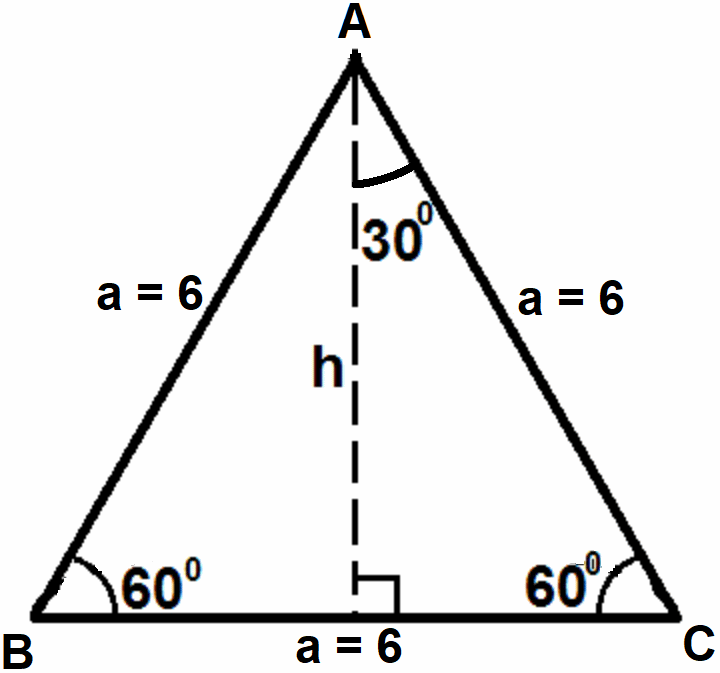
Высота основания, являющегося равносторонним треугольником

h = a sin60⁰;

Координаты точек в выбранной системе координат

B(0; 0; 0);

Определим координаты направляющих векторов прямых BM и MN. Вектор проведен из начала координат, поэтому координаты конца вектора (точки M) являются координатами вектора

Координаты вектора равны разности координат конца вектора и начала

Скалярное произведение векторов в координатах

Скалярное произведение направляющих векторов равно 0, следовательно, прямые BM и MN перпендикулярны.

б) Найдем угол между плоскостями BMN и ABB₁. Для этого сначала определим нормальные векторы и уравнения этих плоскостей.

Определим нормальный вектор и уравнение плоскости ABB₁. Для этого сначала определим координаты 2-х точек, задающих прямую A₁B₁, не проходящую через начало координат и лежащую в плоскости ABB₁. Координаты этих точек, лежащих в плоскости ABB₁

B₁(0; 0; 6).

Общее уравнение плоскости ABB₁

ax + by + cz + d = 0.

Плоскость ABB₁ проходит через начало координат, подставим нулевые координаты x, y, z в общее уравнение плоскости и получим d = 0. Тогда общее уравнение плоскости ABB₁ принимает вид

ax + by + cz = 0.

Неизвестно 3 коэффициента a, b, c. Подстановка координат двух точек A₁ и B₁ в общее уравнение плоскости дает систему 2-х уравнений. Если принять какой-то коэффициент в общем уравнении плоскости равным единице, тогда система 2-х уравнений позволит определить 2 оставшихся неизвестными коэффициента.

Если одна из координат точки нулевая, то за единицу принимается коэффициент, соответствующий этой координате. Если у какой-то точки две координаты нулевые, то за единицу принимается коэффициент, соответствующий одной из этих нулевых координат.

У точки B₁(0; 0; 6) координата x нулевая, поэтому принимаем a = 1, тогда система 2-х уравнений позволит определить 2 оставшихся неизвестными коэффициента b и c:

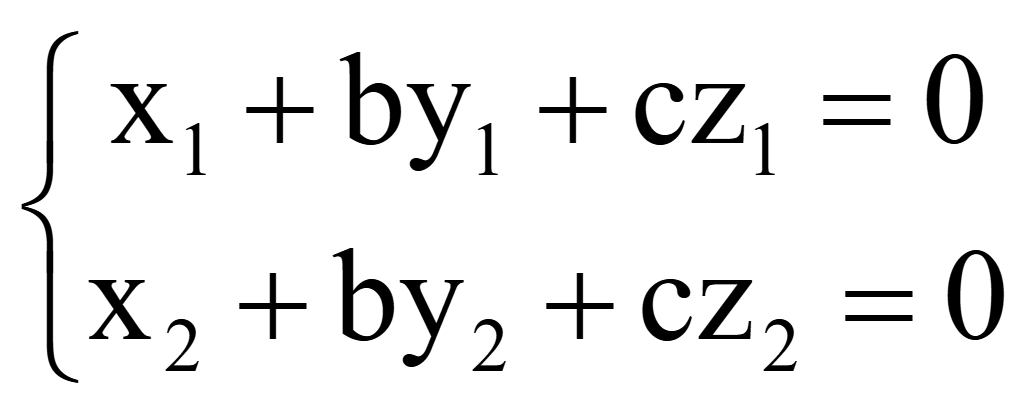
Подставим координаты точек A₁ и B₁

B₁(0; 0; 6):

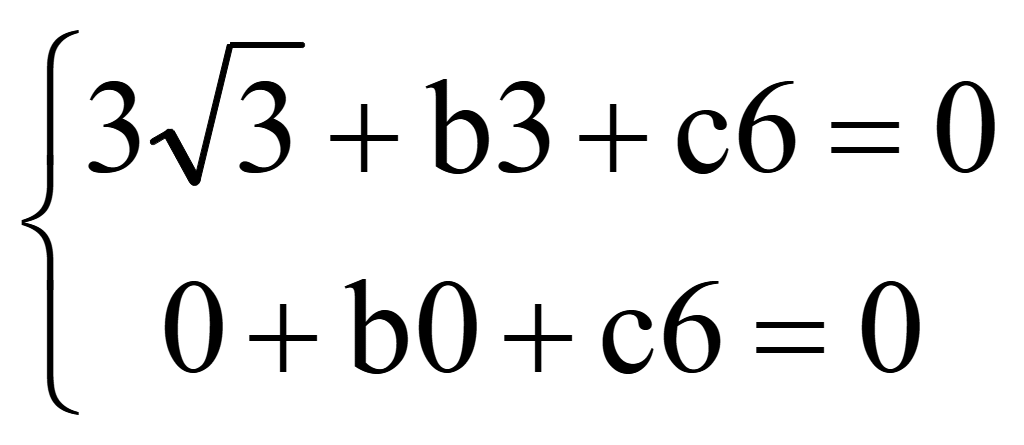
Из 2-го уравнения нашли c и подставили в 1-е уравнение

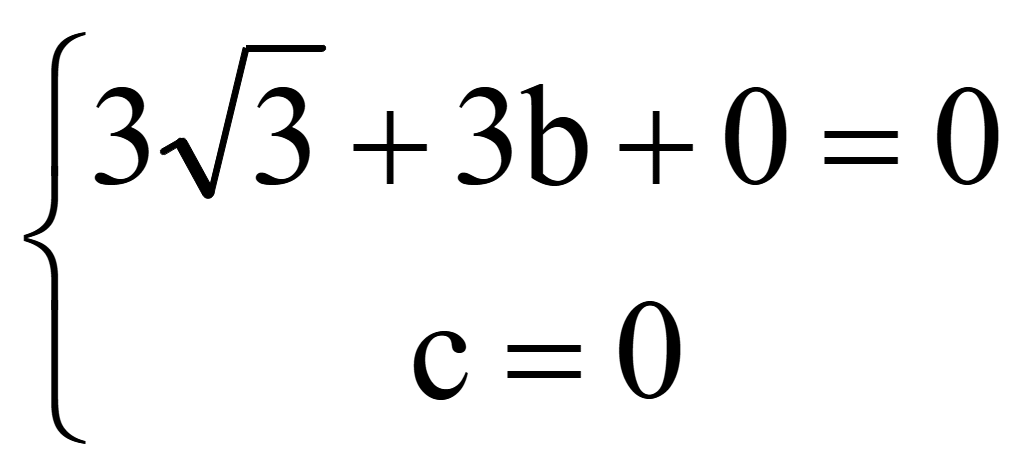
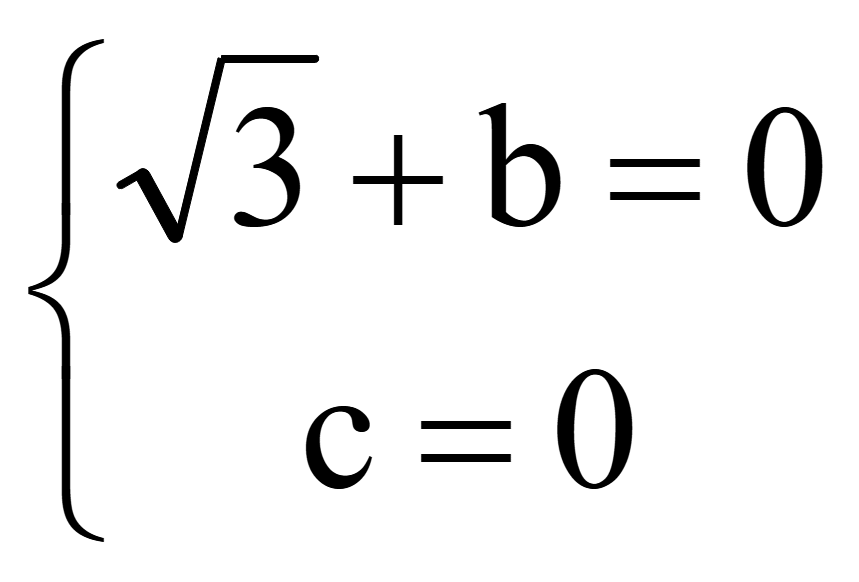
Из 1-го уравнения нашли b

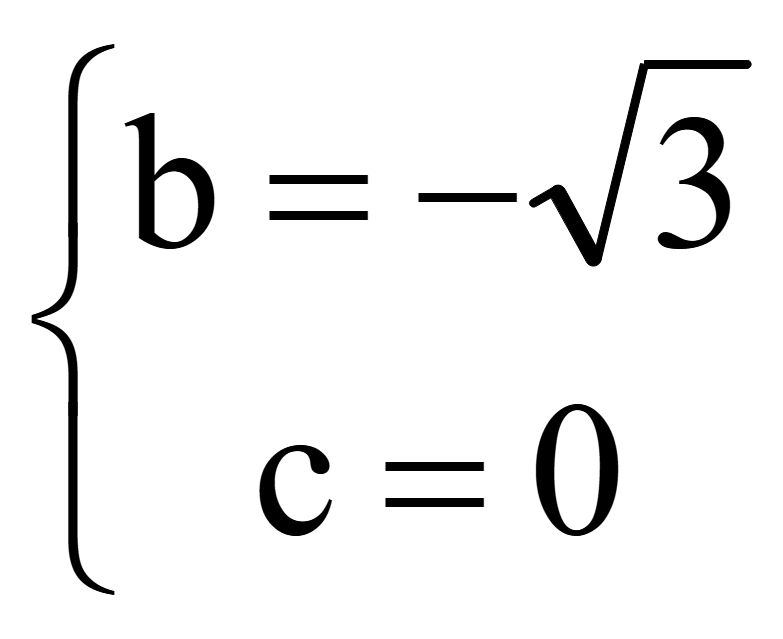
Нормальный вектор плоскости ABB₁

Уравнение плоскости ABB₁

Определим нормальный вектор и уравнение плоскости BMN. Координаты точек M и N, лежащих в плоскости BMN и не проходящих через начало координат известны:

Нулевых координат нет, поэтому произвольно принимаем a = 1, тогда система 2-х уравнений позволит определить 2 неизвестных коэффициента b и c:

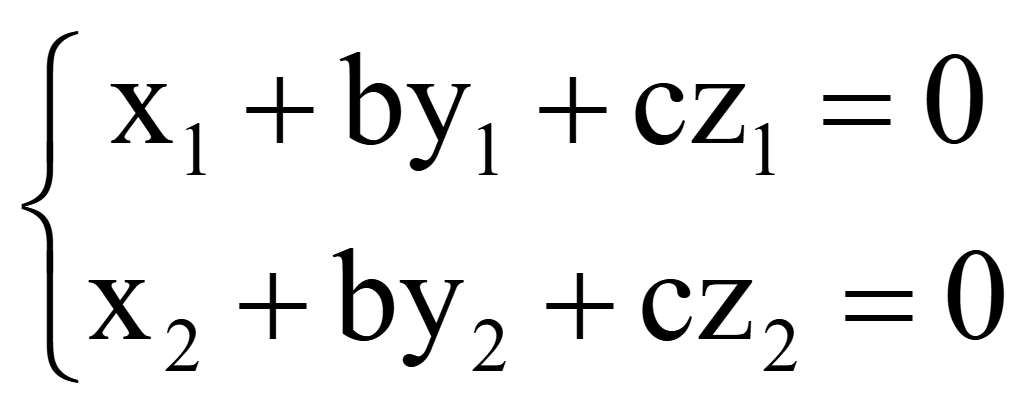
Подставим координаты точек M и N

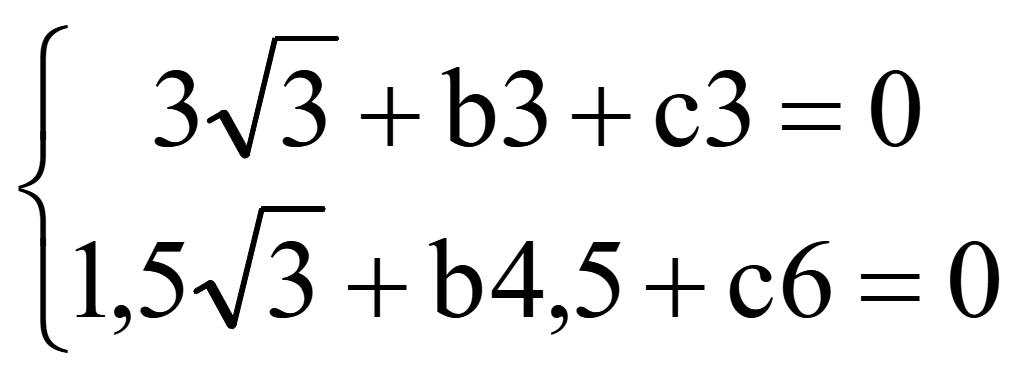
Сократим первое уравнение на 3 и второе на 1,5

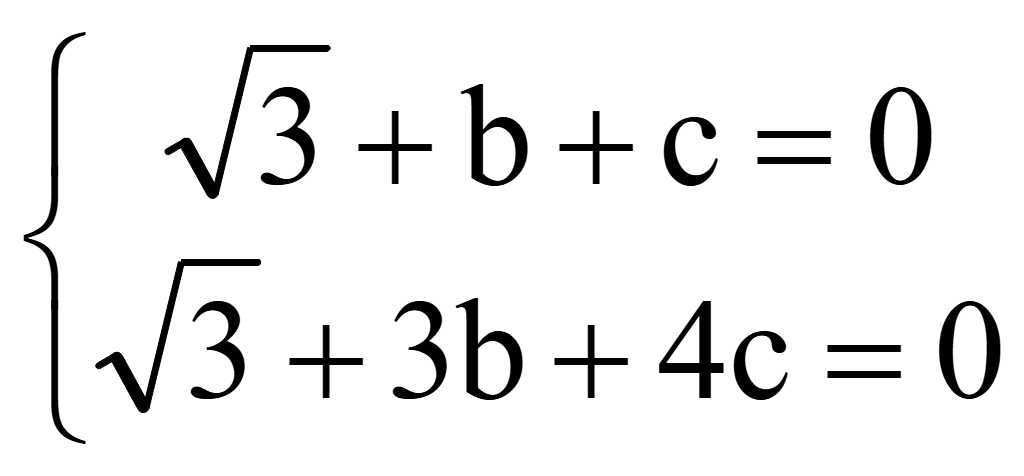
Можно из 1-го уравнения выразить b или c и подставить во 2-е уравнение.

Но мы решим систему методом исключения или методом Гаусса. Домножим 1-е уравнение на -3

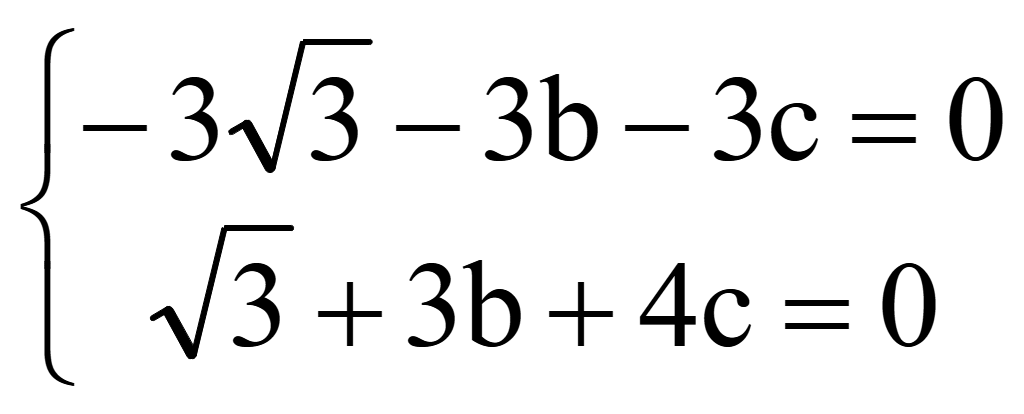
Сложим уравнения между собой

Подставим c в 1-е уравнение

Нормальный вектор плоскости BMN

Подставим a, b, c и получим уравнение плоскости BMN

Косинус угла между плоскостями

a₁x + b₁y + c₁z = 0

и

a₂x + b₂y + c₂z = 0

равен модулю косинуса угла между нормальными векторами = (a₁; b₁; c₁) и = (a₂; b₂; c₂) этих плоскостей

cos φ = |cos θ| =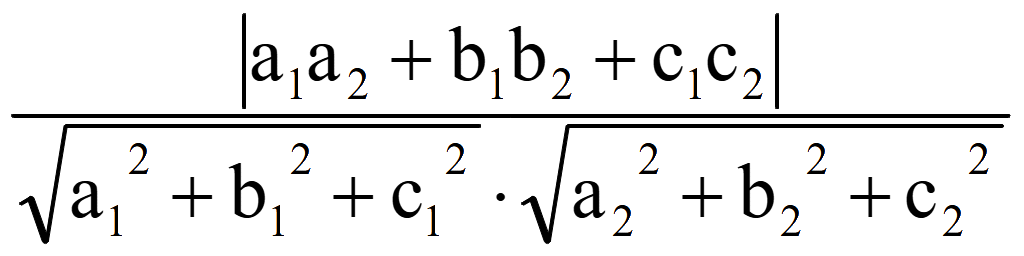

Подставляем координаты нормальных векторов и

cos φ = |cos θ| =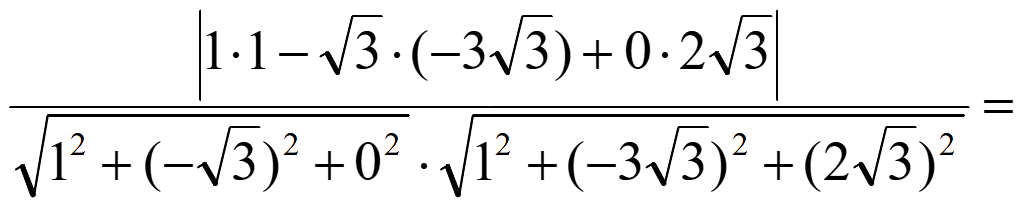

В решении, расписанном в Демо 2019, 2020, 2021 был указан ответ

но

Ответ: б) угол между плоскостями

41.2 Дополнительные задания к задаче № 14 ЕГЭ Демо 2019, 2020, 2021 проф

а) Найти угол между прямыми BN и AC.

б) Найти угол между прямой MN и плоскостью ABB₁.

в) Найти расстояние от точки C до плоскости BMN.

Решение

а) Найдем угол между прямыми BN и AC.

Определим направляющий вектор прямой BN. Координаты точек в ранее выбранной системе координат известны

B(0; 0; 0);

Вектор проведен из начала координат, поэтому координаты конца вектора (точки N) являются координатами вектора

Определим направляющий вектор прямой AC. Координаты точки A отличаются от координат точки только тем, что z = 0. Тогда координаты точек в ранее выбранной системе координат

C(0; 6; 0).

Координаты вектора равны разности координат конца вектора и начала

Косинус угла φ между прямыми BN и AC равен модулю косинуса угла θ между направляющими векторами и этих прямых

cos φ = |cos θ| =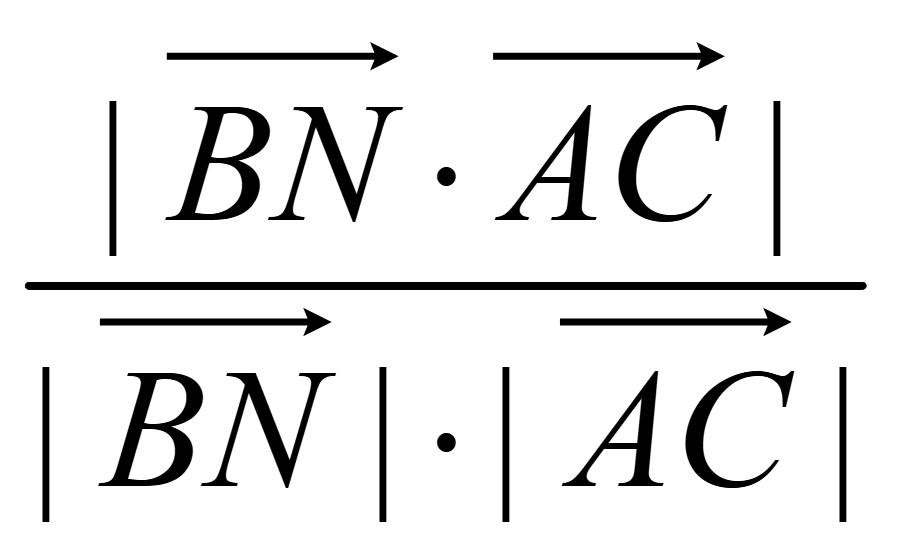

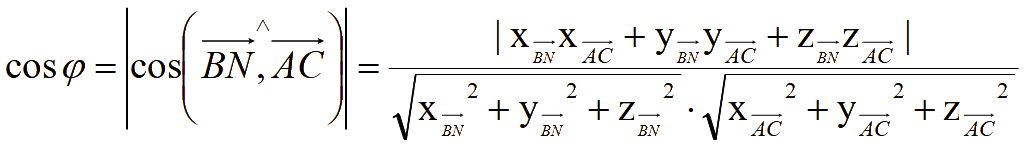
Отсюда угол между прямыми BN и AC

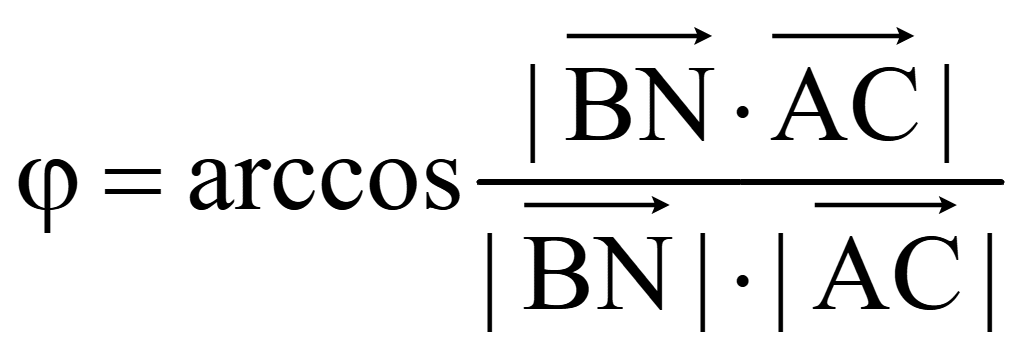
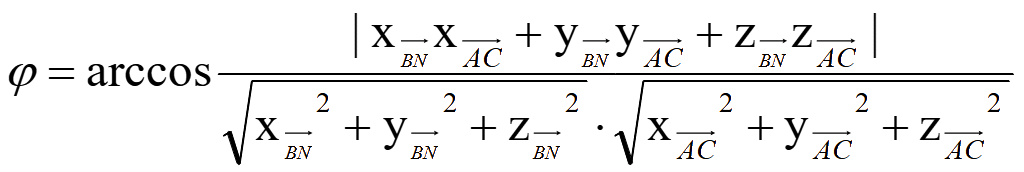
Подставим координаты направляющих векторов этих прямых

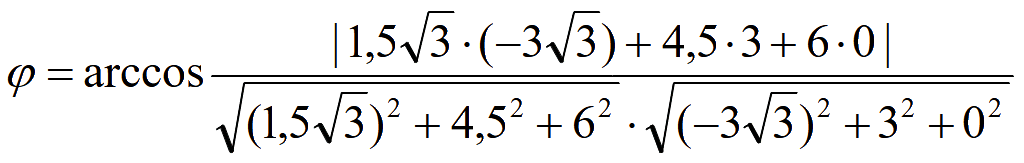
41.3 Задача № 14 (2) ЕГЭ Демо 2021

В правильной четырёхугольной пирамиде SABCD сторона АВ основания равна 16, а высота пирамиды равна 4. На рёбрах АВ, CD и AS отмечены точки M , N и K соответственно, причём AM = DN = 4 и AK = 3.

а) Докажите, что плоскости MNK и SBC параллельны.

б) Найдите расстояние от точки M до плоскости SBC.

Решение

Изобразим правильную четырехугольную пирамиду на виде сверху. Систему декартовых координат расположим так, чтобы плоскость SBC проходила через начало координат — точку B. Тогда ось Bz будет направлена вершиной из плоскости рисунка на нас.

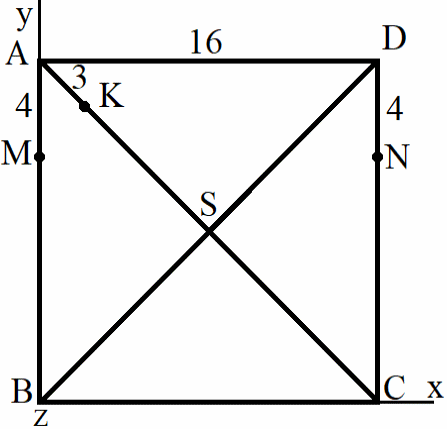
б) Найдем расстояние от точки M до плоскости SBC.

Длина отрезка

BM = AB – AM = 16 – 4 = 12.

Координаты точки

M(0; 12; 0).

Координаты точек плоскости SBC

S(8; 8; 4);

B(0; 0; 0);

C(16; 0; 0).

Определим общее уравнение плоскости SBC

ax + by + cz + d = 0.

Плоскость SBC проходит через начало координат, поэтому d = 0 и общее уравнение плоскости SBC упрощается

ax + by + cz = 0.

У точки C координата y равна нулю, поэтому соответствующий этой координате коэффициент принимаем равным единице

b = 1,

общее уравнение плоскости SBC снова упрощается

ax + y + cz = 0.

Подставим в общее уравнение плоскости координаты точек, образующих прямую, не проходящую через начало координат

S(8; 8; 4) и C(16; 0; 0).

Получим систему 2-х уравнений с неизвестными коэффициентами a и c

a8 + 8 + c4 = 0;

a16 + 0 + c0 = 0.

Из 2-го уравнения

a = 0.

Подставим в 1-е уравнение

0·8 + 8 + c4 = 0;

8 + 4c = 0.

Разделим обе части равенства на 4

2 + c = 0;

c = -2.

Получили

a = 0;

b = 1;

c = -2.

Общее уравнение плоскости SBC

y - 2z = 0

Вектор, перпендикулярный плоскости SBC (нормальный вектор)

(a; b; c) = (0; 1; -2).

Расстояние от точки M₀ (x₀; y₀; z₀) до плоскости, заданной уравнением

ax + by + cz + d = 0

определяется по формуле

ℓ =

Тогда расстояние от точки M₀ (x₀; y₀; z₀) до плоскости, заданной уравнением

y - 2z = 0

определится по формуле

ℓ =

ℓ =

Подставим координаты точки

M(0; 12; 0);

ℓ =

а) Докажем, что плоскости MNK и SBC параллельны.

Координаты точек плоскости MNK

M(0; 12; 0);

N(16; 12; 0).

Векторы и коллинеарны, поэтому их можно приравнять с помощью коэффициента k

= k

По условию длина вектора

= AK = 3.

Координаты точек

A(0; 16; 0);

S(8; 8; 4).

Координаты вектора равны разности соответствующих координат конца и начала вектора

= (8 - 0; 8 - 16; 4 - 0) = (8; -8; 4).

Длина вектора (x; y; z) равна корню квадратному из суммы квадратов его координат

Подставляем длины векторов

3 = k12.

k = 3/12 = 1/4 = 0,25.

= k = (k8; -k8; k4) = (8/4; -8/4; 4/4) = (2; -2; 1).

Координаты вектора равны разности соответствующих координат конца K(x; y; z) и начала вектора A(0; 16; 0)

= (x - 0; y - 16; z - 0) = (x; y - 16; z) = (2; -2; 1).

y - 16 = -2;

y = 16 – 2 = 14.

Координаты точки

K(2; 14; 1).

Если плоскости MNK и SBC параллельны, то координаты нормального вектора плоскости SBC (a; b; c) = (0; 1; -2) можно подставить в общее уравнение плоскости MNK

ax + by + cz + d = 0

После подстановки (a; b; c) = (0; 1; -2) получаем

0x + 1y - 2z + d = 0;

y - 2z + d = 0.

Подставим координаты точек M(0; 12; 0) и N(16; 12; 0) плоскости MNK, получим систему двух уравнений

12 - 2·0 + d = 0;

12 + d = 0.

Уравнения получились одинаковые, из них найдем

d = -12.

Получили уравнение плоскости, которая проходит через точки M и N и параллельна плоскости SBC

y - 2z - 12 = 0.

Подставляем координаты точки

K(2; 14; 1)

14 - 2·1 - 12 = 0.

Следовательно, плоскости MNK и SBC параллельны.

Ответ: б) расстояние от точки M до плоскости SBC

42 Решение задачи № 16 ЕГЭ Демо 2021 с помощью векторов

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Решение

Чертеж из ЕГЭ Демо приведен ниже.

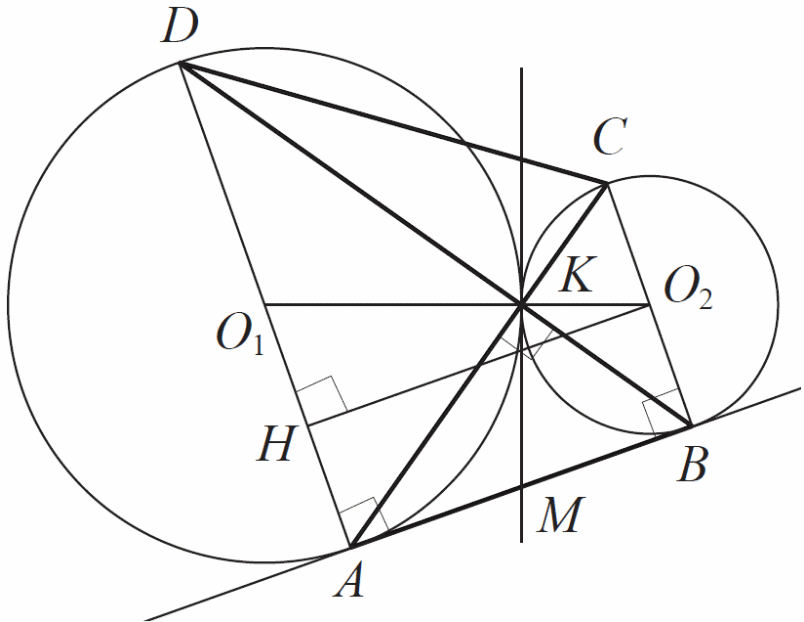
Нарисуем чертеж, принимая радиусы окружностей равными R = 4 и r = 1.

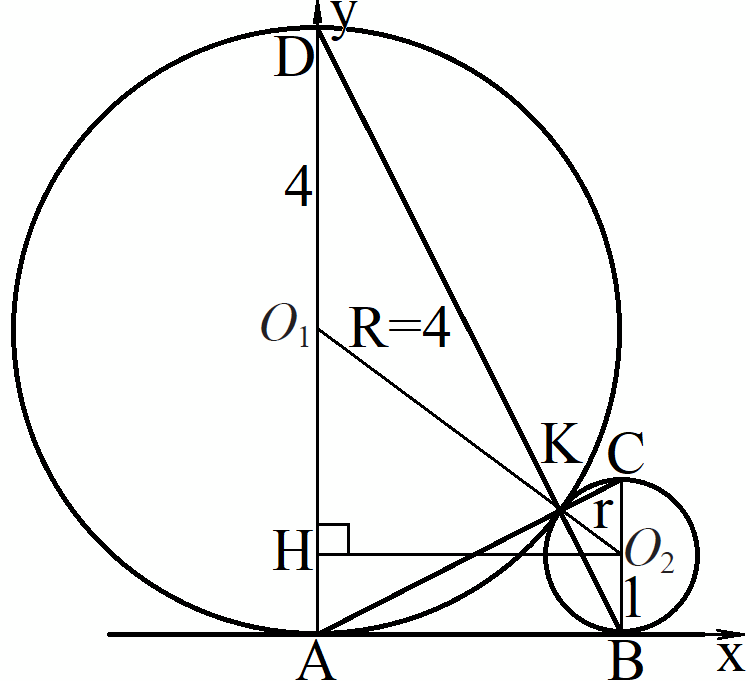
а) Докажем, что прямые AD и BC параллельны.

Выберем систему координат так, как показано на рисунке выше. Начало координат в точке A, ось x содержит прямую AB, ось у из точки A направим вертикально вверх. Координаты точек

A(0; 0);

O₁(0; 4).

Прямая AB по условию является касательной к окружностям, поэтому AB перпендикулярна радиусам AO₁ и BO₂. Из точки O₂ проведем прямую HO₂ параллельно прямой AB. Следовательно, прямая HO₂ также перпендикулярна радиусам AO₁ и BO₂. Значит, ABO₂H — прямоугольник, в котором

BO₂ = r = AH = 1.

В прямоугольном треугольнике O₁HO₂ угол O₁HO₂ = 90⁰, а гипотенуза

O₁O₂ = R + r = 4 + 1 = 5,

катет

HO₁ = AO₁ - AH = 4 - 1 = 3,

поэтому треугольник O₁HO₂ египетский и катет HO₂ = 4. Следовательно, координаты точек

B(4; 0);

O₂(4; 1).

Координаты вектора равны разности координат конца вектора O₂(4; 1) и начала O₁(0; 4)

= (4 - 0; 1 - 4) = (4; -3).

= O₁O₂ = 5.

= O₁K = R = 4.

Векторы и лежат на одной прямой, следовательно, они коллинеарны, поэтому их можно приравнять с помощью коэффициента k

= k = (4k; -3k);

Модули коллинеарных векторов также можно приравнять с помощью коэффициента k

= k

Отсюда коэффициент k

k =

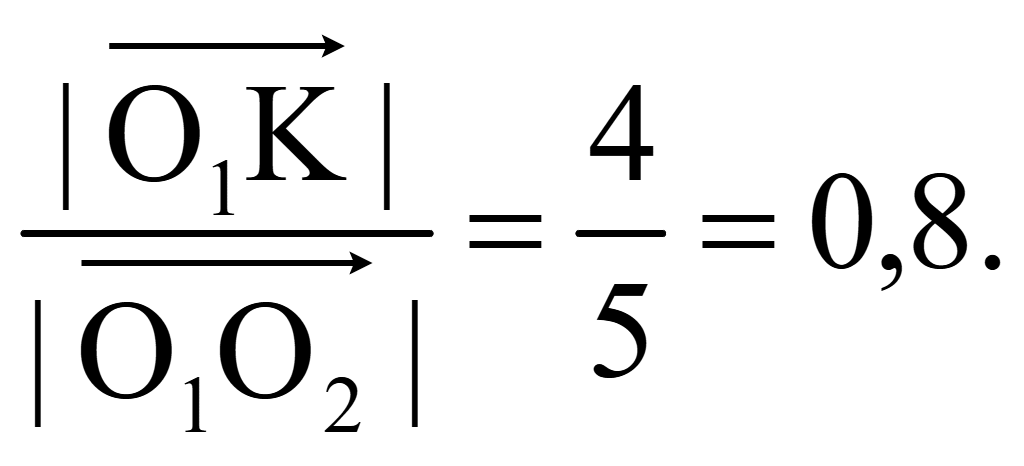
Координаты вектора в случае его откладывания из начала координат

= (4k; -3k) = (4·0,8; -3·0,8) = (3,2; -2,4).

Но координаты точки

O₁(0; 4),

поэтому координаты конца вектора (точки K), в случае откладывания вектора из точки O₁(0; 4), увеличатся на величину соответствующих координат точки O₁(0; 4)

K = (3,2 + 0; -2,4 + 4) = (3,2; 1,6).

Координаты вектора, проведенного из точки A, являющейся началом координат, равны координатам конца вектора

= (3,2; 1,6).

Координаты вектора равны разности координат конца вектора K (3,2; 1,6) и начала B(4; 0)

= (3,2 - 4; 1,6 - 0) = (-0,8; 1,6).

Скалярное произведение векторов в координатах равно сумме произведений соответствующих координат

· = 3,2·(-0,8) + 1,6·1,6 = 0.

Скалярное произведение векторов · равно 0, следовательно, векторы и перпендикулярны. Значит и коллинеарные им вектора и перпендикулярны. Следовательно, треугольники AKD и BKC прямоугольные. Следовательно, AD и BC – диаметры окружностей, проходящие через центры окружностей O₁ и O₂. По условию прямая AB касается первой окружности в точке A, а второй — в точке B. Следовательно, диаметры окружностей AD и BC, а также одноименные прямые AD и BC параллельны, что и требовалось доказать.

б) Найдем площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Векторы и перпендикулярны, следовательно, треугольник AKB прямоугольный. Площадь прямоугольного треугольника равна половине произведения катетов

Длина вектора = (3,2; 1,6):

Длина вектора = (-0,8; 1,6)

Подставим и найдем площадь треугольника

Ответ: S_∆AKB = 3,2 ед².

43 Решение геометрических задач с помощью векторов

Порядок решения геометрических задач с помощью векторов:

1. Выбрать удобное расположение трехмерной системы координат.

2. Определить координаты точек, выбирая масштаб единичных отрезков так, чтобы как можно больше координат точек были равны единице. Обычно требуется определить координаты двух точек, задающих прямую или трех точек, определяющих плоскость.

3. По координатам точек определить направляющий вектор прямой или нормальный вектор плоскости.

4. Решить задачу координатным методом.

44 Векторы в аналитической геометрии высшей школы

44.1 Взаимное расположение прямых в пространстве

Возможные варианты взаимного расположения 2-х прямых в пространстве:

1. Прямые не лежат в одной плоскости, следовательно, скрещиваются.

2. Прямые лежат в одной плоскости, поэтому могут:

   1. Пересекаться.

   2. Совпадать.

   3. Быть параллельны.

Если одна прямая задана двумя точками M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂), то направляющий вектор этой прямой имеет координаты

= (x₂ - x₁; y₂ - y₁; z₂ - z₁).

Если вторая прямая также задана двумя точками M₃(x₃; y₃; z₃) и M₄(x₄; y₄; z₄), то направляющий вектор этой прямой имеет координаты

= (x₄ - x₃; y₄ - y₃; z₄ - z₃).

Проведем третий вектор, связывающий две точки, лежащие на разных прямых, например, с координатами

= (x₃ - x₁; y₃ - y₁; z₃ - z₁).

Если векторы , и не компланарны, то прямые скрещиваются. Смешанное произведение не компланарных векторов не равно нулю

· · ≠ 0.

Если смешанное произведение векторов равно нулю

· · = 0,

то прямые лежат в одной плоскости.

Если не выполняется условие коллинеарности векторов = k· , то прямые пересекаются. В противном случае направляющие векторы коллинеарны, а прямые параллельны или совпадают.

Чтобы убедиться в совпадении этих прямых, можно в каноническое уравнение первой прямой

подставить координаты одной точки, задающей вторую прямую, например M₃(x₃; y₃; z₃). Если отношения

равны, то прямые имеют по крайней мере одну общую точку M₃, следовательно, совпадают.

Если отношения в каноническом уравнении не равны, то точка второй прямой не принадлежит первой прямой, следовательно, прямые параллельны.

44.2 Деление отрезка в заданном отношении

μ(x - x₁) = λ(x₂ – x)

μx - μx₁ = λx₂ – λx;

μx + λx = λx₂ + μx₁;

x(μ + λ) = λx₂ + μx₁;

μ(y – y₁) = λ(y₂ – y)

При A(1; 1; 1) и B(3; 3; 3), μ = 3 и λ = 1

μ = 1 и λ = 3

μ = -1 и λ = 3

μ = 1 и λ = -3

μ = 3 и λ = -1

44.3 Координаты вектора в ортонормированном базисе

Координаты вектора или проекции вектора на оси координат

x = | |cosα,

где α — угол между вектором и осью x.

y = | |cosβ,

где β — угол между вектором и осью y.

z = | |cosγ,

где γ — угол между вектором и осью z.

x = · ;

y = · ;

z = · .

Разложение вектора в данном базисе

= x + y + z .

44.4 Правая и левая тройка векторов

Тройкой векторов , , называются некомпланарные векторы в указанном порядке, построенные из одной точки.

Единичные векторы , , системы координат xyz всегда образуют тройку векторов.

Если из конца вектора смотреть на плоскость, в которой лежат векторы и , то если поворот от вектора к вектору по кратчайшему пути совершается против часовой стрелки, то тройку векторов , , называют правой, если кратчайший поворот от к совершается по часовой стрелки, то тройку векторов , , называют левой.

Правая тройка векторов , , или , , (системы координат xyz) ориентирована также, как большой, указательный и средний пальцы правой руки.

Левая тройка векторов , , или , , ориентирована также, как большой, указательный и средний пальцы левой руки.

44.5 Векторное произведение векторов

Векторное произведение двух векторов – это вектор, перпендикулярный каждому из двух заданных векторов. Три вектора , , расположены относительно друг друга также как , , . Длина вектора равна произведению длин заданных векторов на синус угла между ними

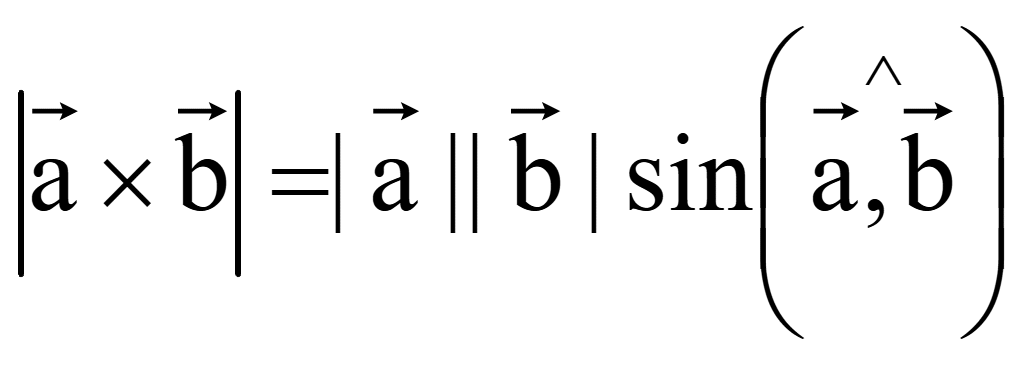
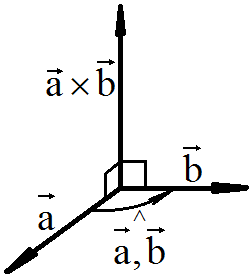
Модуль векторного произведения векторов равен площади параллелограмма, образованного векторами и , а также параллельными им отрезками

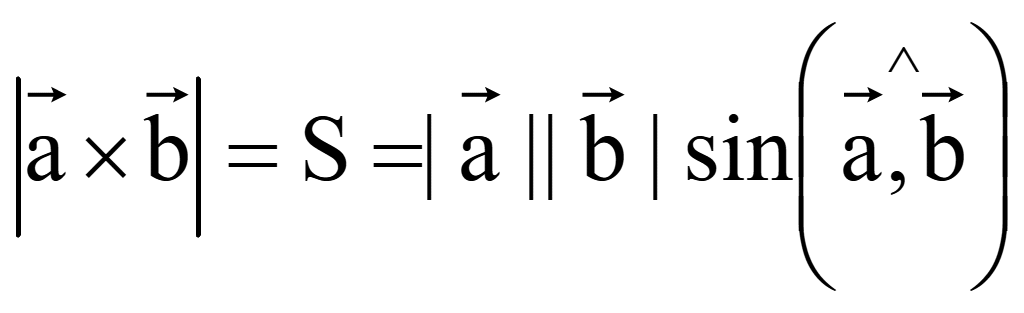
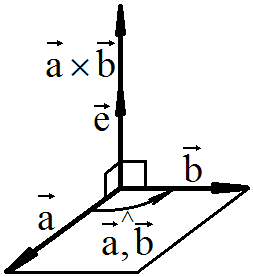
Векторное произведение векторов равно произведению площади S параллелограмма, построенного на векторах и , умноженной на единичный вектор в направлении вектора

Если = 0⁰, то векторы сонаправлены и 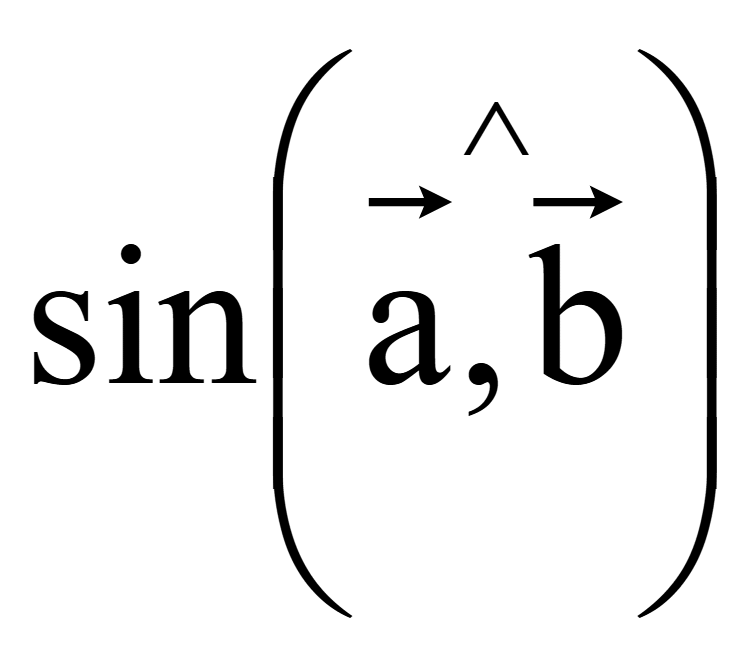= sin 0⁰ = 0, следовательно, векторное произведение двух сонаправленных векторов равно нулевому вектору

.

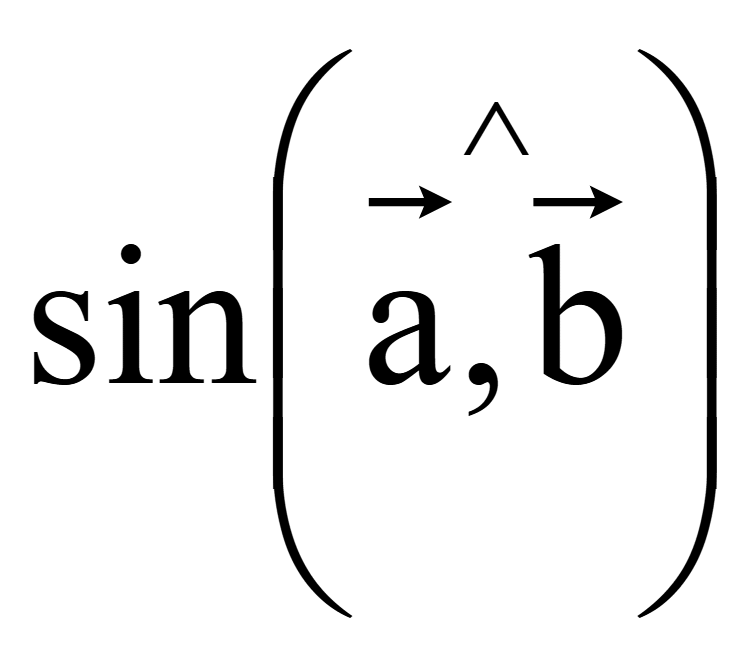Если угол между векторами 0 < < 90⁰, то синус угла между такими векторами больше нуля > 0, следовательно векторное произведение двух таких векторов дает вектор со знаком "плюс". При увеличении угла между векторами от 0⁰ до 90⁰ 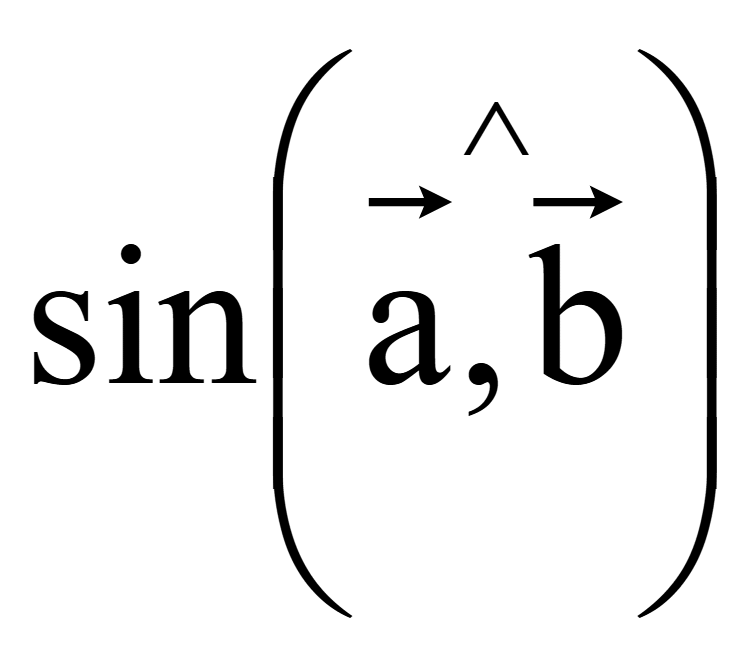также возрастает, поэтому увеличивается и длина вектора .

Если два ненулевых векторы перпендикулярны = 90⁰, то их векторное произведение дает вектор, длина которого равна произведению длин (модулей) заданных векторов , так как sin 90⁰ = 1.

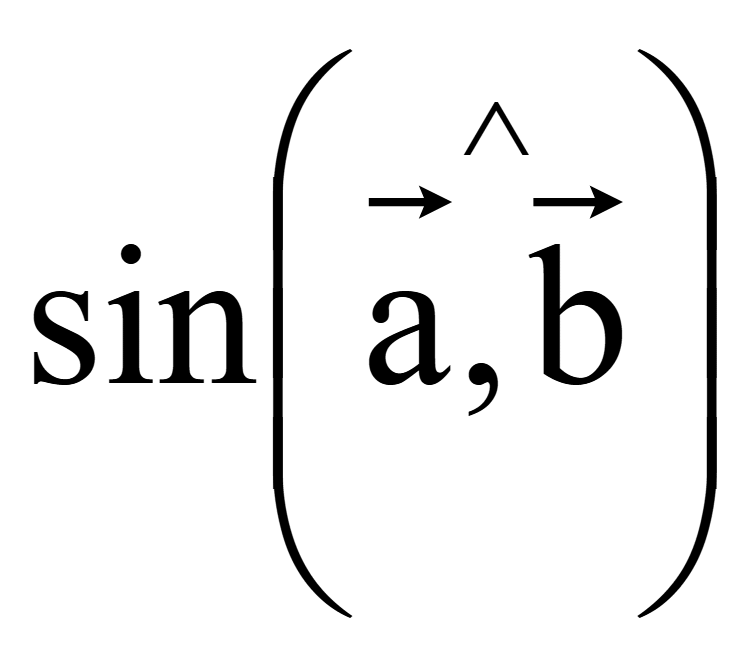Если , то синус угла между такими векторами больше нуля > 0, следовательно векторное произведение двух таких векторов дает вектор со знаком "плюс". При увеличении угла между векторами от 90⁰ до 180⁰ 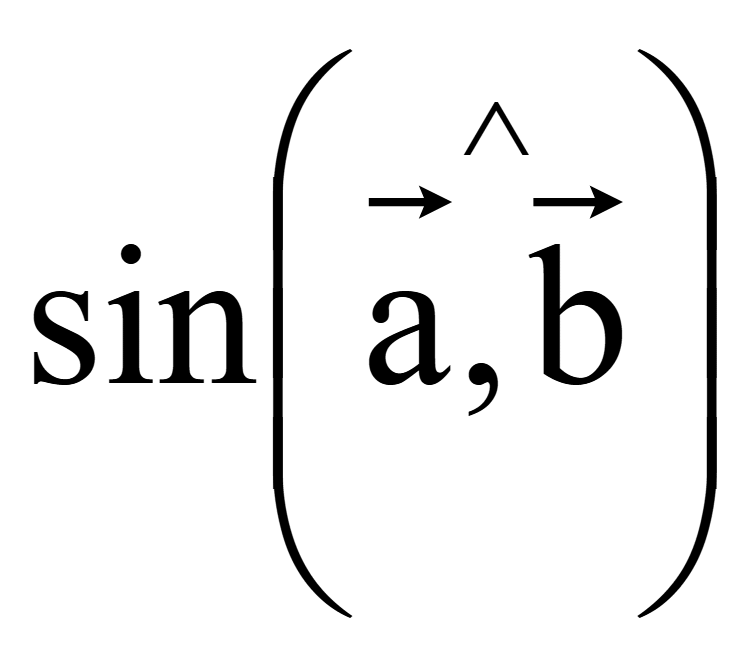уменьшается, поэтому уменьшается и длина вектора .

При увеличении угла между двумя векторами синус угла между ними 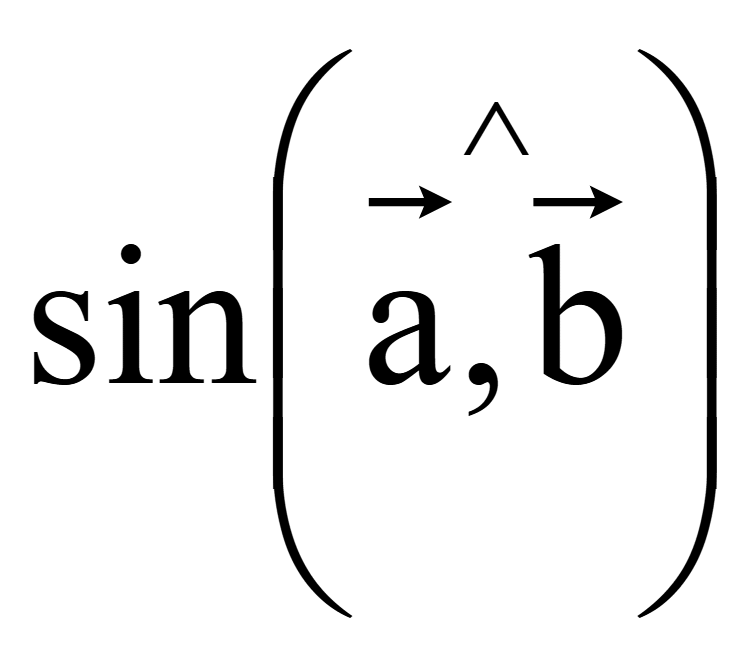уменьшается и достигает минимального значения при = 180⁰, когда векторы противоположно направлены . Так как sin 180⁰ = 0, то векторное произведение двух противоположно направленных векторов равно нулевому вектору

.

В итоге, векторное произведение двух сонаправленных или противоположно направленных, то есть коллинеарных векторов равно нулевому вектору или нулю

.

= 0.

Векторное произведение двух перпендикулярных векторов дает вектор, длина которого равна произведению длин (модулей) заданных векторов

.

Векторное произведение двух векторов всегда дает вектор со знаком "плюс". Это значит, что взаимная ориентация трех векторов , , всегда такая же как и взаимная ориентация единичных векторов , , и не зависит от угла между заданными векторами и .

Векторное произведение двух векторов = (x₁; y₁; z₁) и = (x₂; y₂; z₂) можно определить с помощью символического определителя третьего порядка

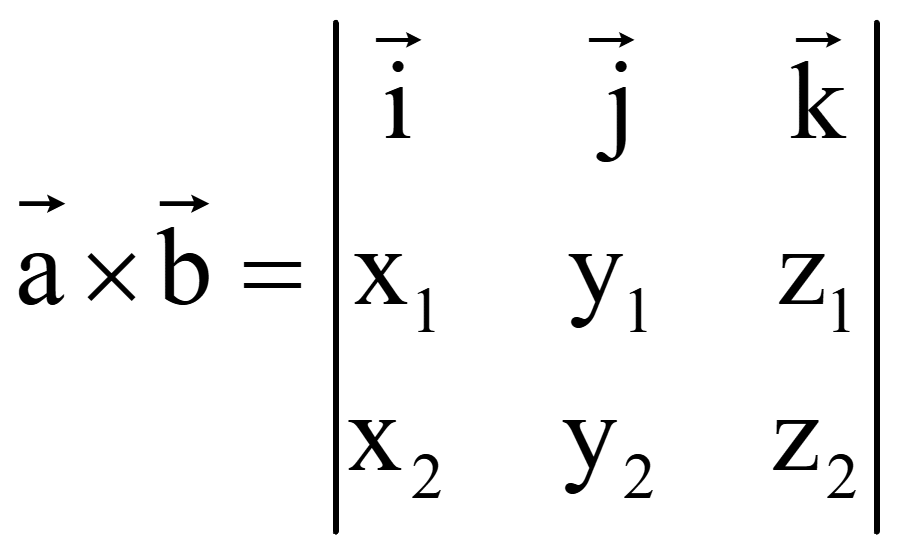
Разложение определителя третьего порядка по элементам первой строки

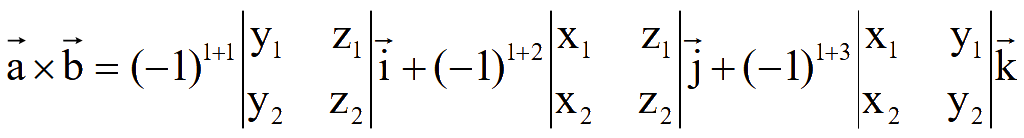
дает формулу вычисления координат вектора, полученного в результате векторного произведения двух векторов

,

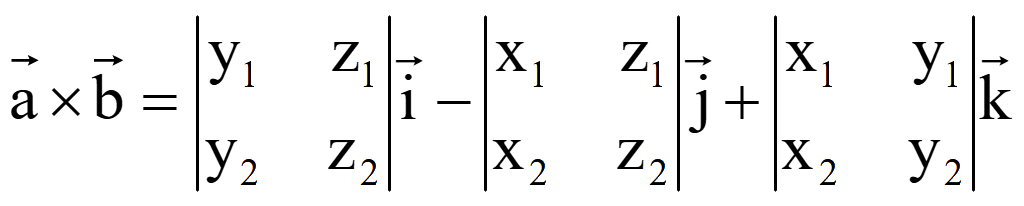Координаты вектора :

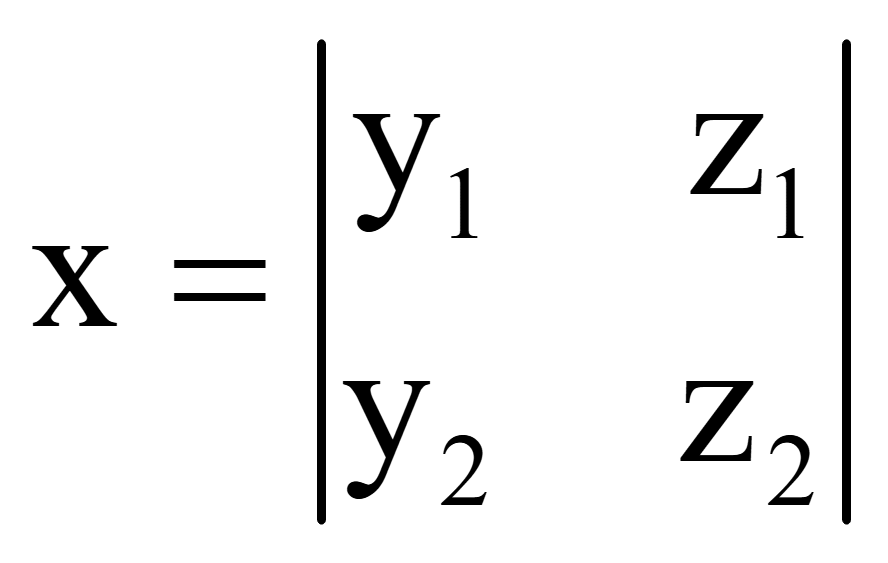
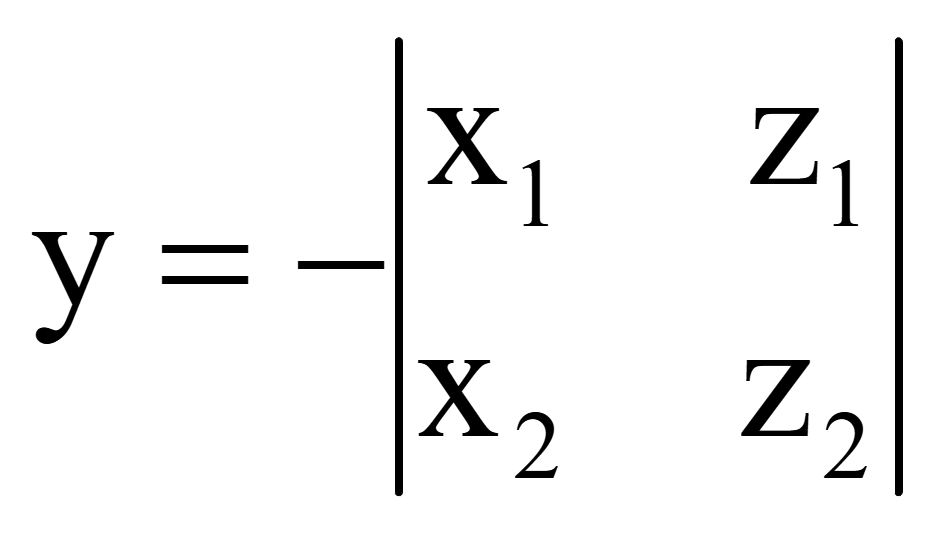
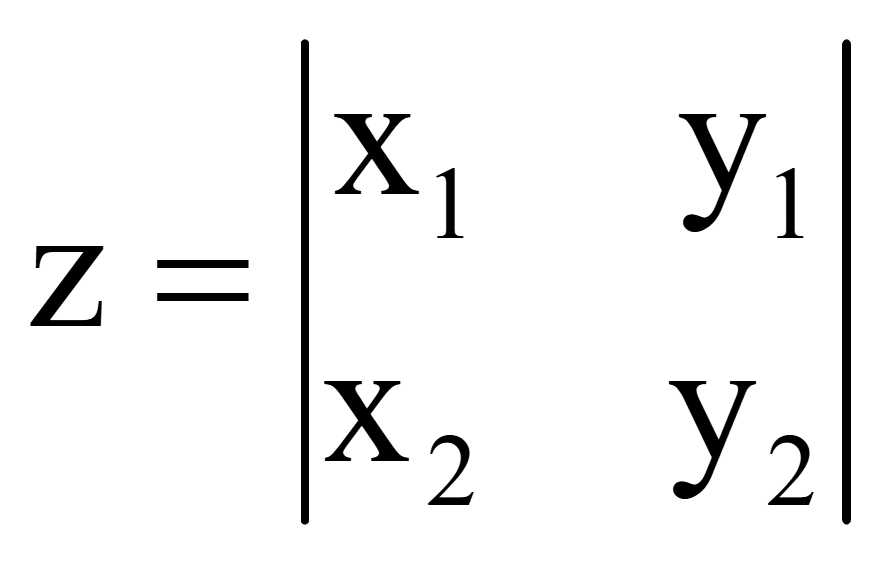
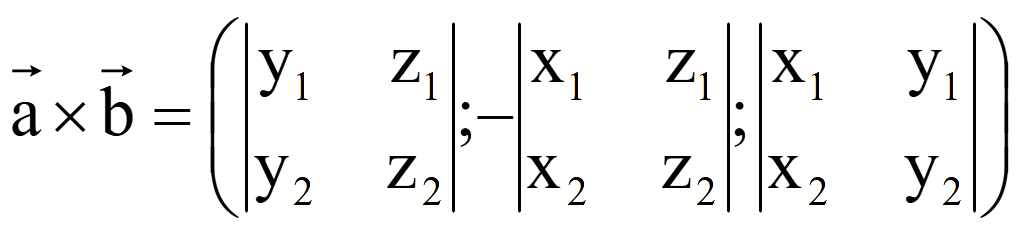
Миноры являются определителями второго порядка, поэтому вычисляются следующим образом

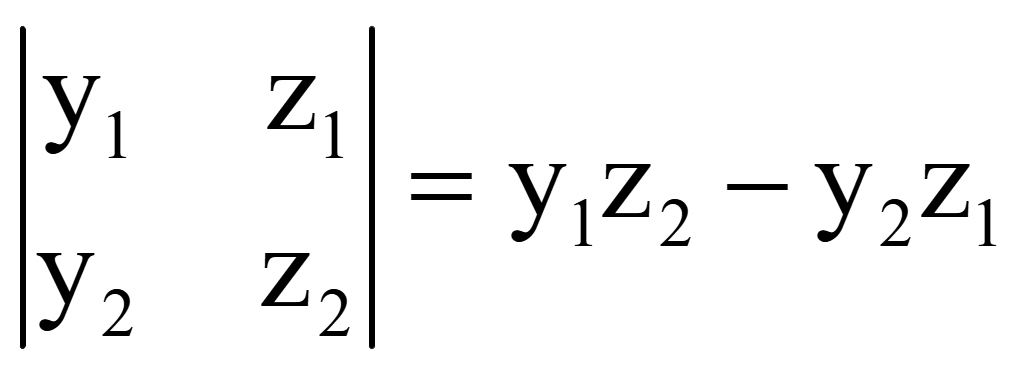
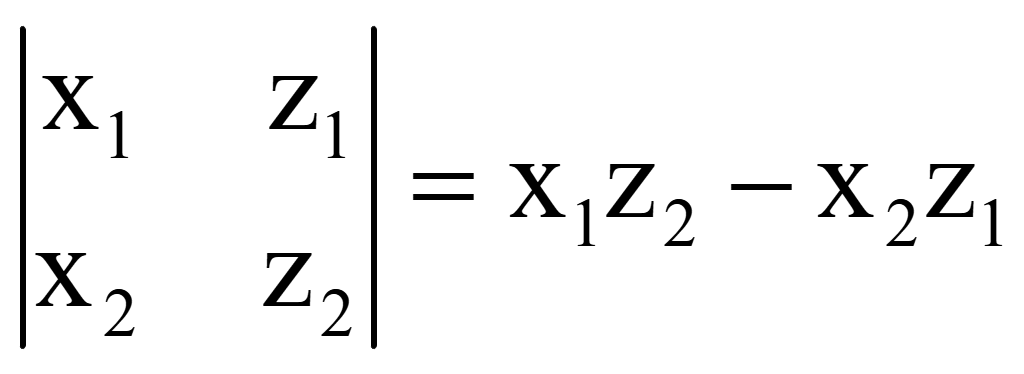
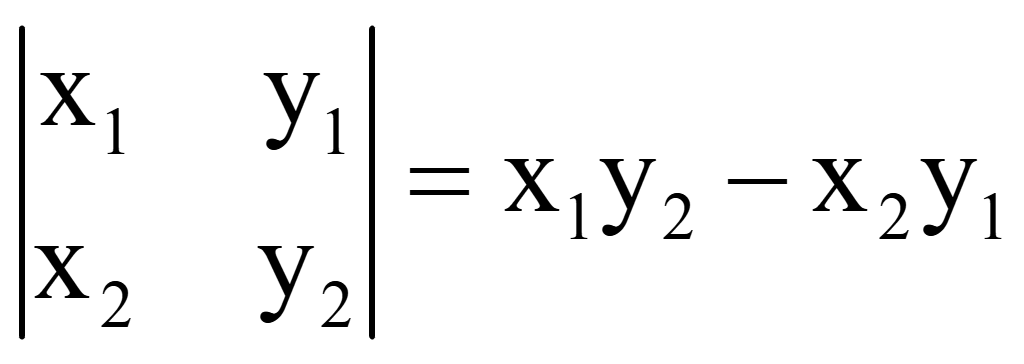
Векторное произведение двух векторов

Координаты вектора

Площадь параллелограмма, образованного двумя векторами = (x₁; y₁; z₁) и = (x₂; y₂; z₂), определяется по формуле

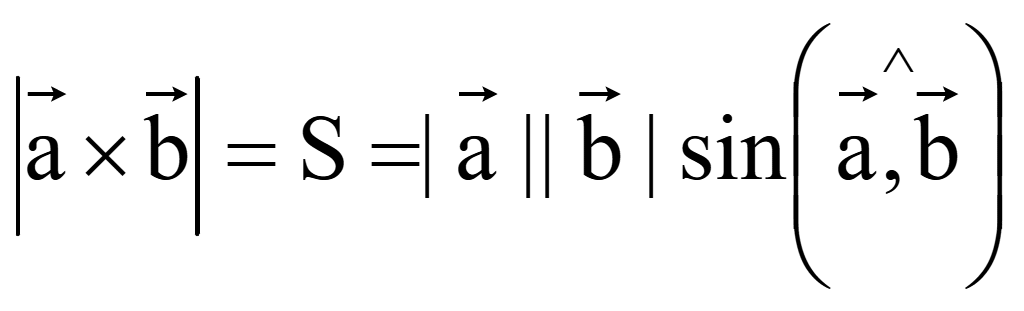
Модуль вектора

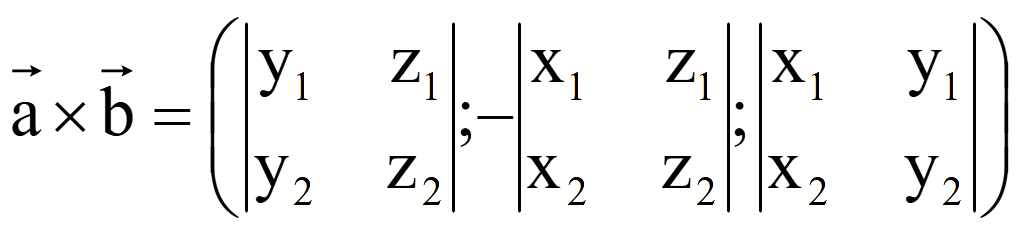
равен корню квадратному из суммы квадратов его координат

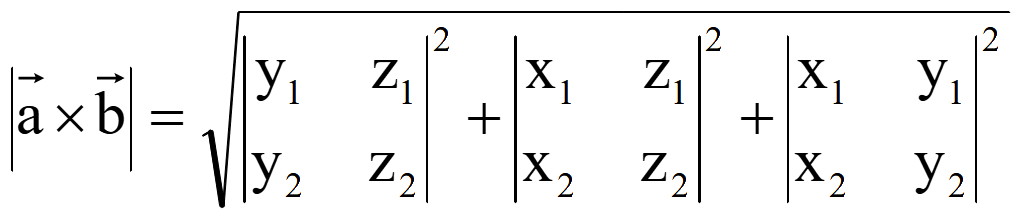
Поэтому площадь параллелограмма, образованного двумя векторами = (x₁; y₁; z₁) и = (x₂; y₂; z₂)

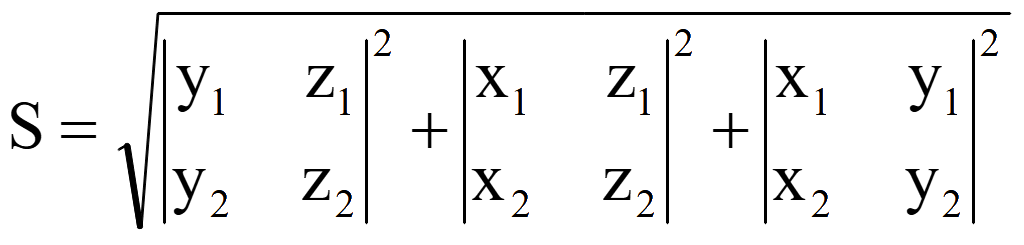
Площадь параллелограмма, образованного векторами и равна корню квадратному из суммы квадратов координат вектора

.

Площадь ∆ABC равна половине площади параллелограмма ABDC

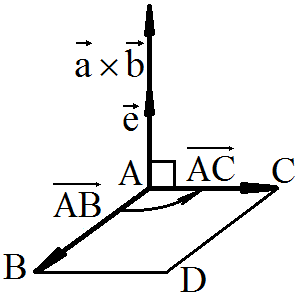
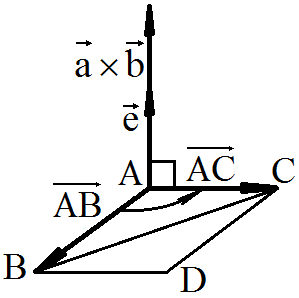
Если два вектора имеют координаты = (x₁; y₁; z₁) и = (x₂; y₂; z₂), то

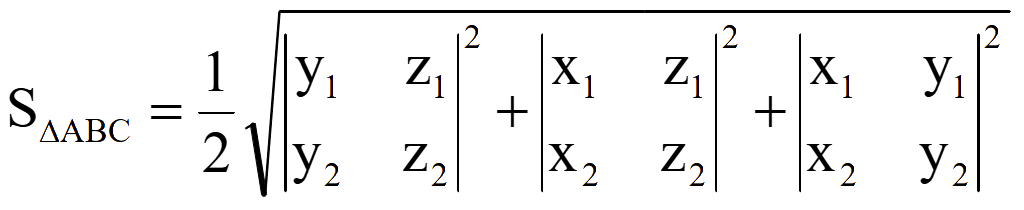
Модуль векторного произведения векторов равен площади параллелограмма, образованного векторами и , а также параллельными им отрезками

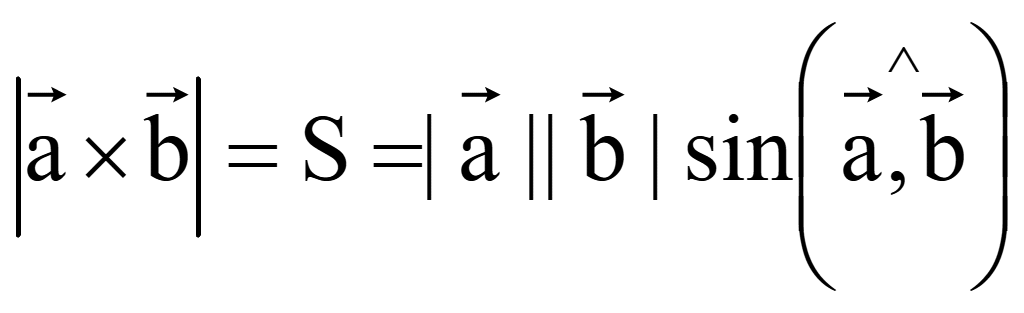
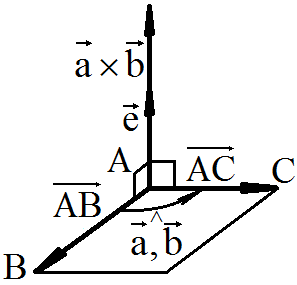
Задача. Вычислить векторное произведение двух векторов = (0; 3; 4) и = (-1; 0; 2).

Решение

Векторное произведение векторов запишем в виде определителя третьего порядка

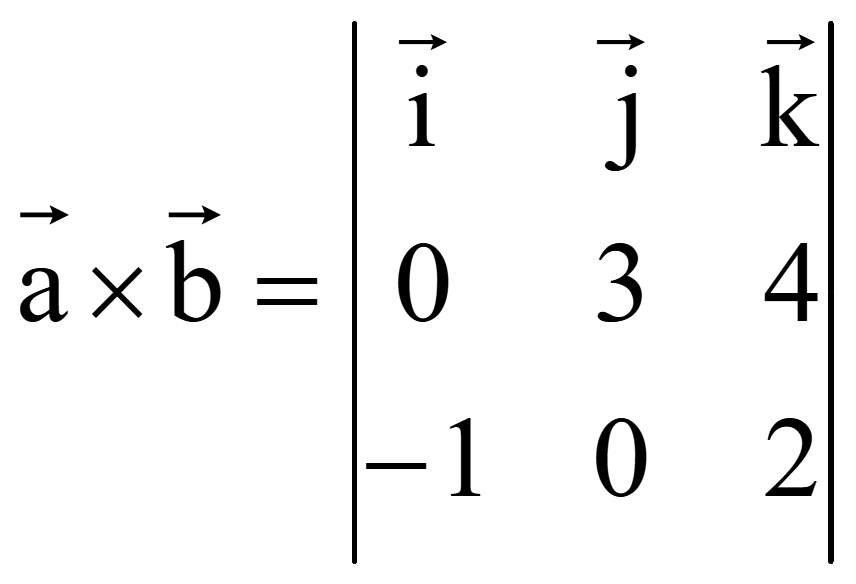
Для вычисления определителя третьего порядка разложим его по элементам первой строки

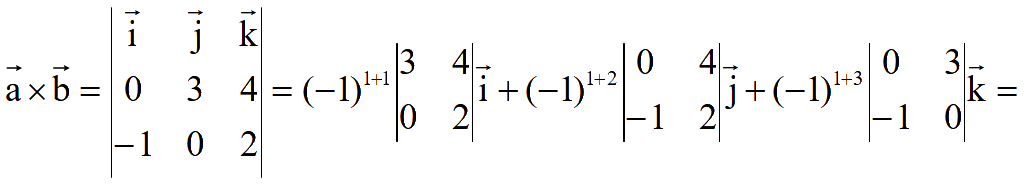
Вектор имеет координаты

= (6; -4; 3).

Задача. Вычислить векторное произведение двух векторов = (1; 0; 0) и = (0; 1; 0).

Решение

Вектор = (1; 0; 0) лежит на оси Ox, вектор = (0; 1; 0) лежит на оси Oy.

Векторное произведение векторов запишем в виде определителя третьего порядка

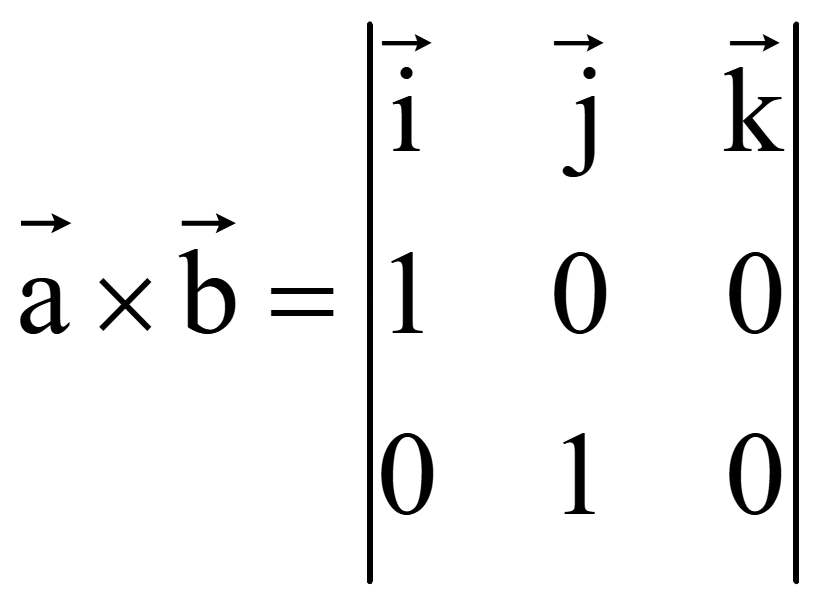
Для вычисления определителя третьего порядка разложим его по элементам первой строки

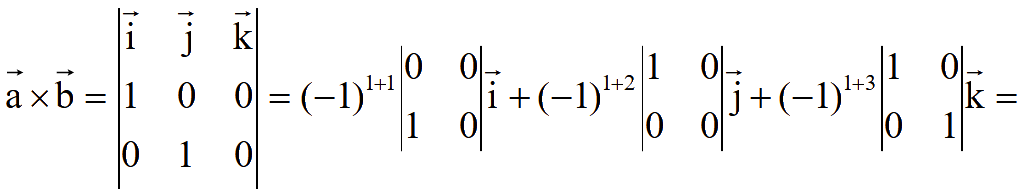
Вектор лежит на оси Oz, имеет координаты

= (0; 0; 1).

Задача. Вычислить векторное произведение двух векторов = (1; 2; 3) и = (2; 4; 6).

Решение

1 способ

Векторное произведение векторов запишем в виде определителя третьего порядка

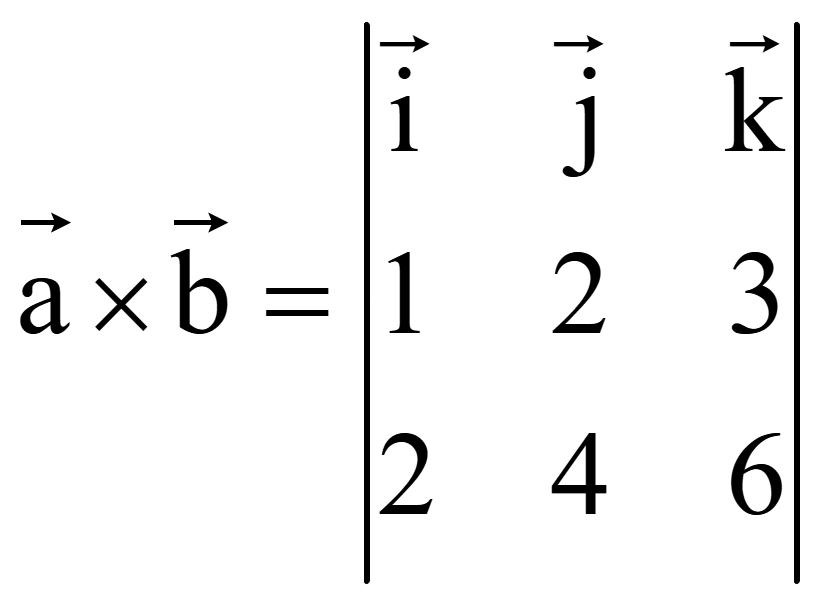
Для вычисления определителя третьего порядка разложим его по элементам первой строки

Вектор нулевой

= (0; 0; 0),

следовательно векторы и коллинеарные.

2 способ

Координаты вектора в 2 раза больше координат вектора , следовательно

= 2 .

Следовательно, векторы и коллинеарные, а точнее сонаправленные. Значит их векторное произведение равно нулю.

Задача. Вычислить векторное произведение двух векторов = (1; 1; 1) и = (-3; -3; -3).

Решение

Координаты вектора получаются из координат вектора путем умножения на коэффициент -3, следовательно

= -3 .

Следовательно, векторы и коллинеарные, а точнее противоположно направленные. Значит их векторное произведение равно нулю.

Задача. Вычислить векторное произведение двух векторов = (1; 1; 1) и = (-1; 1; 1).

Решение

Векторное произведение векторов запишем в виде определителя третьего порядка

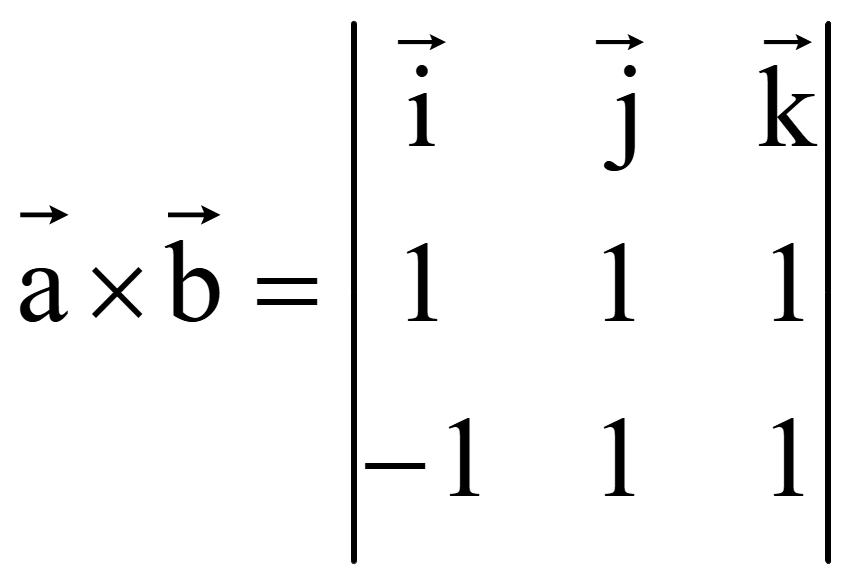
Для вычисления определителя третьего порядка разложим его по элементам первой строки

Координаты вектора

= (0; -2; 2).

Площадь параллелограмма, образованного векторами и равна корню квадратному из суммы квадратов координат вектора = (0; -2; 2)

.

44.6 Смешанное произведение трех векторов

Смешанным произведением трех векторов , и называется их векторно-скалярное произведение:

· · = [ ]· = ·[ ].

Смешанное произведение дает число, полученное в результате векторного произведения векторов , скалярно умноженного на вектор или скалярного произведения вектора на вектор, полученный в результате векторного произведения .

Смешанное произведение компланарных векторов равно нулю

· · = 0.

Смешанное произведение не компланарных векторов не равно нулю

· · ≠ 0.

Перестановка местами двух векторов приводит к смене знака смешанного произведения

= = = - = - = - .

Если даны координаты трех векторов = (x₁; y₁; z₁), = (x₂; y₂; z₂) и = (x₃; y₃; z₃), то смешанное произведение этих векторов вычисляется через определитель третьего порядка

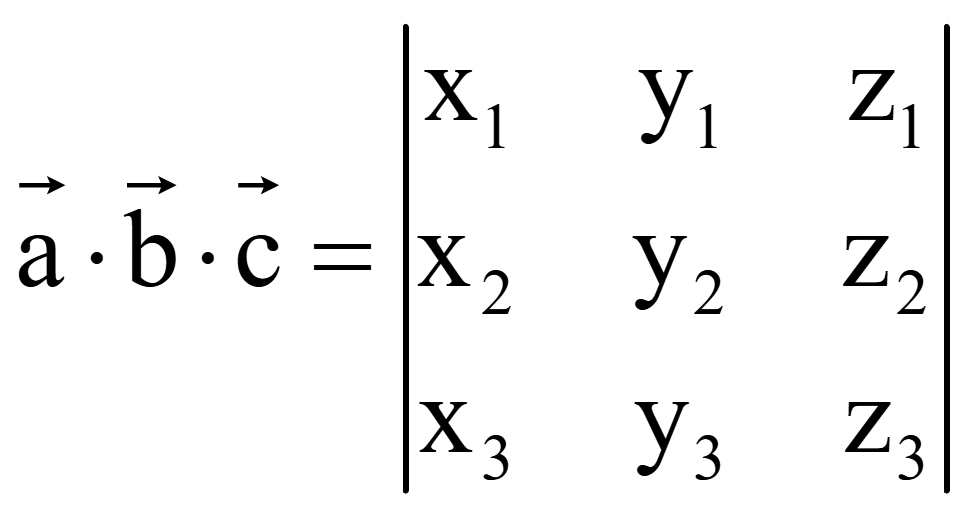
Разложение определителя третьего порядка по элементам первой строки

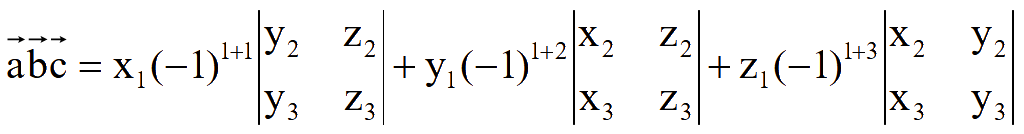
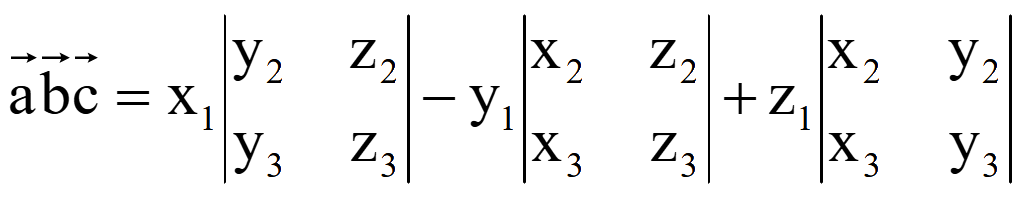
Геометрически модуль смешанного произведения трех векторов равен объему параллелепипеда, образованного векторами , и

V = | |

Модуль смешанного произведения трех векторов позволяет перемножать их в произвольном порядке.

Модуль обозначим словом mod, тогда объем параллелепипеда

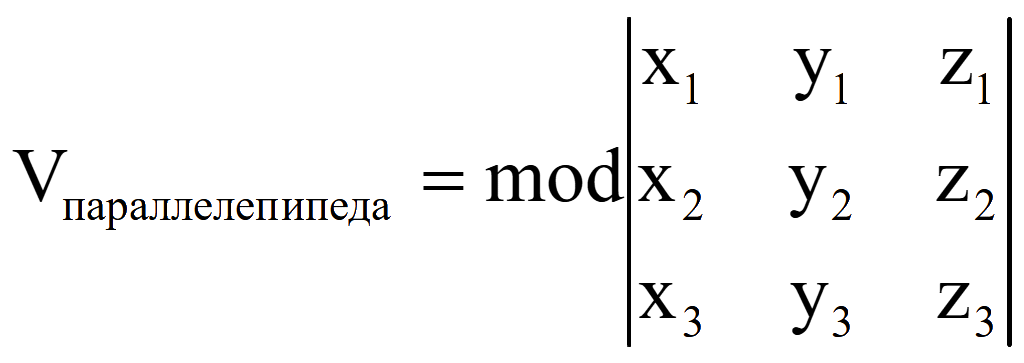
Если известны 4 точки параллелепипеда M₁ = (x₁; y₁; z₁), M₂ = (x₂; y₂; z₂), M₃ = (x₃; y₃; z₃) и M₄ = (x₄; y₄; z₄), то для нахождения объема найдем координаты 3-х векторов, образующих параллелепипед

= (x₂ - x₁; y₂ - y₁; z₂ - z₁)

= (x₃ - x₁; y₃ - y₁; z₃ - z₁)

= (x₄ - x₁; y₄ - y₁; z₄ - z₁)

Объем параллелепипеда, образованного векторами , и равен модулю смешанного произведения этих векторов

V = | · · |

Объем параллелепипеда

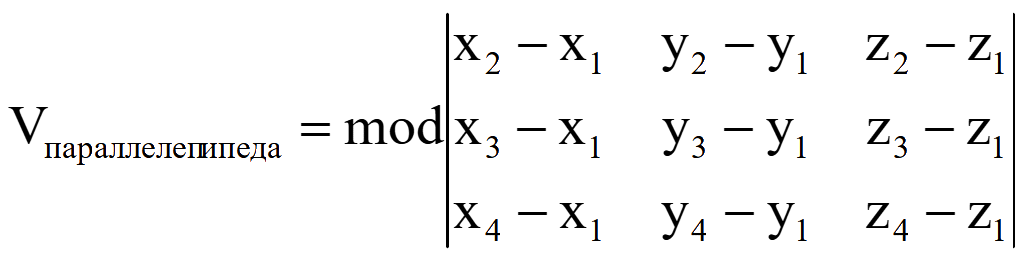
Объем пирамиды

с любой фигурой в основании, в том числе и с параллелограммом или треугольником в основании.

Объем параллелепипеда

Объем пирамиды, образованной векторами , и с параллелепипедом в основании равен 1/3 модуля смешанного произведения этих векторов

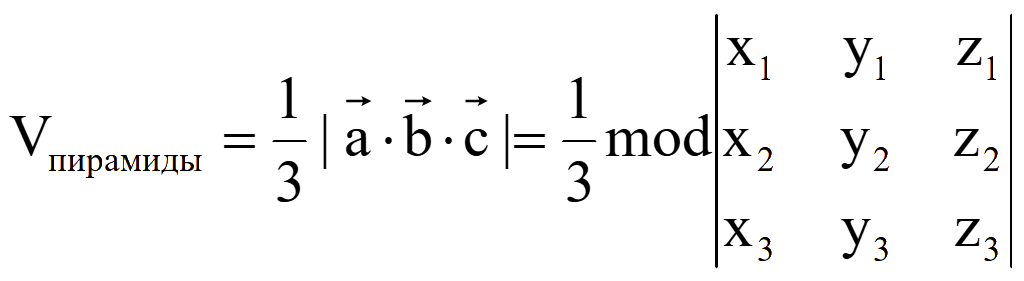
Объем пирамиды, заданной 4-мя точками M₁ = (x₁; y₁; z₁), M₂ = (x₂; y₂; z₂), M₃ = (x₃; y₃; z₃) и M₄ = (x₄; y₄; z₄)

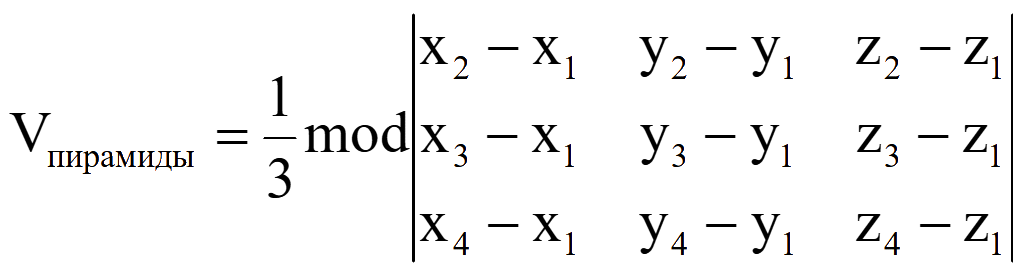
Диагональ параллелограмма делит его на два равных треугольника, поэтому объем пирамиды в основании, которой такой треугольник, будет в 2 раза меньше объема пирамиды, в основании которой исходный параллелограмм. Пирамида, состоящая из 4-х треугольников, называется тетраэдром.

Объем тетраэдра, образованного векторами , и равен 1/6 модуля смешанного произведения этих векторов

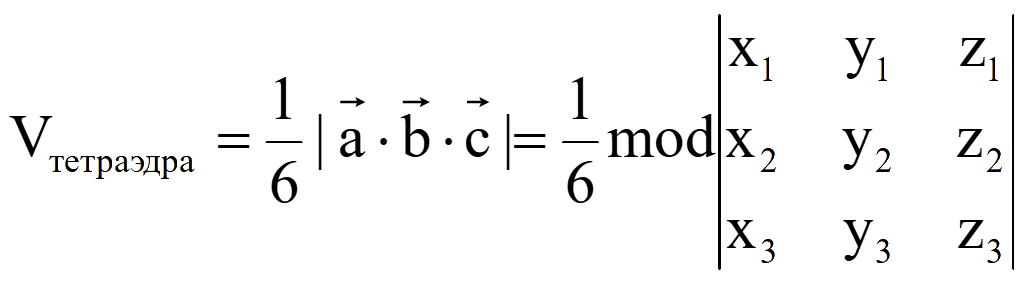
Объем тетраэдра, заданного 4-мя вершинами M₁ = (x₁; y₁; z₁), M₂ = (x₂; y₂; z₂), M₃ = (x₃; y₃; z₃) и M₄ = (x₄; y₄; z₄)

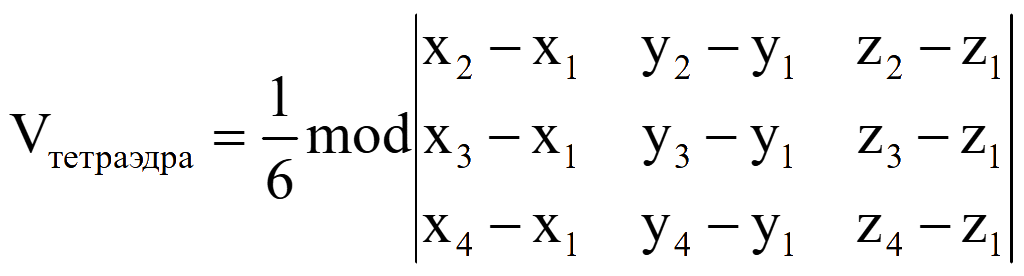
Задача. Найти объем параллелепипеда, объем пирамиды с параллелограммом в основании и объем тетраэдра, построенных на векторах = (-1; -2; 3), = (2; 1; -3) и = (-1; -3; 2).

Решение

Объем параллелепипеда, образованного векторами , и равен модулю смешанного произведения этих векторов

V = | |

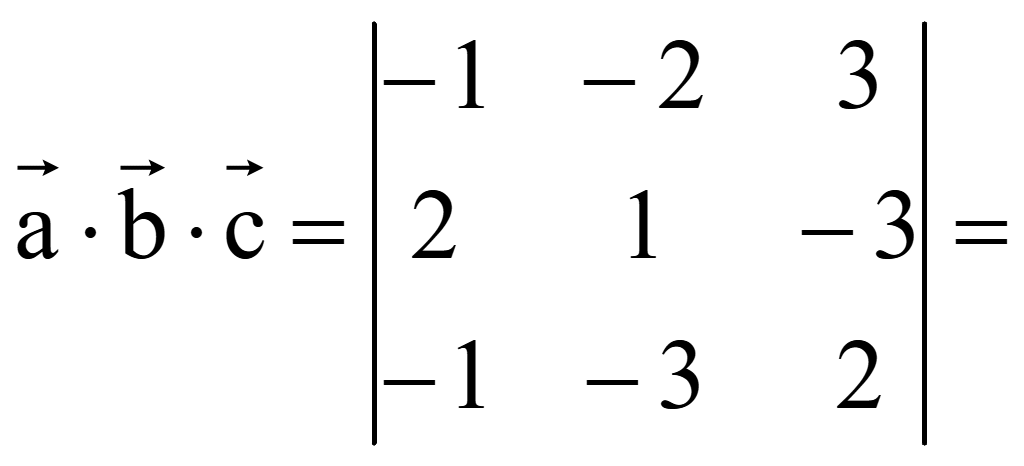
= -(1·2 - (-3)·(-3)) + 2·(2·2 - (-1)·(-3)) + 3·(2·(-3) - (-1)·1) =

= -(2 - 9) + 2·(4 - 3) + 3·(-6 + 1) = 7 + 2 - 15 = -6.

Объем параллелепипеда

V = |-6| = 6 ед³.

Объем пирамиды с параллелограммом в основании

= 2 ед³.

Объем тетраэдра

= 1 ед³.

45 Список литературы

1. Геометрия. 7-9 классы : учеб. для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.] - М. : Просвещение, 2021. - 384 с.

2. Геометрия. 10-11 класс. Учебник. Базовый и углублённый уровни / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.] - М. : Просвещение, 2021. - 288 с.

Векторы на плоскости и в пространстве веб-страницы: 1 2 3

© 03.06.21 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru