© 2021 Ольшевский Андрей Георгиевич репетитор по математике, информатике, программированию, физике по Скайп da.irk.ru

Сайт супер код ру super-code.ru наполняется наполняется полезными темами, которые можно скачать бесплатно

Векторы на плоскости и в пространстве, способы решения задач, примеры, формулы (продолжение)

Векторы на плоскости и в пространстве веб-страницы: 1 2 3

23 Косинус угла или угол между векторами

Косинус угла между двумя ненулевыми векторами = (x₁; y₁; z₁) и = (x₂; y₂; z₂) равен скалярному произведению векторов, деленному на произведение длин этих векторов

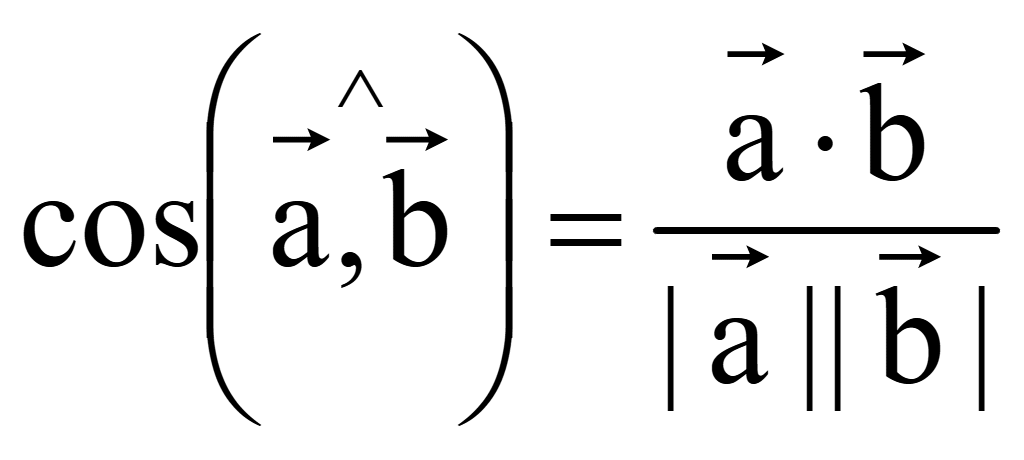
Косинус угла между векторами в координатах

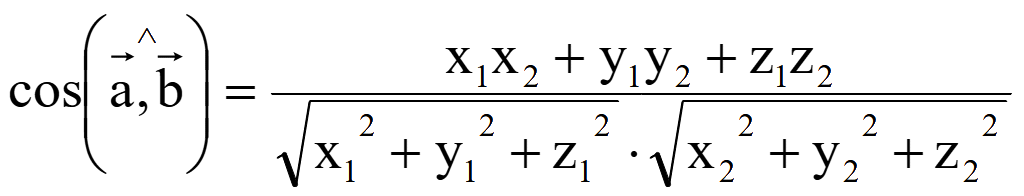
Угол между векторами

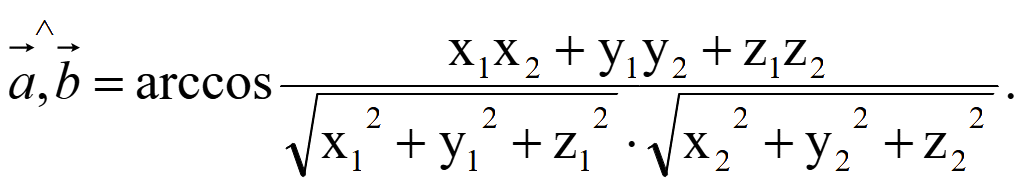
Если = 1, то угол между векторами равен 0⁰, векторы сонаправлены.

Если 0 < 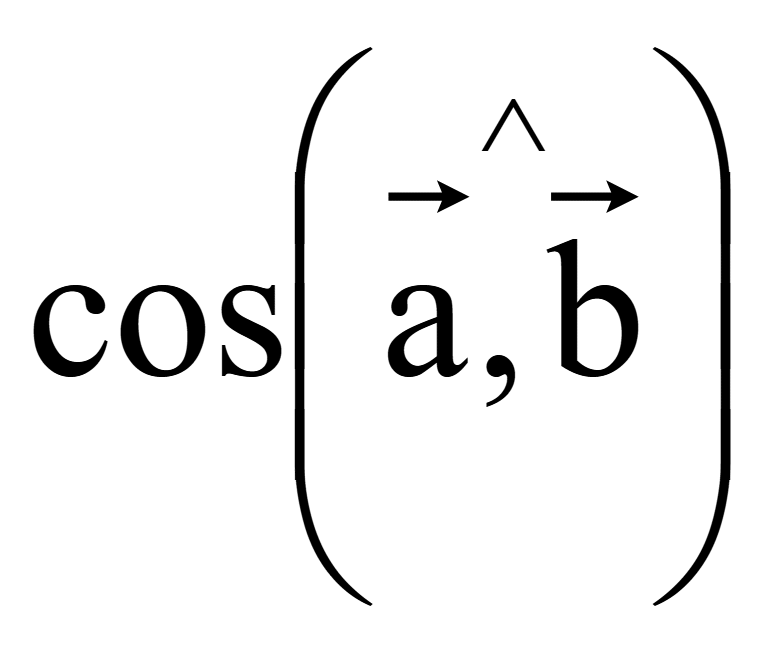< 1, то 0⁰ < < 90⁰.

Если 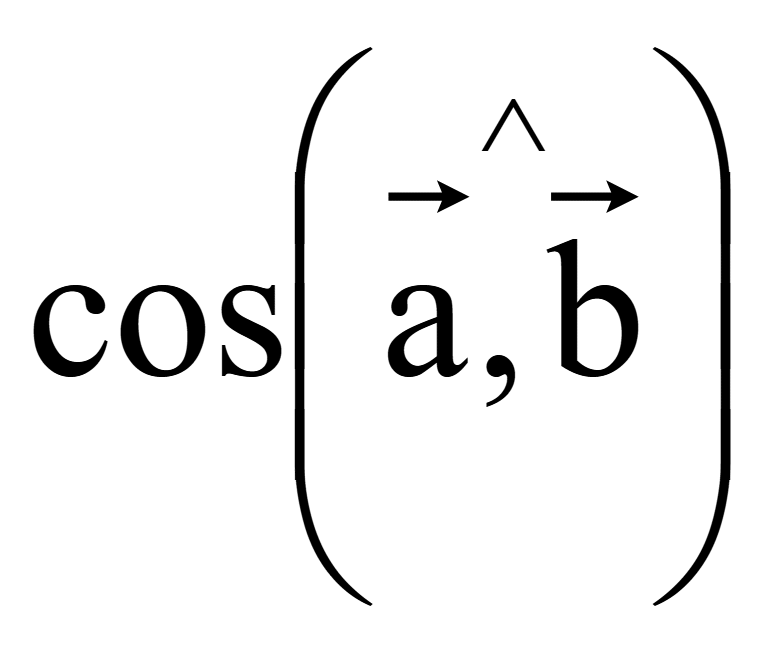= 0, то угол между векторами равен 90⁰, векторы перпендикулярны.

Если -1 < 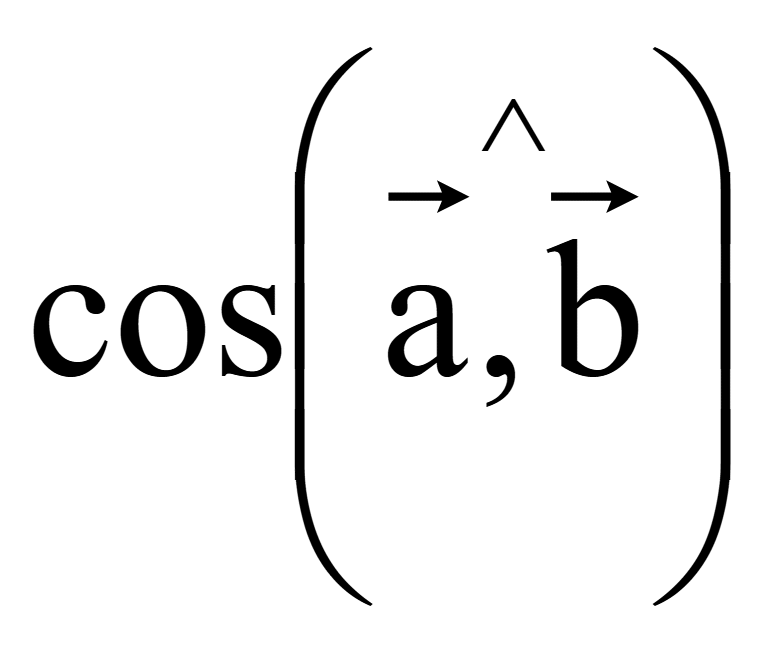< 0, то 90⁰ < < 180⁰.

Если 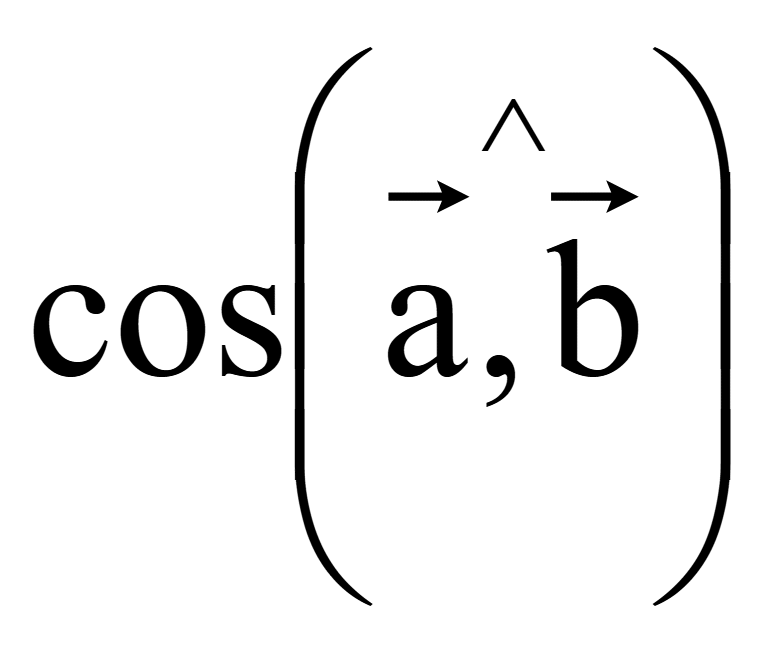= -1, то угол между векторами равен 180⁰, векторы противоположно направлены.

Повторимся. Если какой-то вектор задан координатами начала и конца, то отнимая от соответствующих координат конца вектора координаты начала, получаем координаты этого вектора.

Задача. Найти угол между векторами (0; -2; 0), (-2; 0; -4).

Решение

Скалярное произведение векторов

= 0·(-2) + (-2)·0 + 0·(-4) = 0,

следовательно угол между векторами равен = 90⁰.

24 Свойства скалярного произведения векторов

Свойства скалярного произведения справедливы при любых , , , k:

1. , если , то , если = , то = 0.

2. Переместительный закон

3. Распределительный закон

4. Сочетательный закон .

25 Направляющий вектор прямой

Направляющий вектор прямой - это ненулевой вектор, лежащий на заданной прямой или на прямой, параллельной данной прямой.

Если прямая M₁M₂ задана двумя точками M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂), то направляющим является вектор или противоположный ему вектор = - . Координаты направляющих векторов прямой M₁M₂

= (x₂ - x₁; y₂ - y₁; z₂ – z₁);

= (x₁ - x₂; y₁ - y₂; z₁ - z₂).

Систему координат желательно задать так, чтобы прямая проходила через начало координат, тогда координаты единственной точки на прямой, не совпадающей с началом координат и будут координатами направляющего вектора этой прямой.

Задача. Определить координаты направляющего вектора прямой, проходящей через точки M₁ (1; 0; 0), M₂ (0; 1; 0).

Решение

Построим заданные точки в системе координат Oxyz.

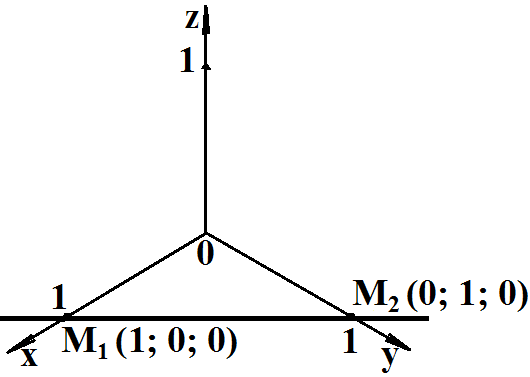
Направляющий вектор прямой проходящей через точки M₁(1; 0; 0), M₂ (0; 1; 0) обозначим . Каждая из его координат равна разности соответствующих координат конца и начала вектора

= (x₂ - x₁; y₂ - y₁; z₂ – z₁)

= (0 - 1; 1 - 0; 0 - 0) = (-1; 1; 0)

Изобразим направляющий вектор прямой в системе координат с началом в точке M₁, с концом в точке M₂ и равный ему вектор из начала координат с концом в точке M (-1; 1; 0)

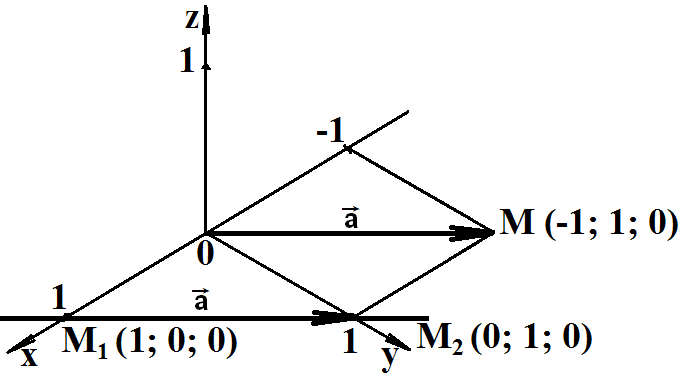
26 Угол между двумя прямыми

Возможные варианты взаимного расположения 2-х прямых на плоскости и угла между такими прямыми:

1. Прямые пересекаются в единственной точке, образуя 4 угла, 2 пары вертикальных углов попарно равны. Угол φ между двумя пересекающимися прямыми является углом, не превышающим три других угла между этими прямыми. Поэтому угол между прямыми 0⁰ < φ ≤ 90⁰.

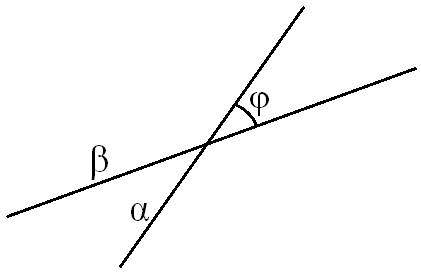
Пересекающиеся прямые могут быть, в частности, перпендикулярны φ = 90⁰.

2. Прямые параллельны, то есть не совпадают и не пересекаются, φ=0⁰.

3. Прямые совпадают, φ = 0⁰.

Угол между прямыми на плоскости может быть в диапазоне

0⁰ ≤ φ ≤ 90⁰.

Возможные варианты взаимного расположения 2-х прямых в пространстве и угла между такими прямыми:

1. Прямые пересекаются в единственной точке, образуя 4 угла, 2 пары вертикальных углов попарно равны. Угол φ между двумя пересекающимися прямыми является углом, не превышающим три других угла между этими прямыми. Поэтому угол между прямыми 0⁰ < φ ≤ 90⁰.

2. Прямые параллельны, то есть не совпадают и не пересекаются, φ=0⁰.

3. Прямые совпадают, φ = 0⁰.

4. Прямые скрещиваются, то есть не пересекаются в пространстве и не параллельны. Углом φ между скрещивающимися прямыми является угол между прямыми, проведенными параллельно этим прямым так, чтобы они пересекались. Поэтому угол между скрещивающимися прямыми

0⁰ < φ ≤ 90⁰.

Угол между 2-мя прямыми в пространстве равен углу между прямыми, проведенными параллельно этим прямым в одной плоскости. Поэтому угол между прямыми в пространстве может быть в диапазоне

0⁰ ≤ φ ≤ 90⁰.

26.1 Косинус угла между направляющими векторами прямых

Угол θ (тета) между векторами и может быть в диапазоне

0⁰ ≤ θ ≤ 180⁰.

Если угол φ между прямыми α и β равен углу θ между направляющими векторами этих прямых φ = θ, то равны и косинусы этих углов

cos φ = cos θ.

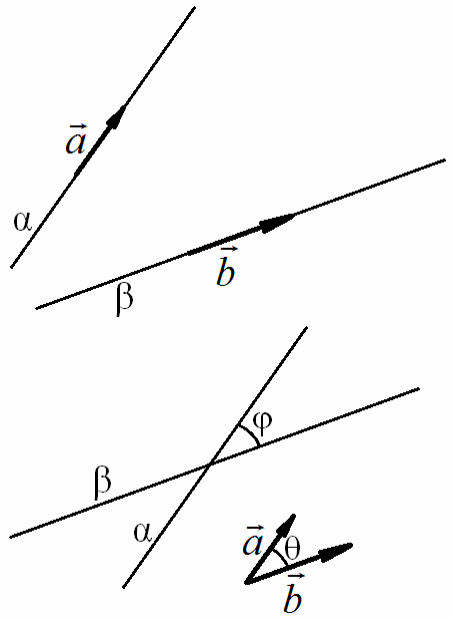
Если угол между направляющими векторами прямых θ > 90⁰, то угол между прямыми φ = 180⁰ - θ и

cos φ = cos (180⁰ - θ) = - cos θ.

cos φ = - cos θ.

Этот случай изображен на рисунке

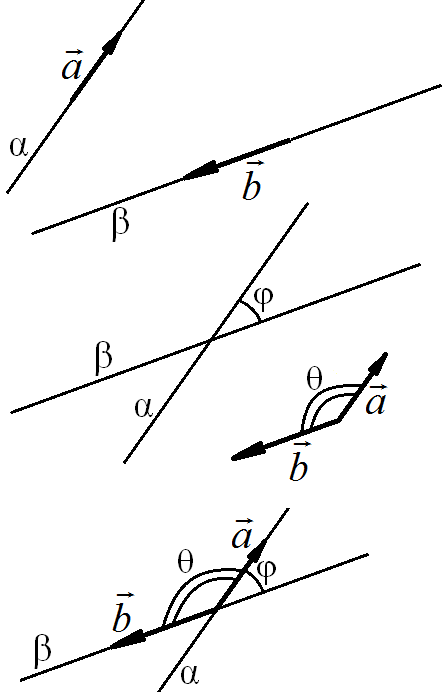
Поэтому косинус угла между прямыми всегда равен модулю косинуса угла между векторами

cos φ = |cos θ|.

Если заданы координаты ненулевых векторов = (x₁; y₁; z₁) и = (x₂; y₂; z₂), то косинус угла θ между ними

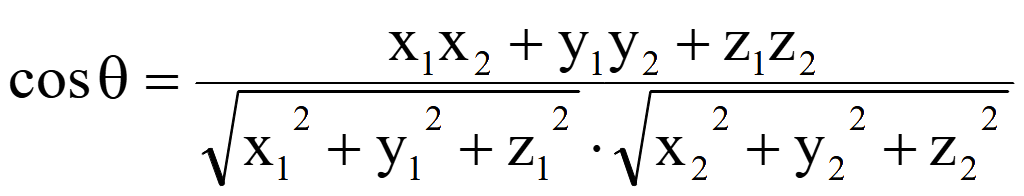
Косинус угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых

cos φ = |cos θ| =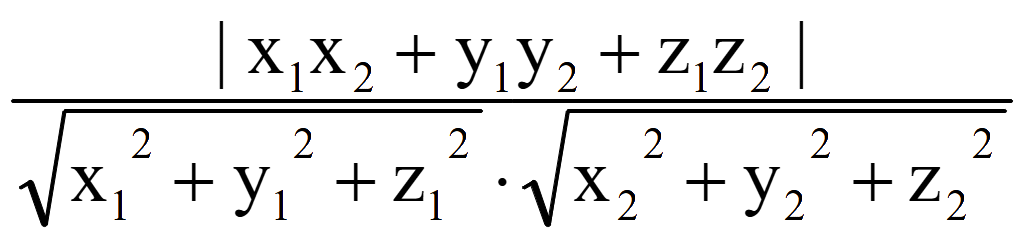

Для лучшего запоминания сформулируем следующее правило. Прямые являются одинаковыми геометрическими объектами, поэтому и одинаковые тригонометрические функции cos присутствуют в формуле.

Косинус угла между прямыми

cos φ =

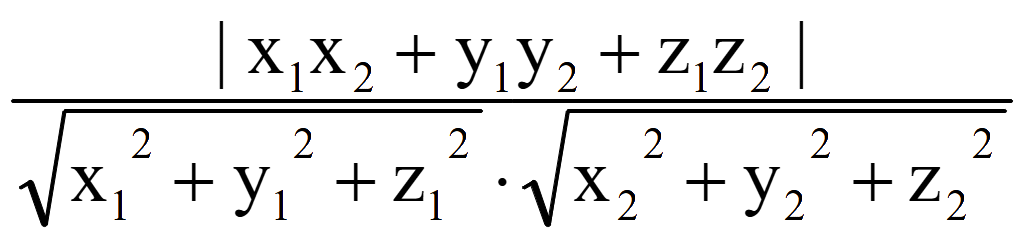
Угол между прямыми

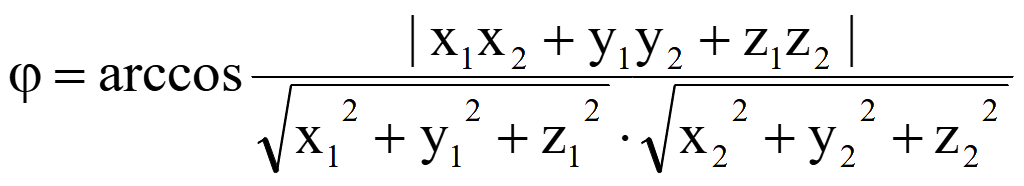
Если каждая из двух прямых задана двумя точками, то можно определить направляющие векторы этих прямых и косинус угла между прямыми.

Если cos φ = 1, то угол φ между прямыми равен 0⁰, можно принять для этих прямых один из направляющих векторов этих прямых, прямые параллельны или совпадают. Если прямые не совпадают, то они параллельны. Если прямые совпадают, то любая точка одной прямой принадлежит другой прямой.

Если скалярное произведение направляющих ненулевых векторов прямых = (x₁; y₁; z₁) и = (x₂; y₂; z₂) равно нулю

x₁x₂ + y₁y₂ + z₁z₂ = 0

и, следовательно, cos φ = 0, то угол φ между прямыми 90⁰ (прямые перпендикулярны), прямые пересекаются или скрещиваются. Если прямые не пересекаются, то они скрещиваются. Если прямые пересекаются, то они имеют общую точку.

Если 0 ≤ cos φ < 1, то угол между прямыми 0⁰ < φ ≤ 90⁰, прямые пересекаются или скрещиваются. Если прямые не пересекаются, то они скрещиваются. Если прямые пересекаются, то они имеют общую точку.

Задача. Определить угол между прямыми M₁M₃ и M₂M₃ с координатами точек M₁ (1; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1).

Решение

Построим заданные точки и прямые в системе координат Oxyz.

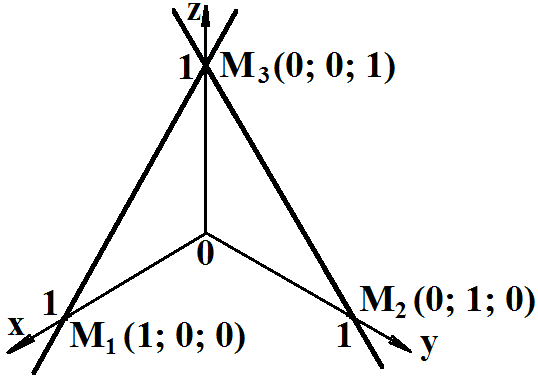
Направляющие векторы прямых направим так, чтобы угол θ между векторами был меньше 90⁰

θ > 90⁰,

тогда он будет совпадать с углом φ между заданными прямыми. Изобразим векторы = и = , а также углы θ и φ:

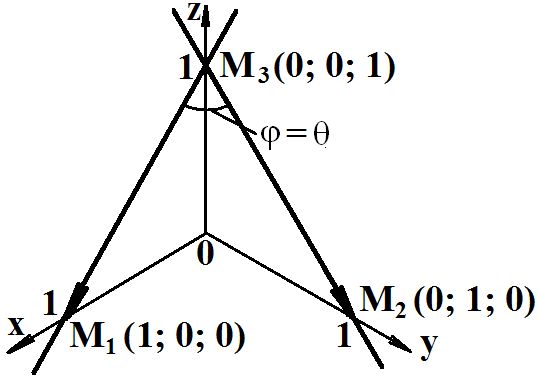
Определим координаты направляющих векторов и

= = (1 - 0; 0 - 0; 0 - 1) = (1; 0; -1);

= = (0 - 0; 1 - 0; 0 - 1) = (0; 1; -1).

Косинус угла между прямыми равен косинусу угла между векторами

cos φ = cos θ =

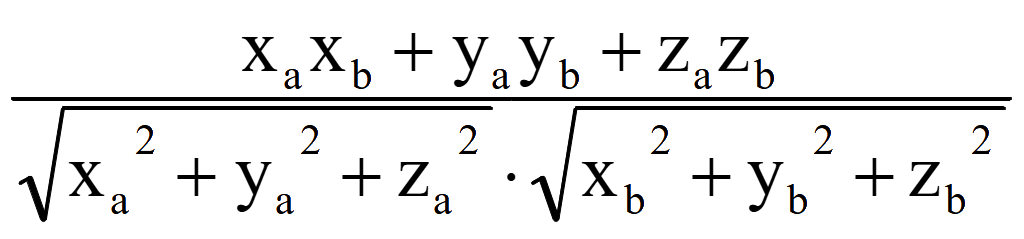
cos φ = cos θ =

Следовательно, углы равны

φ = θ = 60⁰.

Ответ: угол между прямыми φ = 60⁰.

27 Нормальный вектор прямой

Нормальный вектор прямой - это вектор перпендикулярный прямой.

28 Нормальный вектор плоскости

Нормальный вектор плоскости - это вектор перпендикулярный плоскости.

29 Общее уравнение плоскости

Общее (нормальное) уравнение плоскости

ax + by + cz + d = 0,

где a, b, c - координаты нормального (перпендикулярного к плоскости) ненулевого вектора плоскости (a; b; c) (вектор ненулевой, поэтому его координаты одновременно не равны нулю и его длина в квадрате не равна нулю | |² = a² + b² + c² ≠ 0).

Особые положения плоскости:

- плоскость проходит через начало координат при d = 0 и уравнение плоскости имеет вид ax + by + cz = 0, поэтому желательно задавать систему координат так, чтобы плоскость проходила через начало координат для упрощения уравнения плоскости;

- плоскость параллельна той оси координат, обозначение которой отсутствует в уравнении плоскости и, следовательно, соответствующий коэффициент равен нулю, например, при c = 0 плоскость параллельна оси Oz и не содержит z в уравнении ax + by + d = 0. В этом случае на положение плоскости не влияет координата z;

- плоскость содержит ту ось координат, обозначение которой отсутствует, следовательно, соответствующий коэффициент равен нулю и d = 0, например, при c = d = 0 плоскость содержит ось Oz, но не содержит z и d в уравнении ax + by = 0;

- плоскость параллельна координатной плоскости, обозначения которой отсутствуют в уравнении плоскости и, следовательно, соответствующие коэффициенты равны нулю, например, при b = c = 0 плоскость параллельна координатной плоскости Oyz и не содержит y, z в уравнении ax + d = 0.

- если плоскость совпадает с координатной плоскостью, то уравнение такой плоскости представляет из себя равенство нулю обозначения координатной оси, перпендикулярной данной координатной плоскости, например, при x = 0 заданная плоскость является координатной плоскостью Oyz.

Желательно задавать систему координат так, чтобы плоскость была параллельна или совпадала с как можно большим числом осей координат для значительного упрощения уравнения плоскости.

Задача. Нормальный вектор задан уравнением

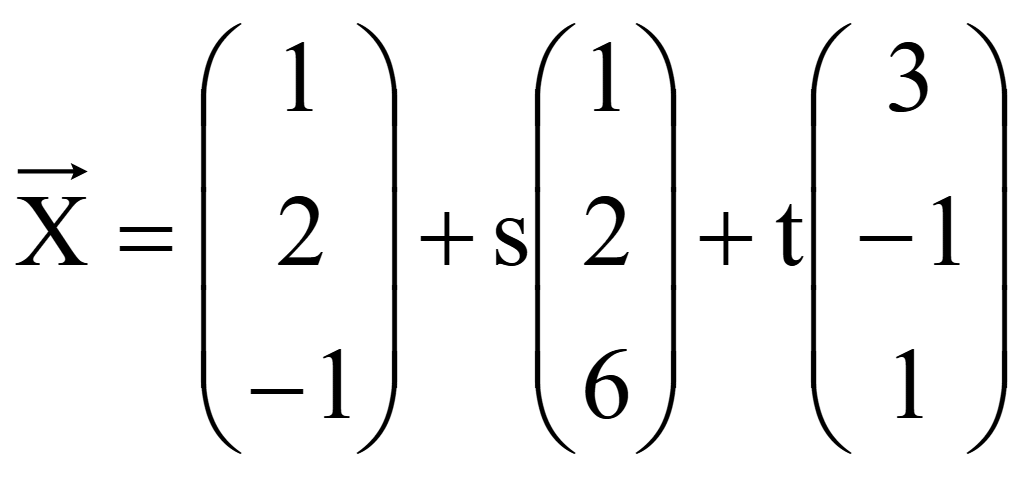
Представить уравнение плоскости в нормальной форме.

Решение

Координаты нормального вектора

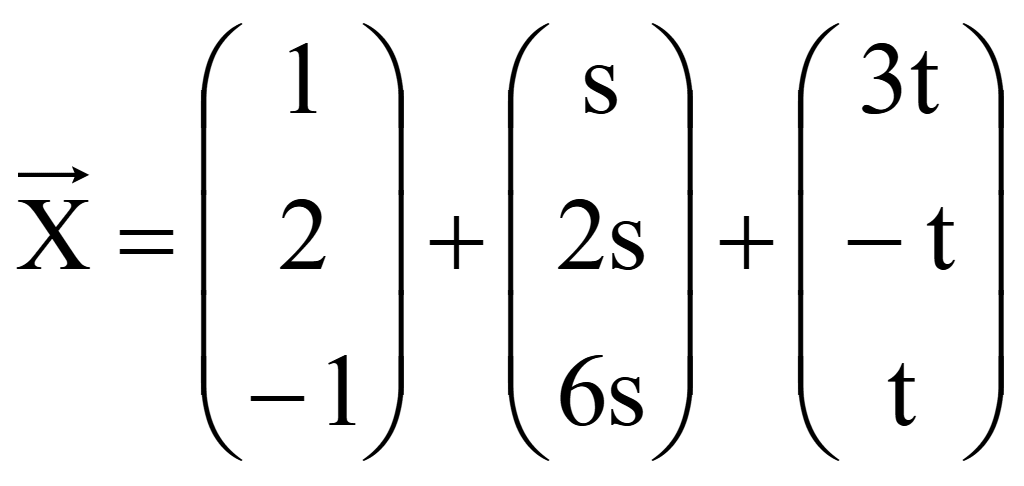
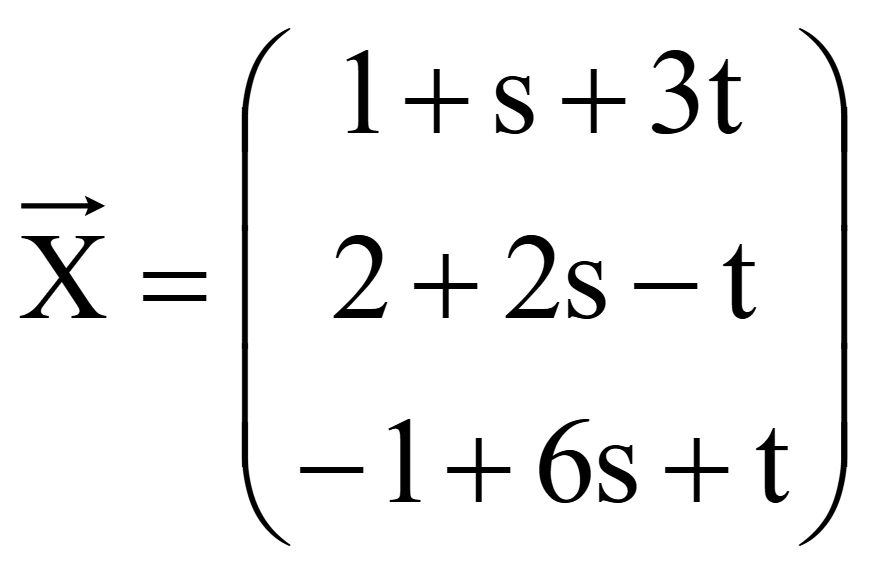
= (a; b; c) = (1+s+3t; 2+2s-t; -1+6s+t)

Уравнение плоскости в нормальной форме, проходящей через начало координат

(1+s+3t)x + (2+2s-t)y + (-1+6s+t)z = 0.

30 Уравнение плоскости, проходящей через точку перпендикулярно вектору

Если дана точка M₀ (x₀; y₀; z₀), через которую проходит плоскость перпендикулярно не нулевому вектору (a; b; c), то можно подставить координаты точки M₀ (x₀; y₀; z₀) и координаты a, b, c нормального вектора в общее уравнение плоскости

ax + by + cz + d = 0 (1)

Получаем уравнение с одной неизвестной d

ax₀ + by₀ + cz₀ + d = 0

Отсюда

d = -(ax₀ + by₀ + cz₀)

Уравнение плоскости (1) после подстановки d

ax + by + cz - (ax₀ + by₀ + cz₀) = 0

раскроем скобки

ax + by + cz - ax₀ - by₀ - cz₀ = 0

сгруппирует относительно коэффициентов a, b и c

ax - ax₀ + by - by₀ + cz - cz₀ = 0

Вынесем за скобки коэффициенты a, b и c. Получаем уравнение плоскости, проходящей через точку M₀ (x₀; y₀; z₀) перпендикулярно не нулевому вектору (a; b; c)

a(x - x₀) + b(y - y₀) + c(z - z₀) = 0

Это уравнение можно получить, если для заданной точки M₀ (x₀; y₀; z₀) выбрать произвольную точку M (x; y; z) на плоскости и найти скалярное произведение вектора = (x - x₀; y - y₀; z – z₀) с перпендикулярным к плоскости вектором (a; b; c), которое должно быть равно нулю

a(x - x₀) + b(y - y₀) + c(z - z₀) = 0.

Если теперь раскроем скобки

ax - ax₀ + by - by₀ + cz - cz₀ = 0

ax + by + cz - ax₀ - by₀ - cz₀ = 0

Обозначим

d = - ax₀ - by₀ - cz₀

То получим общее уравнение плоскости

ax + by + cz + d = 0.

31 Уравнение плоскости, перпендикулярной прямой, заданной двумя точками

Заданные точки M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂) образуют нормальный вектор искомой плоскости, определим координаты вектора . Каждая из его координат равна разности соответствующих координат конца и начала вектора

= (x₂ - x₁; y₂ - y₁; z₂ – z₁) = (a, b, c)

Подставляем координаты нормального вектора в общее уравнение плоскости

ax + by + cz + d = 0

и получаем уравнение искомой плоскости, в котором d может быть любым

(x₂ - x₁)x + (y₂ – y₁)y + (z₂ – z₁)z + d = 0.

Плоскостей, перпендикулярных заданному вектору может быть бесконечное множество. Если задать координаты какой-то точки на этой плоскости и подставить эти координаты вместо x, y, z в найденное уравнение плоскости выше, то можно будет определить d

d = -((x₂ - x₁)x + (y₂ – y₁)y + (z₂ – z₁)z)

и единственное уравнение этой плоскости.

32 Уравнение плоскости, проходящей через середину отрезка перпендикулярно этому отрезку

Если заданы точки M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂), то уравнение плоскости, перпендикулярной вектору

(x₁ - x₂)x + (y₁ – y₂)y + (z₁ – z₂)z + d = 0.

Эта плоскость проходит через середину отрезка, образованного заданными точками. Координаты середины отрезка M₁M₂

, ,

Подставим координаты x, y, z

Отсюда

Подставим и получим уравнение плоскости, лежащей на одинаковом расстоянии от двух точек

(x₁ - x₂)x + (y₁ - y₂)y + (z₁ - z₂)z =0

Можно за нормальный принять и другое направление вектора

= (x₂ - x₁; y₂ - y₁; z₂ – z₁) = (a, b, c);

ax + by + cz + d = 0.

33 Определение координаты точки, лежащей на плоскости, расположенной на одинаковом расстоянии от двух точек

Точка, лежащая на одинаковом кратчайшем расстоянии от двух точек M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂) располагается в центре отрезка M₁M₂, поэтому координаты такой точки О равны половинам соответствующих координат концов отрезка

Искомая произвольная точка в любом случае лежит в плоскости, перпендикулярной вектору, образованному заданными точками и проходит через середину вектора .

Уравнение этой плоскости определили выше

(x₁ - x₂)x + (y₁ - y₂)y + (z₁ - z₂)z =0.

Нормальный вектор этой плоскости

= (a, b, c);

Получили уравнение плоскости, лежащей на одинаковом расстоянии от двух точек

ax + by + cz + d = 0

Если искомая точка лежит на оси x, то y = 0 и z = 0 и уравнение плоскости значительно упрощается

ax + d = 0

Отсюда координата x

Координаты искомой точки

O (x; 0; 0);

Если искомая точка лежит на оси y, то x = 0 и z = 0 и уравнение плоскости также значительно упрощается

by + d = 0

Отсюда координата y

Координаты точки О(0; y; 0).

Если искомая точка лежит на оси z, то x = 0 и y = 0 и уравнение плоскости также значительно упрощается

cz + d = 0

Отсюда координата z

Координаты точки О(0; 0; z).

Систему координат желательно задавать так, чтобы искомая точка лежала на одной из осей координат.

34 Уравнение плоскости, проходящей через две точки и начало координат

Определим коэффициенты общего уравнения плоскости

ax + by + cz + d = 0.

Систему координат желательно задать так, чтобы плоскость проходила через начало этой системы координат. Точки M₁ (x₁; y₁; z₁) и M₂ (x₂; y₂; z₂), лежащие в этой плоскости, необходимо задать так, чтобы прямая, соединяющая эти точки не проходила через начало координат.

Плоскость будет проходить через начало координат, поэтому d = 0. Тогда общее уравнение плоскости принимает вид

ax + by + cz = 0.

Неизвестно 3 коэффициента a, b, c. Подстановка координат двух точек M₁ (x₁; y₁; z₁) и M₂ (x₂; y₂; z₂) в общее уравнение плоскости дает систему 2-х уравнений:

Система 2-уравнений позволяет определить лишь 2-е неизвестные величины. Требуются особые приемы для решения данной системы уравнений.

Если принять какой-то коэффициент в общем уравнении плоскости равным единице, например, a = 1, тогда полученная система 2-х уравнений

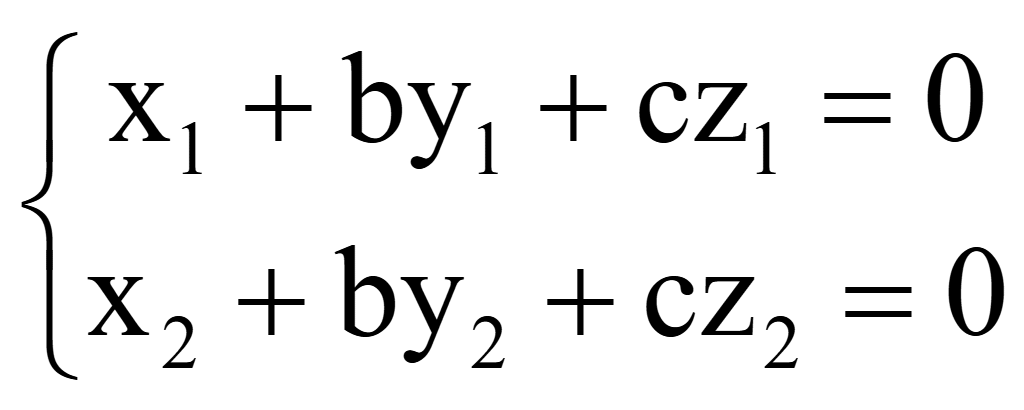
позволит определить оставшиеся 2 неизвестные коэффициенты b и c.

Если одна из координат точки нулевая, то за единицу принимается коэффициент, соответствующий этой координате. Если у какой-то точки две координаты нулевые, то за единицу принимается коэффициент, соответствующий одной из этих нулевых координат.

Если принимается a = 1, тогда система 2-х уравнений позволит определить 2 неизвестных коэффициента b и c:

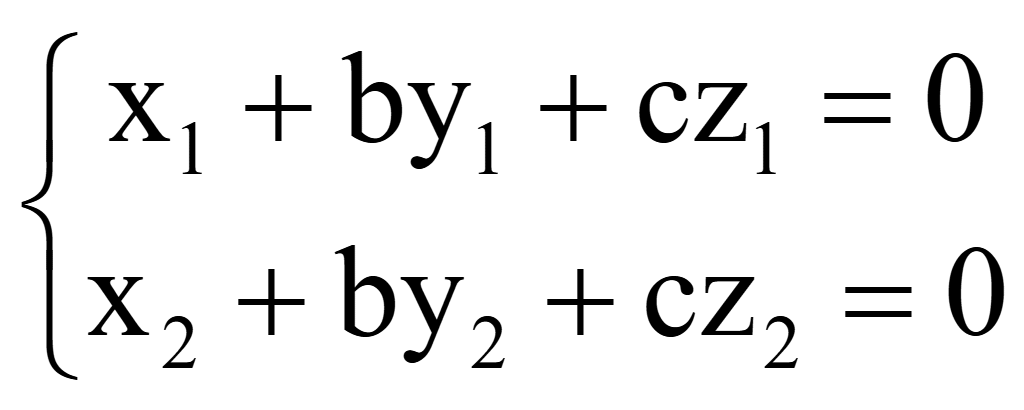
Коэффициенты, являющиеся заданными координатами точек, ставятся впереди неизвестных b и c, а свободные от неизвестных члены, содержащие лишь заданные координаты, переносятся в правую часть уравнений

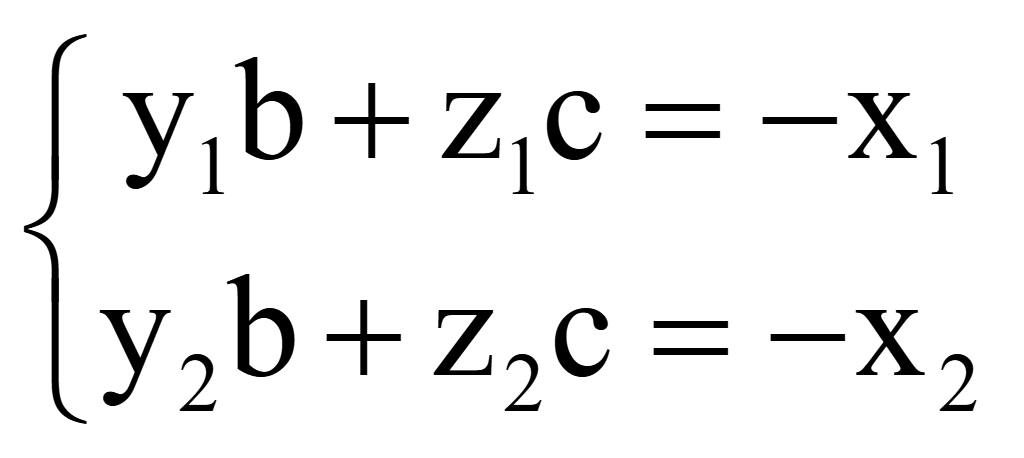
Систему этих уравнений проще решить методом исключений (метод Гаусса в высшей школе), помножив какое-то уравнение на такое число, чтобы коэффициенты при какой-то неизвестной стали равны. Тогда разность уравнений позволит исключить эту неизвестную и определить другую неизвестную. Подстановка найденной неизвестной в любое уравнение позволит определить и вторую неизвестную.

35 Уравнение плоскости, проходящей через три точки

Определим коэффициенты общего уравнения плоскости

ax + by + cz + d = 0,

проходящей через точки M₁ (x₁; y₁; z₁), M₂ (x₂; y₂; z₂) и M₃ (x₃; y₃; z₃). У точек не должно быть двух одинаковых координат.

Неизвестно 4 коэффициента a, b, c и d. Подстановка координат трех точек в общее уравнение плоскости дает систему 3-х уравнений. Принять какой-то коэффициент в общем уравнении плоскости равным единице, тогда система 3-х уравнений позволит определить 3 неизвестных коэффициента. Обычно принимается a = 1, тогда система 3-х уравнений позволит определить 3 неизвестных коэффициента b, c и d:

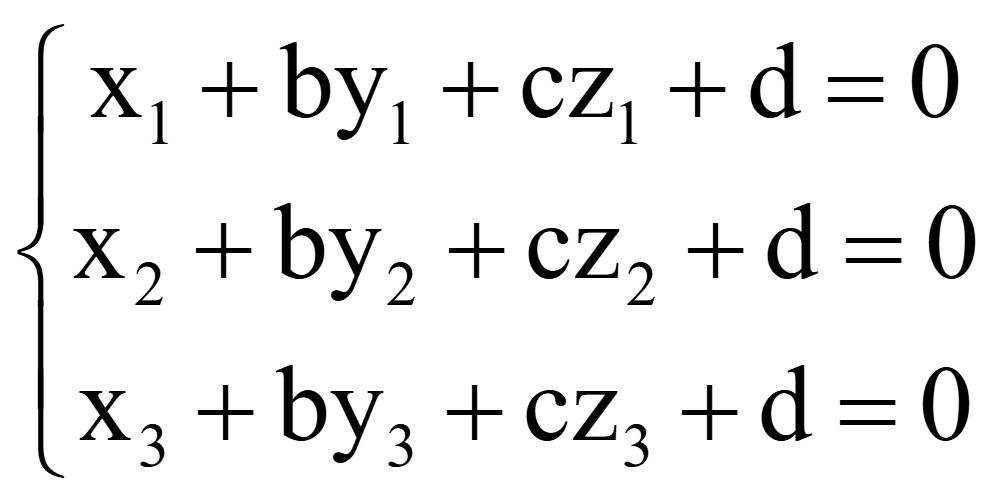
Систему уравнений лучше решать методом исключения неизвестных (методом Гаусса). Можно переставлять уравнения в системе. Любое уравнение можно умножить или поделить на любой коэффициент не равный нулю. Любые два уравнения можно сложить и результирующее уравнение записать вместо любого из этих двух складываемых уравнений. Из уравнений исключаются неизвестные, получением нулевого коэффициента перед ними. В одном уравнении, обычно самом нижнем оставляется одна переменная, которая легко определяется. Найденная переменная подставляется во второе уравнение снизу, в котором обычно оставляется 2 неизвестные. Уравнения решаются снизу вверх и определяются все неизвестные коэффициенты.

Коэффициенты ставятся впереди неизвестных, а свободные от неизвестных члены переносятся в правую часть уравнений

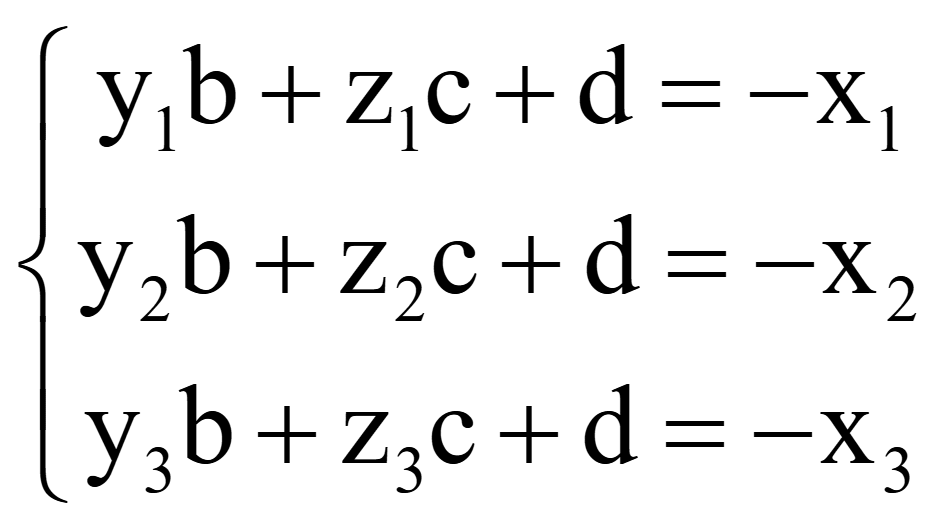
В верхнюю строку обычно ставится уравнение, имеющее коэффициент 1 перед первой или любой неизвестной, или все первое уравнение делится на коэффициент перед первой неизвестной. В данной системе уравнений разделим первое уравнение на y₁

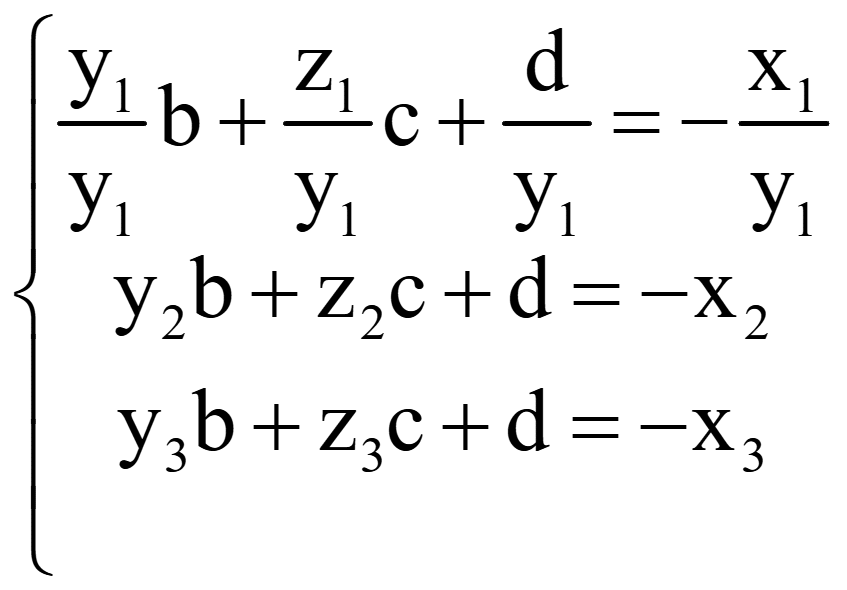
Перед первой неизвестной получили коэффициент 1:

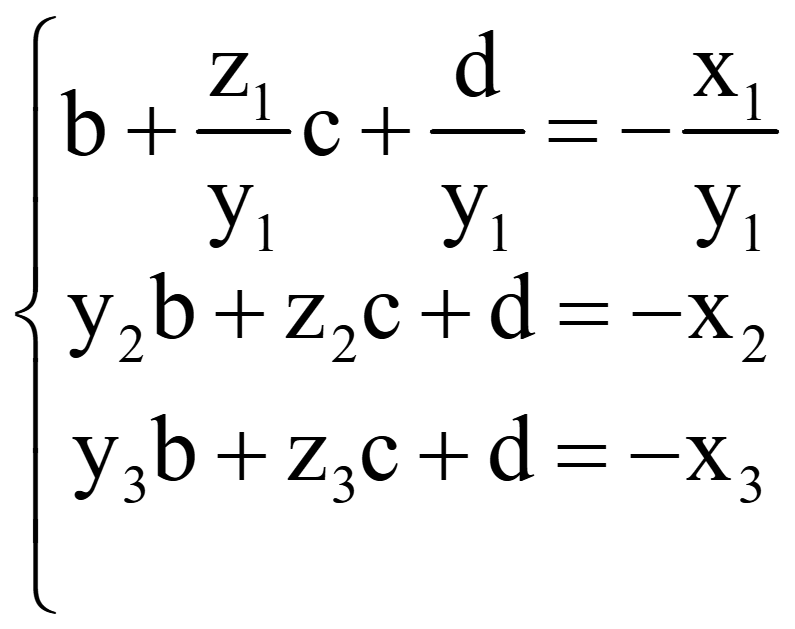
Для обнуления коэффициента перед первой переменной второго уравнения помножим первое уравнение на -y₂, сложим его со вторым уравнением и полученное уравнение запишем вместо второго уравнения. Первая неизвестная во втором уравнении будет исключена, потому что

y₂b - y₂b = 0.

Аналогично исключаем первую неизвестную в третьем уравнении, помножив первое уравнение на -y₃, сложив его с третьим уравнением и полученное уравнение записав вместо третьего уравнения. Первая неизвестная в третьем уравнении будет также исключена, потому что

y₃b - y₃b = 0.

Аналогично исключаем вторую неизвестную в третьем уравнении. Решаем систему снизу вверх.

Задача. Определить общее уравнение плоскости

ax + by + cz + d = 0,

проходящей через точки M₁ (0; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1).

Решение

Построим заданные точки в системе координат xyz.

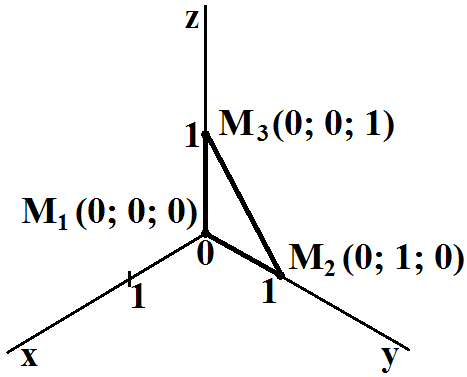
Примем a = 1. Подстановка координат трех точек в общее уравнение плоскости дает систему 3-х уравнений

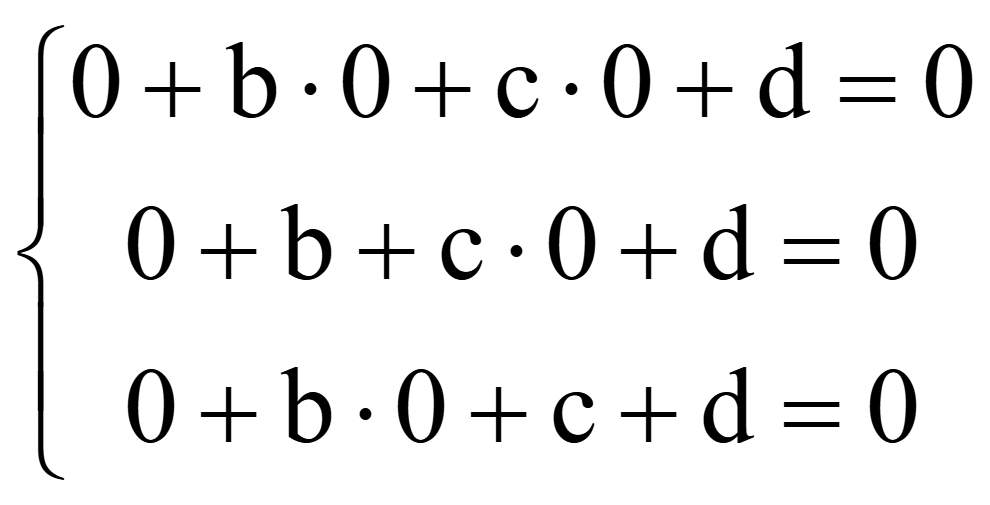
Координаты нормального ненулевого вектора плоскости (1; 0; 0), изобразим его в системе координат

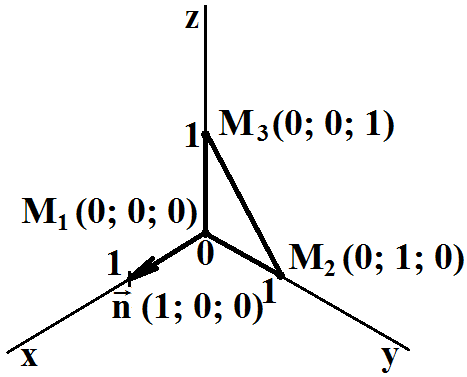
Общее уравнение плоскости

x + 0·y + 0·z + 0 = 0

x = 0.

Заданная плоскость является координатной плоскостью Oyz.

Задача. Определить общее уравнение плоскости

ax + by + cz + d = 0,

проходящей через точки M₁ (1; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1).

Решение

Построим заданные точки M₁ (1; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1) в системе координат Oxyz.

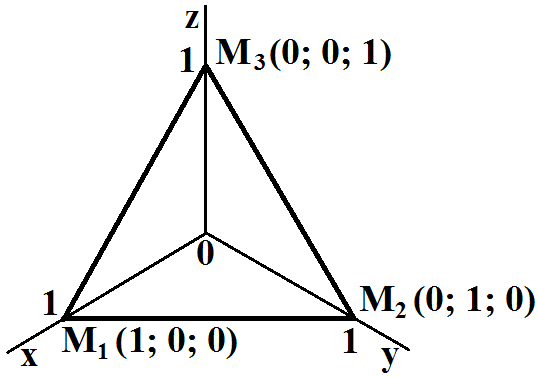
Примем a = 1. Подстановка координат трех точек в общее уравнение плоскости дает систему 3-х уравнений

; ;

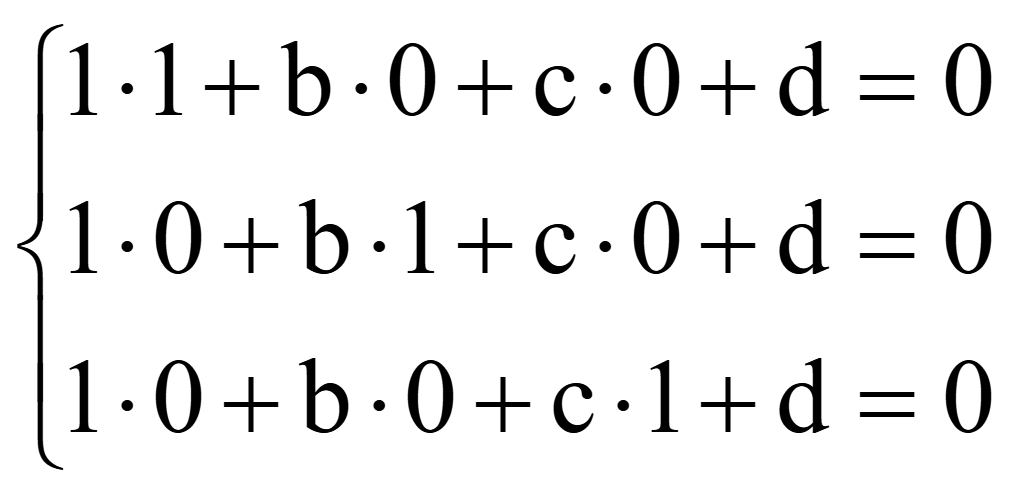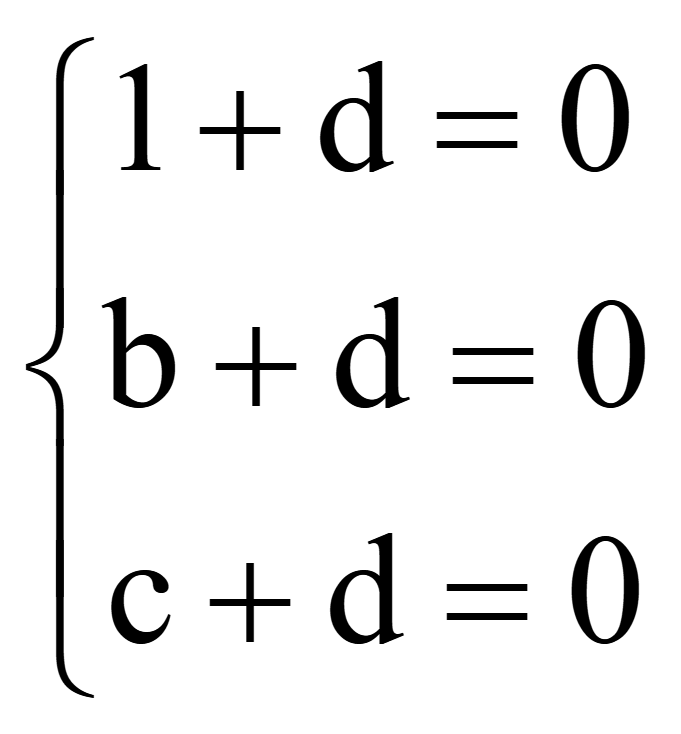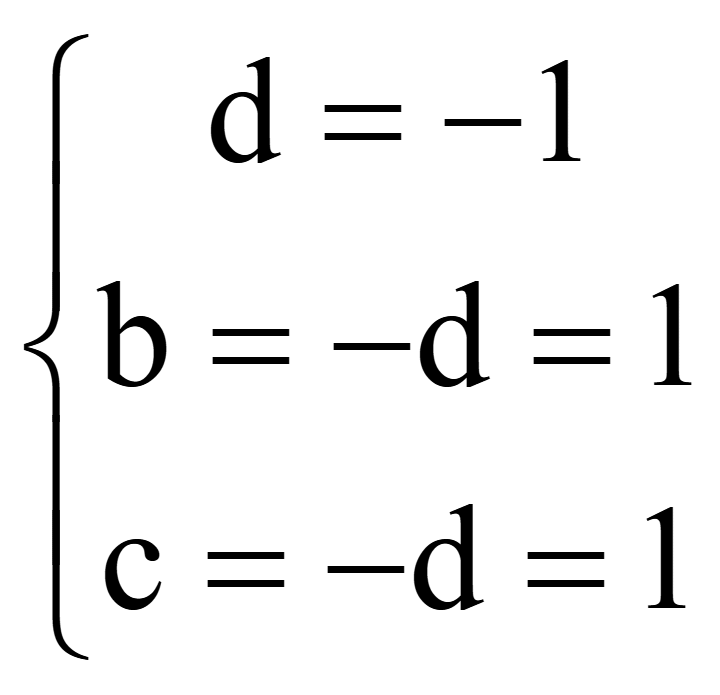
Координаты нормального ненулевого вектора плоскости (1; 1; 1), в изображенной ранее системе координат он будет изображен точкой, поэтому покажем проекции нормального вектора на плоскости xOy, yOz, xOz.

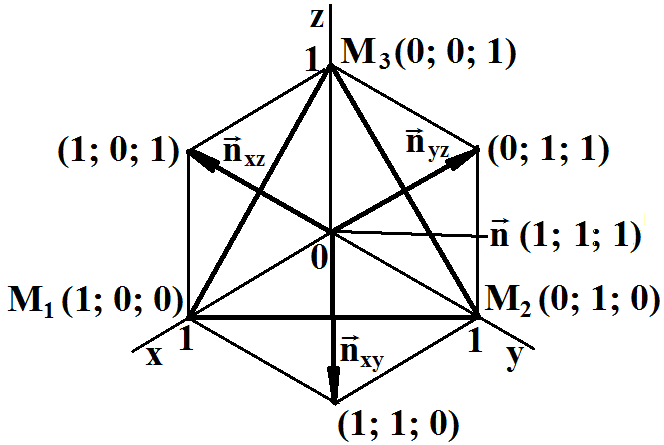
Общее уравнение плоскости

x + y + z - 1 = 0.

36 Угол между прямой и плоскостью

Угол φ (см. рисунок) между прямой α и плоскостью β равен углу между направляющим вектором прямой и проекцией α' прямой α на плоскость β. Проекция прямой α' на плоскость β лежит в плоскости β, поэтому перпендикулярна вектору , нормальному к плоскости β.

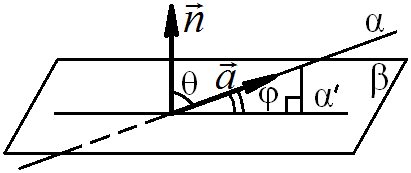
Угол θ (тэта) между направляющим вектором прямой и нормальным вектором плоскости:

θ = 90⁰ - φ.

Отсюда угол между прямой и плоскостью

φ = 90⁰ - θ

sin φ = sin (90⁰ - θ),

но по формуле приведения

sin (90⁰ - θ) = cos θ.

Получаем

sin φ = cos θ.

Если угол между векторами θ = 90⁰ + φ (см. рисунок ниже), тогда угол между прямой и плоскостью равен

φ = θ - 90⁰ = -(90⁰ - θ).

sin φ = sin (-(90⁰ - θ)) = -sin(90⁰ - θ) = -cos θ.

sin φ = - cos θ.

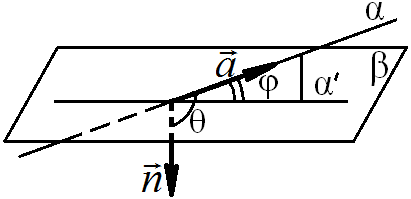
φ ≤ 90⁰, а 0 ≤ θ ≤ 180⁰, поэтому синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором плоскости

sin φ = |cos θ|

Если заданы координаты ненулевых векторов = (x₁; y₁; z₁) и = (x₂; y₂; z₂), то косинус угла θ между ними

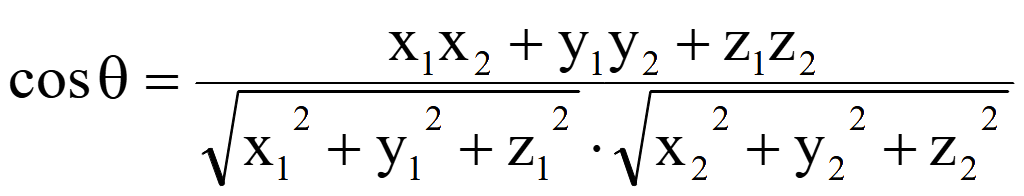
Синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой = (x₁; y₁; z₁) и нормальным вектором = (x₂; y₂; z₂) плоскости x₂x + y₂y + z₂z + d = 0

sin φ = |cos θ| =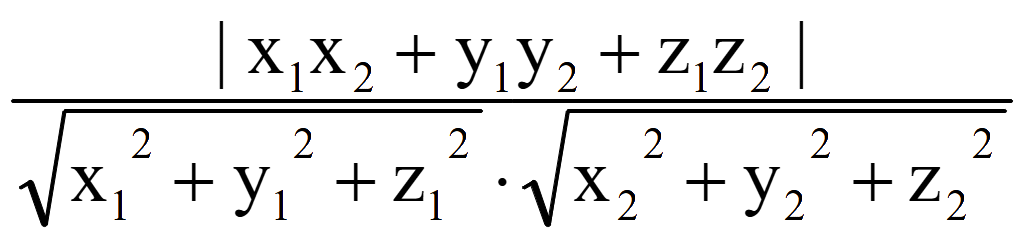

Для лучшего запоминания сформулируем следующее правило. Прямая и плоскость - это разные геометрические объекты, поэтому в формуле присутствуют и разные тригонометрические функции.

Синус угла между прямой и плоскостью

sin φ =

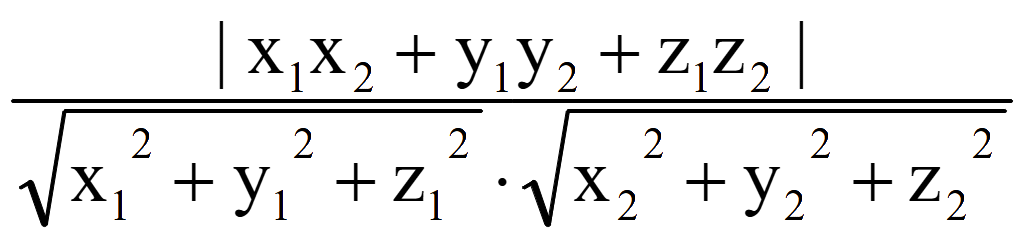
Угол между прямой и плоскостью

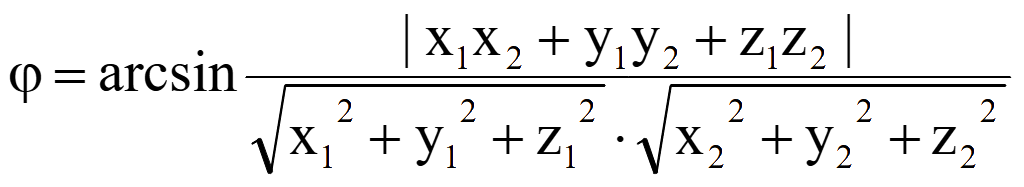
Если sin φ = 1, то угол φ между прямой и плоскостью равен 90⁰, Прямая и плоскость пересекаются в одной точке.

Если скалярное произведение направляющего ненулевого вектора прямой = (x₁; y₁; z₁) и ненулевого нормального вектора плоскости = (x₂; y₂; z₂) равно нулю

x₁x₂ + y₁y₂ + z₁z₂ = 0

и, следовательно, sin φ = 0, то угол φ между прямой и плоскостью равен 0⁰, прямая и плоскость параллельны или прямая лежит в плоскости. Если прямая и плоскость имеют одну общую точку, то прямая лежит в плоскости.

Если 0 < sin φ ≤ 1, то угол между прямой и плоскостью 0⁰ < φ ≤ 90⁰, прямая и плоскость пересекаются в одной точке.

Задача. Определить угол между плоскостью, проходящей через точки M₁ (0; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1), и прямой, проходящей через точки M₄ (1; 0; 0), M₂ (0; 1; 0).

Решение

Построим заданные точки, плоскость в виде треугольника, лежащего в ней, прямую в системе координат Oxyz.

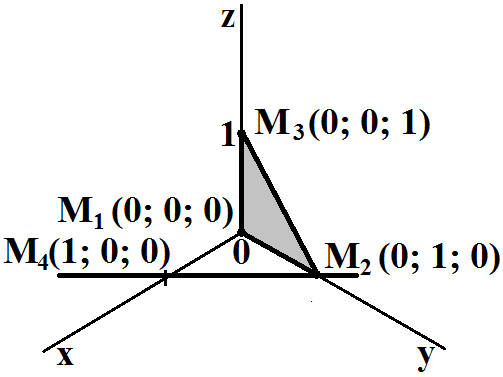
Координаты x всех точек плоскости равны 0, поэтому примем a=1. Подстановка координат трех точек в общее уравнение плоскости

ax + by + cz + d = 0

дает систему 3-х уравнений, позволяющую найти 3 неизвестных коэффициента b, c, d

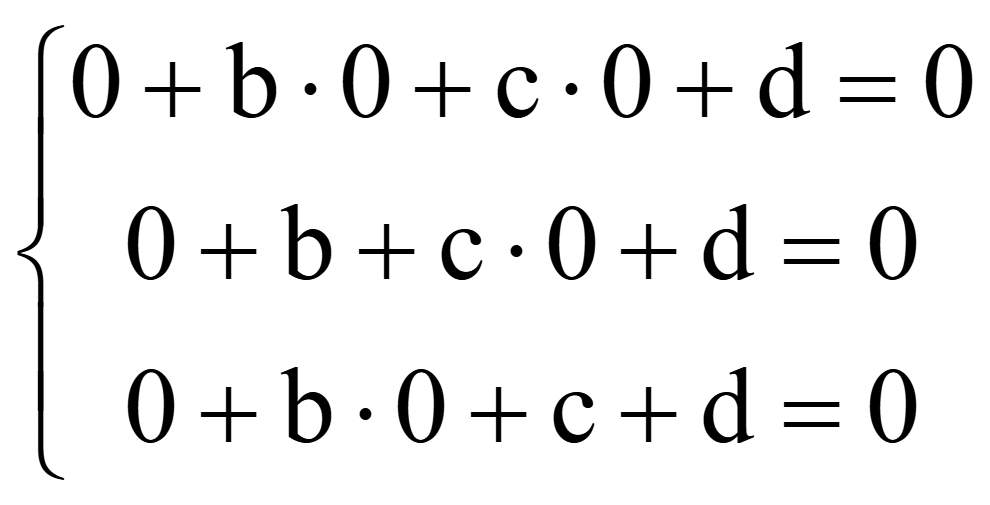
Координаты нормального ненулевого вектора плоскости (1; 0; 0), изобразим его в системе координат

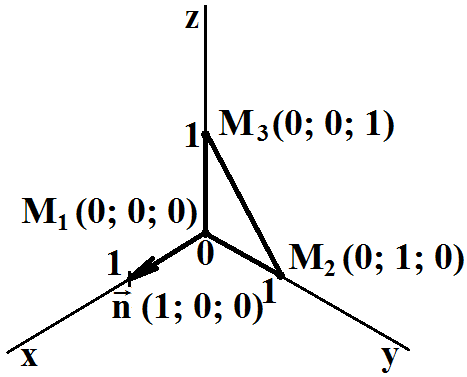
Общее уравнение плоскости

x + 0·y + 0·z + 0 = 0

x = 0.

Заданная плоскость является координатной плоскостью Oyz.

Направляющий вектор прямой проходящей через точки M₄(1; 0; 0), M₂ (0; 1; 0) обозначим . Каждая из его координат равна разности соответствующих координат конца и начала вектора

= (x₂ - x₄; y₂ - y₄; z₂ – z₄)

= (0 - 1; 1 - 0; 0 - 0) = (-1; 1; 0)

Изобразим направляющий вектор прямой в системе координат с началом в точке M₄, с концом в точке M₂ и равный ему вектор из начала координат с концом в точке M (-1; 1; 0)

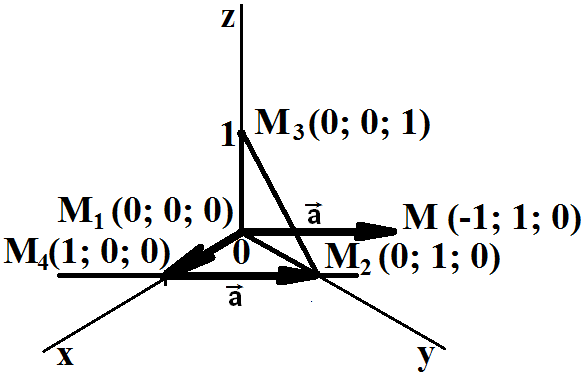
Если ненулевые векторы и , то косинус угла θ между ними

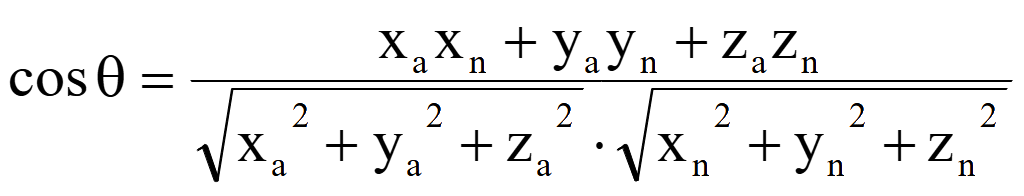
Синус угла между прямой и плоскостью

sin φ = |cos θ| =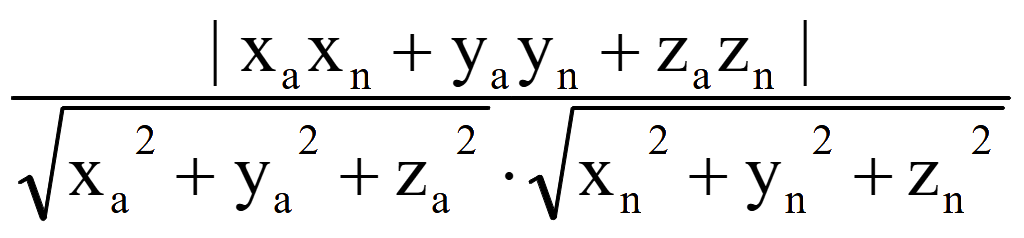

Подставляем координаты направляющего вектора прямой = {-1; 1; 0} и координаты нормального вектора плоскости = {1; 0; 0}.

sin φ =

sin φ =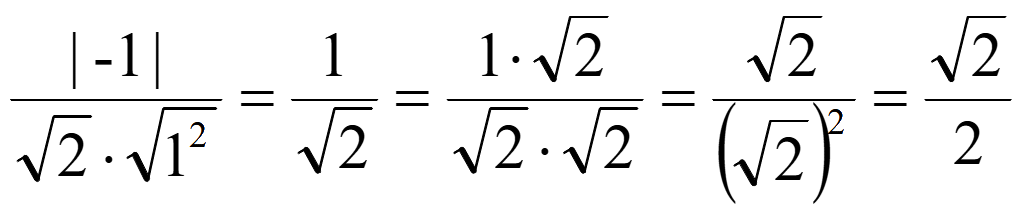

φ = 45⁰.

Изобразим угол между прямой и плоскостью, равный углу между направляющим вектором прямой и проекцией этого вектора на координатную ось Oy.

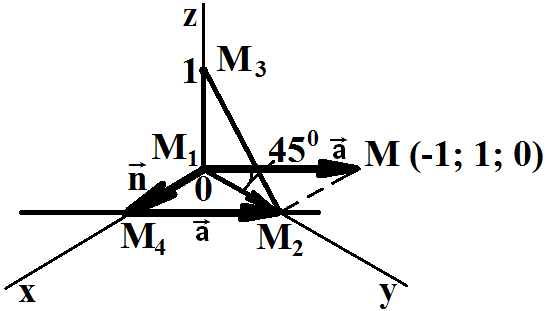
Ответ: угол между прямой и плоскостью φ = 45⁰.

Задача. В кубе ABCDA₁B₁C₁D₁ найдите угол между прямой BC₁ и плоскостью BCD₁.

37 Угол между двумя плоскостями

Две плоскости могут быть параллельны или пересекаться по прямой.

Угол между двумя пересекающимися плоскостями равен углу между двумя пересекающимися прямыми, проведенными перпендикулярно линии пересечения плоскостей.

Поэтому угол между плоскостями 0⁰ ≤ φ ≤ 90⁰.

Если заданы две плоскости

a₁x + b₁y + c₁z + d₁ = 0

и

a₂x + b₂y + c₂z + d₂ = 0,

то соответствующие нормальные векторы этих плоскостей ₁ (a₁; b₁; c₁) и ₂ (a₂; b₂; c₂). Косинус угла θ между нормальными векторами плоскостей

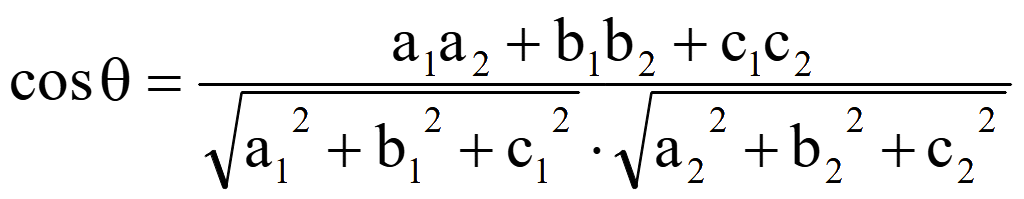
Если угол φ между плоскостями α и β равен углу θ между нормальными векторами этих плоскостей φ = θ, то

cos φ = cos θ.

Если угол между плоскостями φ = 180⁰ - θ, то

cos φ = cos (180⁰ - θ) = - cos θ.

cos φ = - cos θ.

Косинус угла между плоскостями

a₁x + b₁y + c₁z + d₁ = 0

и

a₂x + b₂y + c₂z + d₂ = 0

равен модулю косинуса угла между нормальными векторами ₁ (a₁; b₁; c₁) и ₂ (a₂; b₂; c₂) этих плоскостей

cos φ = |cos θ| =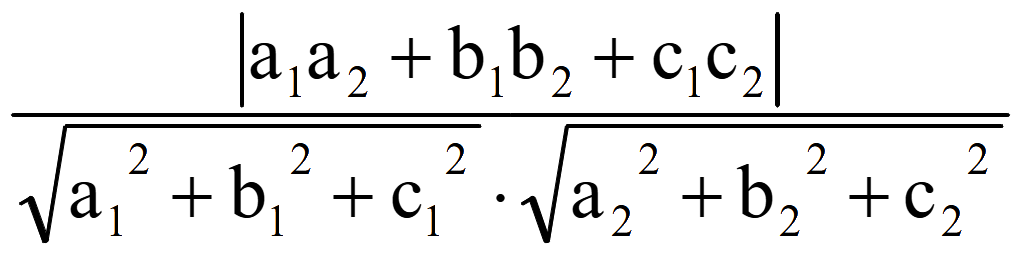

или можно записать так

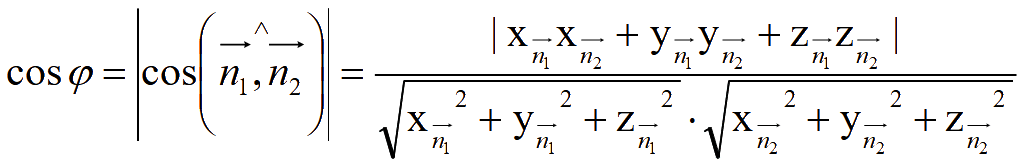
Для лучшего запоминания сформулируем следующее правило. Плоскости являются одинаковыми геометрическими объектами, поэтому и одинаковые тригонометрические функции cos присутствуют в формуле.

Косинус угла между плоскостями

cos φ =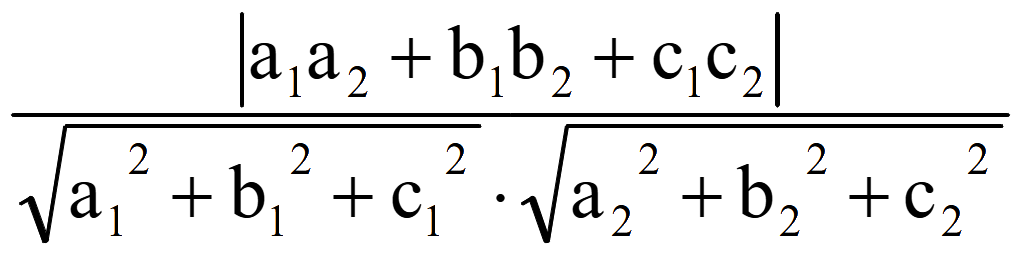

Угол между плоскостями

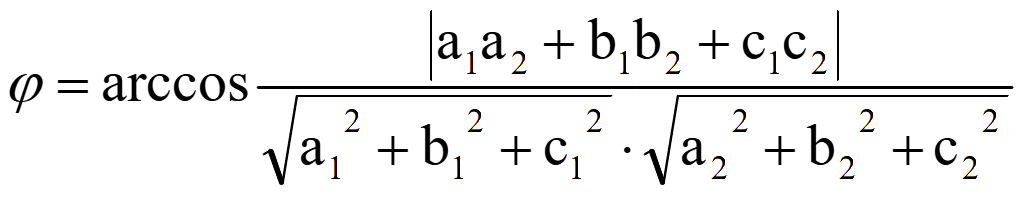
Если cos φ = 1, то угол φ между плоскостями равен 0⁰, можно принять для этих плоскостей один из нормальных векторов этих плоскостей, плоскости параллельны или совпадают. Если плоскости не совпадают, то они параллельны. Если плоскости совпадают, то любая точка одной плоскости принадлежит другой плоскости.

Если скалярное произведение нормальных ненулевых векторов ₁ (a₁; b₁; c₁) и ₂ (a₂; b₂; c₂) плоскостей равно нулю

a₁a₂ + b₁b₂ + c₁c₂ = 0

и, следовательно, cos φ = 0, то угол φ между плоскостями 90⁰ (плоскости перпендикулярны), плоскости пересекаются по прямой.

Если 0 ≤ cos φ < 1, то угол между плоскостями 0⁰ < φ ≤ 90⁰, плоскости пересекаются по прямой.

37.1 Алгоритм нахождения угла между двумя плоскостями

1. Задать систему координат с началом на линии пересечения плоскостей. Плоскости проходят через начало координат, поэтому d = 0.

2. В системе координат построить не менее двух точек, задающих каждую плоскость, между которыми требуется определить угол. Эти две точки необходимо задать так, чтобы прямая, соединяющая эти точки не проходила через начало координат.

3. Определить координаты заданных двух точек для каждой плоскости.

4. Задать один коэффициент уравнения плоскости равным 1, обычно принимается a = 1. Если какая-то координата равна 0, то принять за 1 необходимо коэффициент, соответствующий этой координате.

5. Составить систему двух уравнений для каждой из 2-х плоскостей. В каждой системе уравнений каждое уравнение соответствует каждой из 2-х точек на плоскости.

6. Решить системы уравнений и составить уравнения двух плоскостей, из которых определяются координаты двух нормальных векторов.

7. Косинус угла между плоскостями равен модулю косинуса угла между нормальными векторами этих плоскостей

cos φ = |cos θ| =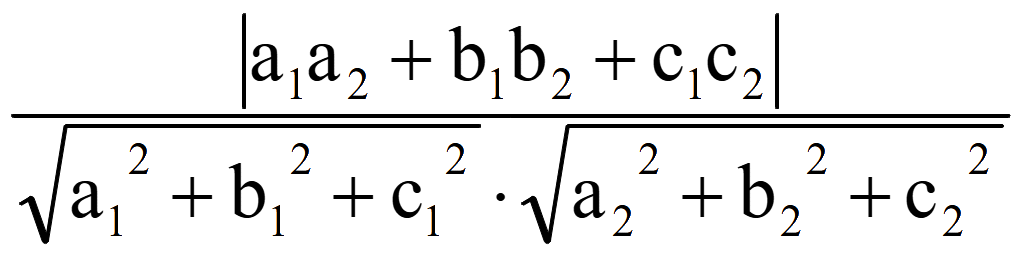

Задача. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ заданы ребра: AB = 16, AD = 14, СС₁ = 24. Найти угол между плоскостями ABC и A₁DB.

38 Углы между векторами, прямыми и плоскостями

Косинус угла θ между двумя ненулевыми векторами = (x₁; y₁; z₁) и = (x₂; y₂; z₂)

cos θ =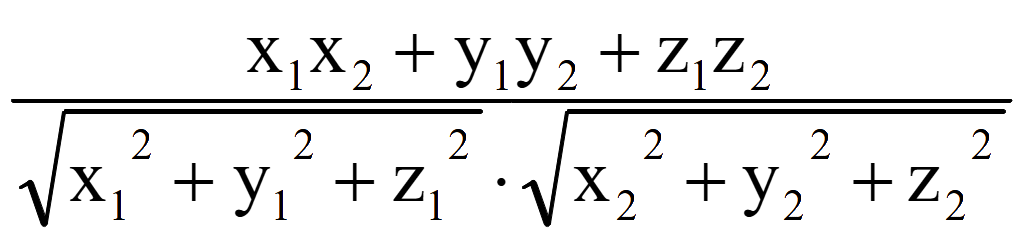

Косинус угла φ между двумя прямыми или двумя плоскостями

cos φ =

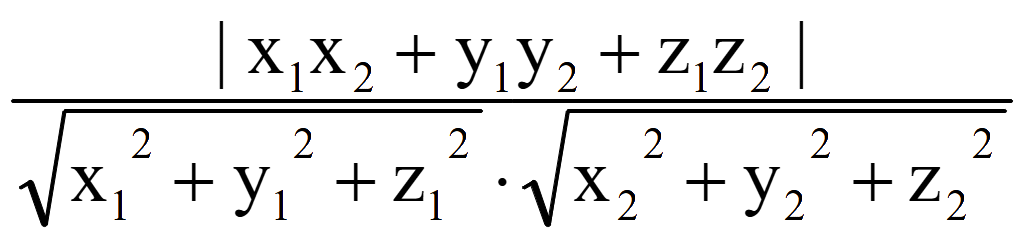
где θ — угол между направляющими векторами прямых или нормальными векторами плоскостей.

Угол φ между двумя прямыми или двумя плоскостями

φ = arccos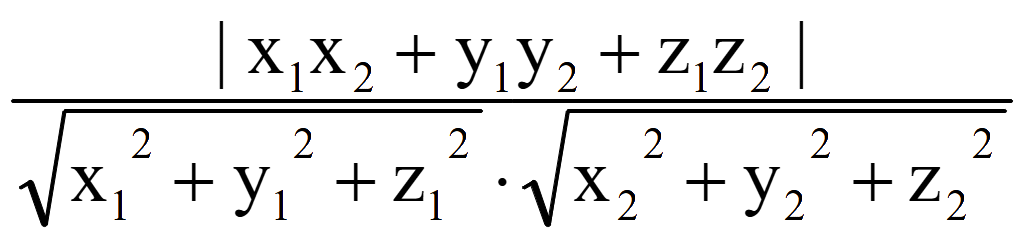

Синус угла φ между прямой и плоскостью

sin φ =

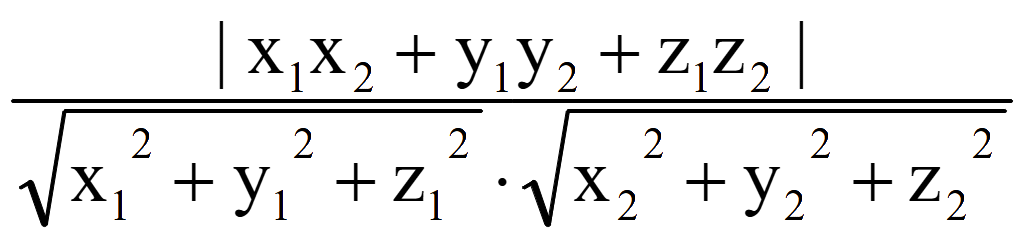
где θ — угол между направляющим вектором прямой и нормальным вектором плоскости.

Угол φ между прямой и плоскостью

φ = arcsin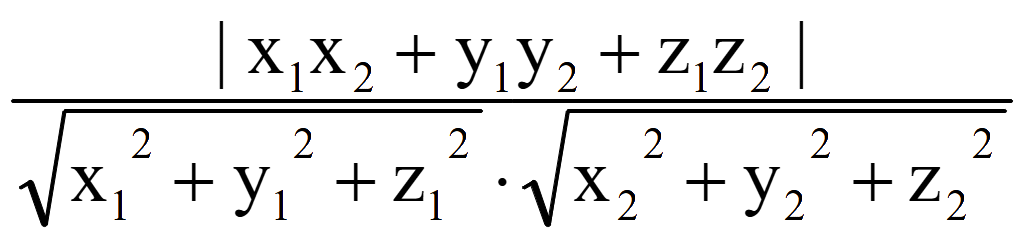

39 Расстояние от точки до плоскости

Если известны координаты точки M₀ (x₀; y₀; z₀) и уравнение плоскости ax + by + cz + d = 0 (a² + b² + c² ≠ 0, то есть a, b и c одновременно не равны нулю), то расстояние от данной точки до плоскости определяется следующим образом.

Проекцией точки M₀ на плоскость является точка M₁ (x₁; y₁; z₁), поэтому вектор перпендикулярен плоскости и коллинеарен нормальному вектору плоскости (a; b; c). Следовательно,

= k .

Так как координаты нормального вектора плоскости (a; b; c), то координаты коллинеарного вектора k (ka; kb; kc).

Координаты вектора равны разности координат конца и начала вектора = (x₁ - x₀; y₁ - y₀; z₁ - z₀), поэтому

= (x₁ - x₀; y₁ - y₀; z₁ – z₀) = k = (ka; kb; kc);

x₁ - x₀ = ka; y₁ - y₀ = kb; z₁ - z₀ = kc.

Отсюда

x₁ = ka + x₀; y₁ = kb + y₀; z₁ = kc + z₀.

Расстояние между точкой M₀ и плоскостью равно длине вектора , которая равна

| |= |k|| |

Длина нормального вектора равна корню квадратному из суммы квадратов его координат

| |= |k|

Подстановка координат точки M₁ (x₁; y₁; z₁) в уравнение плоскости дает равенство

ax₁ + by₁ + cz₁ + d = 0.

Подставляем полученные ранее значения x₁, y₁, z₁

a(ka + x₀) + b(kb + y₀) + c(kc + z₀) + d = 0

Путем преобразований выразим k. Раскроем скобки

ka² + ax₀ + kb² + by₀ + kc² + cz₀ + d = 0,

сгруппируем

ka² + kb² + kc² + ax₀ + by₀ + cz₀ + d = 0.

Вынесем k за скобку и перенесем члены, не содержащие k в правую часть равенства

k(a² + b² + c²) = -(ax₀ + by₀ + cz₀ + d).

Выразим k

Модуль k

Подставим |k|

| |=

| |=

| |=

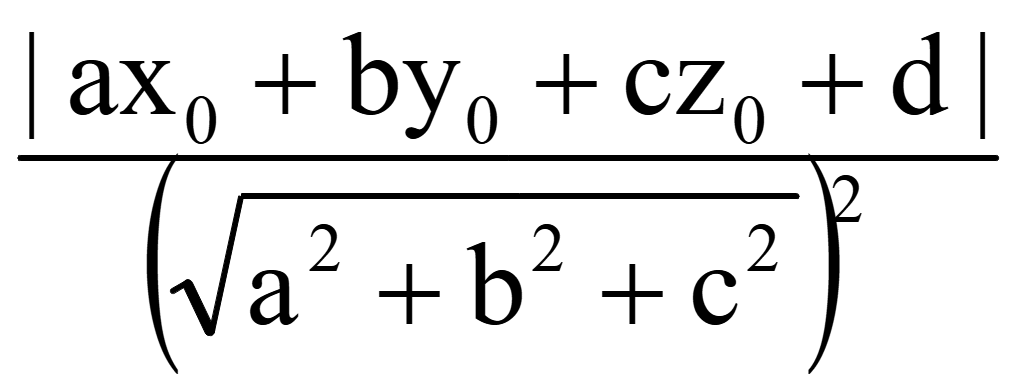
Расстояние от точки M₀ (x₀; y₀; z₀) до плоскости, заданной уравнением ax + by + cz + d = 0 (a² + b² + c² ≠ 0)

ℓ =

Расстояние между точкой и плоскостью равно модулю суммы произведений соответствующих координат нормального вектора и точки плюс d, деленного на длину (модуль) нормального вектора плоскости.

Другими словами расстояние между точкой и плоскостью равно модулю левой части уравнения плоскости, в которую подставили координаты точки, деленного на длину (модуль) нормального вектора плоскости.

Желательно выбрать систему координат так, чтобы искомая плоскость проходила через начало координат, а так же, чтобы заданная точка M₀ (x₀; y₀; z₀) находилась на одной из осей координат. Тогда решаемая задача значительно упрощается за счет того, что d и две координаты точки нулевые. Уравнение расстояния от точки до плоскости значительно упрощается

ℓ =

в этом уравнении два члена в числителе обнулятся и останется один член.

Если заданная точка M₀ (x₀; y₀; z₀) совпадает с ось Ox, то координаты y, z точки равны нулю и получаем простейшее уравнение искомого расстояния, содержащее лишь координату x точки

ℓ =

Таким образом, если точка совпадает с ось Ox, то в уравнении присутствует лишь координата x точки.

Если заданная точка M₀ совпадает с ось Oy, то координаты x, z точки равны нулю и получаем простейшее уравнение искомого расстояния

ℓ =

Таким образом, если точка совпадает с ось Oy, то используется лишь координата y точки.

Если заданная точка M₀ совпадает с ось Oz, то координаты x, y точки равны нулю и получаем простейшее уравнение искомого расстояния

ℓ =

Таким образом, если точка совпадает с ось Oz, то используется лишь координата z точки.

Задача. Все ребра правильной четырехугольной пирамиды SABCD равны 1. Найти расстояние между плоскостью SAD и серединой ребра AB.

Задача. Определить общее уравнение плоскости

ax + by + cz + d = 0,

проходящей через точки M₁ (1; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1). Найти расстояние от этой плоскости до точки M₀ (10; -3; -7).

Решение

Построим заданные точки M₁ (1; 0; 0), M₂ (0; 1; 0) и M₃ (0; 0; 1) в системе координат Oxyz.

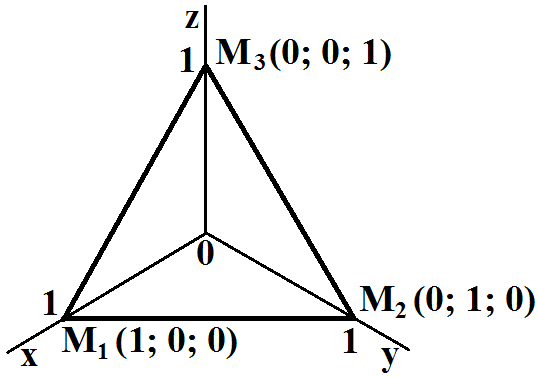
Примем a = 1. Подстановка координат трех точек в общее уравнение плоскости дает систему 3-х уравнений

; ;

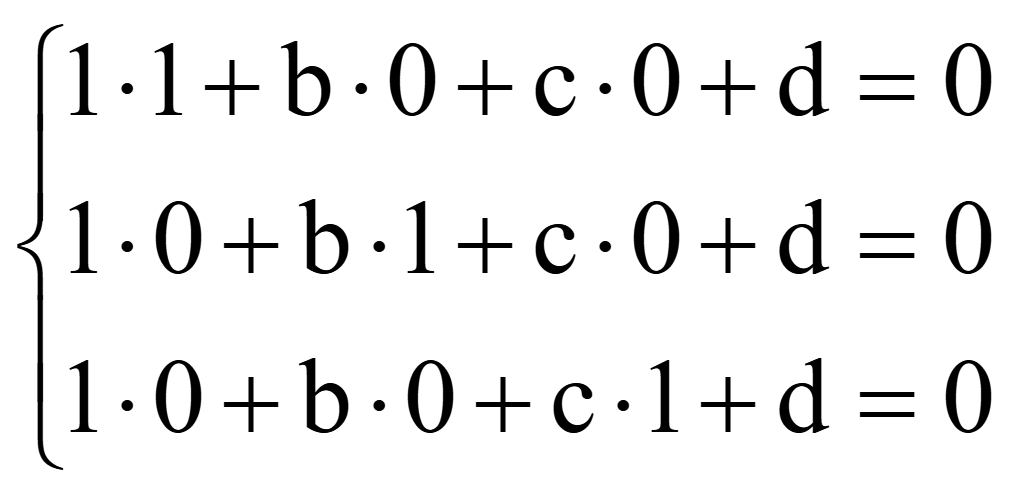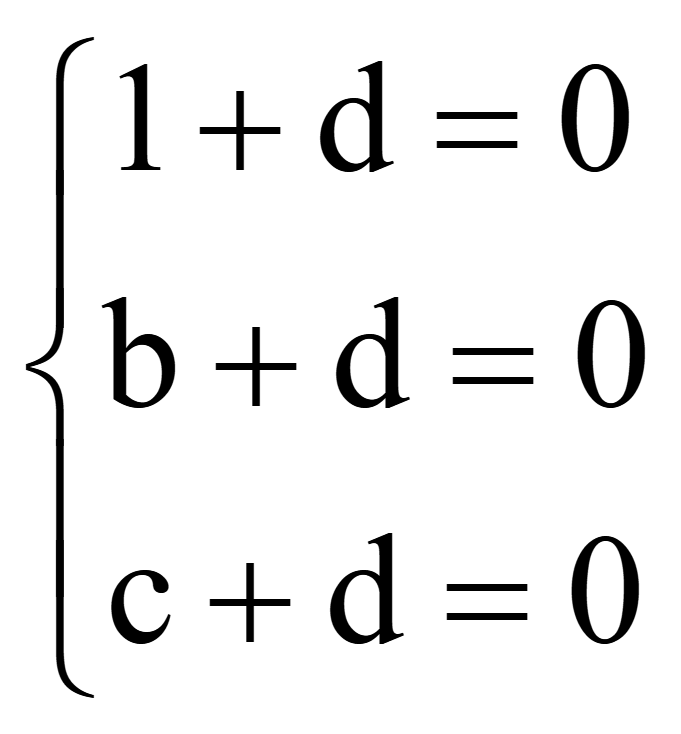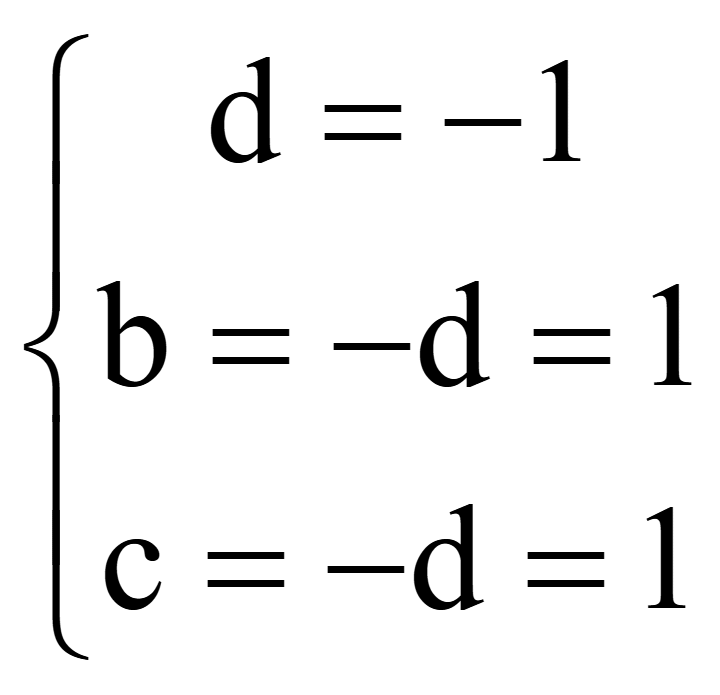
Координаты нормального ненулевого вектора плоскости (1; 1; 1), в изображенной ранее системе координат он будет изображен точкой, поэтому покажем проекции нормального вектора на плоскости xOy, yOz, xOz.

Общее уравнение плоскости

x + y + z - 1 = 0.

Расстояние от точки M₀ до плоскости

ℓ =

ℓ =

40 Расстояние между двумя параллельными плоскостями

Плоскости параллельны, поэтому у них коллинеарные или равные нормальные векторы. Для параллельных плоскостей можно записать уравнения с равными коэффициентами a, b, c, одновременно не равными нулю (a² + b² + c² ≠ 0) и являющимися координатами нормального вектора одной из параллельных плоскостей

ax + by + cz + d₁ = 0;

ax + by + cz + d₂ = 0.

Достаточно определить расстояние от точки M₀ (x₀; y₀; z₀) в какой-то плоскости до другой плоскости, заданной уравнением

ax + by + cz + d = 0

по ранее выведенной формуле

ℓ =

Если в условии задачи сказано, что плоскости параллельны, и требуется определить расстояние между этими плоскостями, то необходимо определить нормальный вектор (уравнение) одной из плоскостей, а также координаты точки в другой плоскости. Желательно для значительного упрощения задачи так задать систему координат, чтобы максимальное количество геометрических объектов совпадало с началом координат и осями координат.

Векторы на плоскости и в пространстве веб-страницы: 1 2 3

© 03.06.21 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru