© 2021 Ольшевский Андрей Георгиевич репетитор по физике, математике, информатике, авиации, двигателям, электронике, искусственному интеллекту, программированию, техническим дисциплинам по Скайп da.irk.ru
Сайт super-code.ru наполняется полезными темами, которые можно бесплатно сохранить
Оглавление
1.2 Напряженность электрического поля 5
1.3 Работа по перемещению заряда 13
1.4 Потенциал электростатического поля 15
1.5.1 Последовательное соединение конденсаторов 18
Репетитор по физике для студентов и школьников, ЕГЭ, ОГЭ
1.7 Сопротивление проводника тока 23
1.8 Закон Ома для участка цепи 23
1.9 Последовательное соединение сопротивлений 24
1.10 Параллельное соединение сопротивлений 28
1.11 Смешанное соединение сопротивлений 31
1.12 Источник тока. Закон Ома для замкнутой полной цепи 39
Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru 99
По закону Кулона действующая на заряды сила Кулона
![]() ,
,
где k – коэффициент пропорциональности, k = 9·109 Н·м2/Кл2;
q1 – заряд первого тела, Кл;
q2 – заряд второго тела, Кл;
r – расстояние между зарядами, м.
Одноименные заряды отталкиваются, разноименные заряды притягиваются. Сила Кулона пропорциональна изменению заряда, изменяется обратно пропорционально квадрату расстояния между зарядами. Увеличение расстояния в 2 раза приводит к уменьшению силы в 4 раза. Уменьшение расстояния в 3 раза приводит к увеличению силы Кулона в 9 раз.
Задание А11 [9 (ЕГЭ 2014 Демо)]

Решение
После соединения шаров электрометров общий заряд системы равен сумме зарядов
qА + qБ = -3 + 1 = -2.
Но так как электрометра два, то заряд распределится между ними поровну и каждый приобретет заряд -1. Стрелки электрометров покажут одинаковое значение 1.
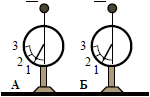
Ответ: 2) станут равными 1.
Напряженность электрического поля, создаваемая зарядом q1
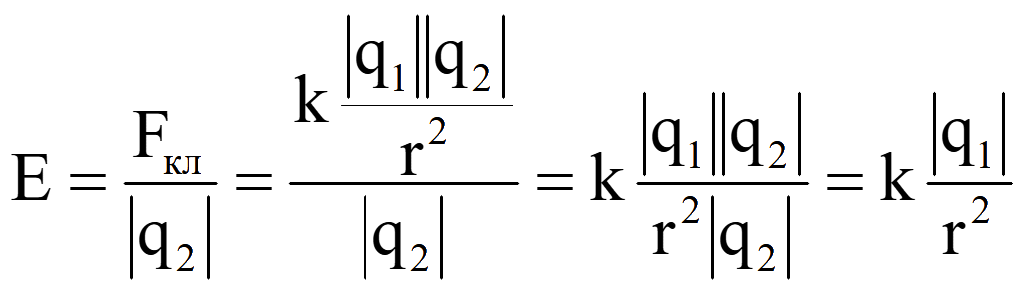
![]()
Формула напряженности электрического поля содержит в числителе один заряд.
Вектор напряженности электрического поля направлен от плюса к минусу. На рисунке вектор напряженности направлен от положительно заряженной пластины к отрицательной
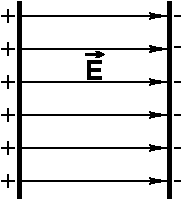
Вектор электрического поля диполя направлен против вектора внешнего электрического поля, вызвавшего образование диполя.
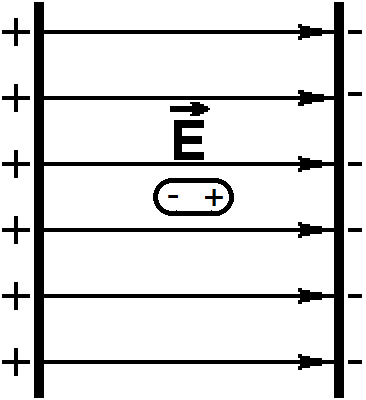
Если присутствует лишь положительный заряд, то вектор напряженности электрического поля направлен от плюса. Если имеется лишь отрицательный заряд, то вектор напряженности электрического поля направлен к минусу.
Размерность напряженности
![]()
Если в электрическое поле, создаваемое зарядом q1 помещать другие заряды, то напряженность электрического поля заряда q1 не изменится, но величина помещаемого заряда будет влиять на значение силы, действующей на помещенный в электрическое поле заряд q. Сила Кулона, действующая на заряд q, помещенный в электрическое поле E
![]() .
.
Если в электрическое поле помещен положительный заряд, то сила Кулона сонаправлена с вектором напряженности электрического поля. Вектор силы Кулона, действующей на отрицательный заряд направлен в сторону, противоположную вектору напряженности электрического поля. Знак заряда влияет на направление вектора силы Кулона
![]()
![]()
Напряженность электрического поля, вызванная несколькими зарядами, подчиняется принципу суперпозиции: каждый заряд в данной точке создает свой не зависящий от других зарядов вектор напряженности. Результирующий вектор напряженности равен векторной сумме напряженностей, вызванных каждым зарядом
![]()
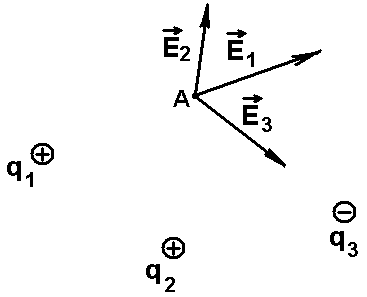
Пример. Определить напряженность в точке A.
![]()
Согласно принципу суперпозиции первый заряд вызывает напряженность в точке A, вектор которой направлен от положительного заряда
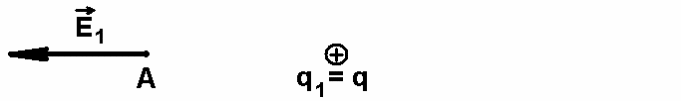
Второй заряд вызывает напряженность в точке A, вектор которой направлен к отрицательному заряду.

Длина
вектора напряженности
![]() меньше длины вектора напряженности
меньше длины вектора напряженности
![]() ,
так как расстояние от заряда q2
до точки A
гораздо больше расстояния от q1
до A.
Длина вектора напряженности (модуль напряженности) обратно
пропорциональна квадрату расстояния от заряда до точки, в которой
необходимо определить напряженность. То есть, если расстояние
увеличивается в 2 раза, то длина вектора напряженности уменьшается в
4 раза. Если расстояние от заряда до точки увеличивается в 3 раза, то
длина вектора напряженности уменьшается в 9 раз.
,
так как расстояние от заряда q2
до точки A
гораздо больше расстояния от q1
до A.
Длина вектора напряженности (модуль напряженности) обратно
пропорциональна квадрату расстояния от заряда до точки, в которой
необходимо определить напряженность. То есть, если расстояние
увеличивается в 2 раза, то длина вектора напряженности уменьшается в
4 раза. Если расстояние от заряда до точки увеличивается в 3 раза, то
длина вектора напряженности уменьшается в 9 раз.
В итоге векторы напряженностей в точке A
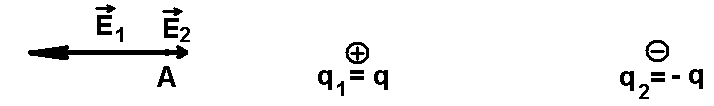
Результирующий
вектор напряженности равен векторной сумме
![]()
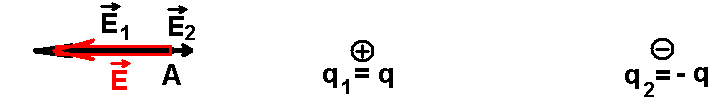
Пример. Определим напряженность в точке А, находящейся на одинаковом расстоянии от одинаковых по модулю зарядов
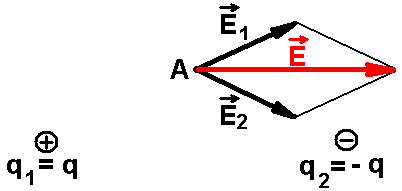
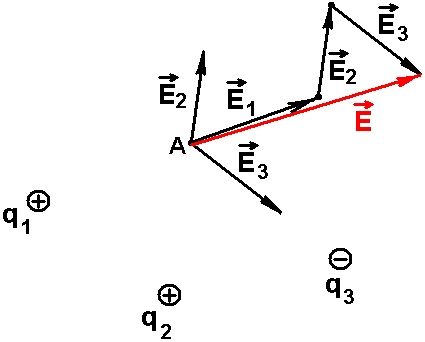
Пример. Определим напряженность в точке А
Результирующий
вектор напряженности равен векторной сумме
![]()
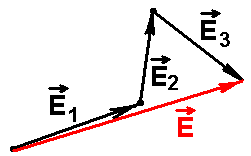
Сложим вектора по правилу многоугольника
Задача. Найдите силу, действующую на заряд 2 нКл, расположенный вблизи заряженной плоскости с поверхностной плотностью заряда 20 мкКл/м2.
Дано: q = 2 нКл = 2·10-9 Кл, σ = 20 мкКл/м2 = 20· 10-6 Кл/м2.
Решение
Напряженность электростатического поля бесконечной плоскости в вакууме определяется по формуле:
![]() ,
,
где E – напряженность, Н/Кл;
σ — поверхностная плотность заряда, Кл/м2;
ε0 — электрическая постоянная.
![]()
Сила, действующая на заряд, расположенный вблизи заряженной плоскости
![]()
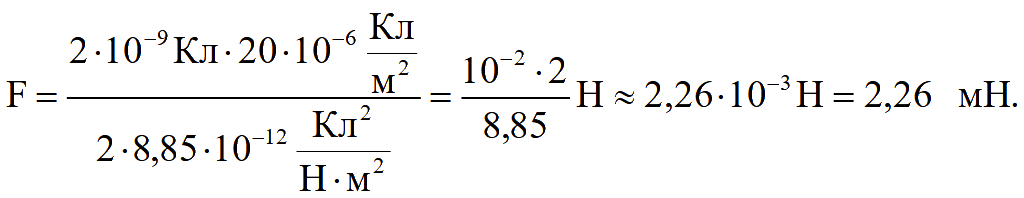
Ответ: F = 2,26 мН.
Задача С2 [2; стр 55] Полый металлический шарик массой 5 г подвешен на шелковой нити длиной 120 см. Шарик имеет положительный заряд 10-8 Кл и находится в однородном электрическом поле напряженностью 106 В/м. Вектор напряженности поля направлен вертикально вниз. Чему равен период малых колебаний шарика?
Дано: m = 5 г = 5·10-3 кг, ℓ = 120 см = 1,2 м; q = 10-8 Кл; E = 106 В/м. T - ?
Решение
Период колебаний математического маятника
![]() (1)
(1)
Рассчитаем сначала период колебаний металлического шарика, не помещая его в электрическое поле.
![]()
Если положительно заряженный металлический шарик поместить в однородное электрическое поле, вектор напряженности которого направлен вертикально вниз, то на шарик будет действовать сила, также направленная вниз
F = Eq = 106 ·10-8 = 10-2 Н
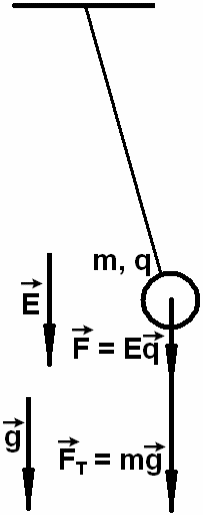
На шарик массой m = 5·10-3 кг будет действовать сила тяжести
Fт = mg = 5 ·10-3 ·10 = 5 ·10-2 Н
Сумма сил, действующих на шарик вниз
F + Fт = Eq + mg = 10-2 + 5 ·10-2 = 6 ·10-2 Н
По второму закону Ньютона сумма сил равна ma:
![]()
F + Fт = ma
Отсюда ускорение
![]()
Это ускорение подразумевает увеличение за счет электростатических сил ускорения свободного падения шарика (если нить обрезать, то шарик будет падать вниз с большим ускорением). Подставляем это ускорение вместо ускорения свободного падения в формулу периода колебаний (1)
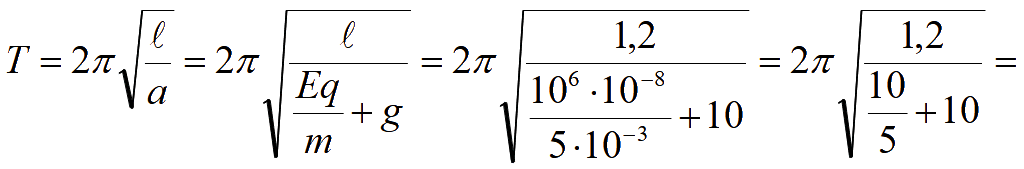
![]()
Электрическое поле увеличивает ускорение, с которым свободный положительно заряженный шарик падал бы вниз, поэтому период колебаний подвешенного на нити шарика уменьшается с 2,18 с до 2с.
Ответ: T ≈ 2 с.
Между заряженными пластинами возникает электростатическое поле, вектор напряженности которого направлен от положительной к отрицательной пластине. На положительный заряд, помещенный в электрическое поле действует сила Кулона сонаправленная с вектором напряженности поля, так как положительный заряд отталкивается от положительно заряженной пластины и притягивается к отрицательно заряженной пластине.
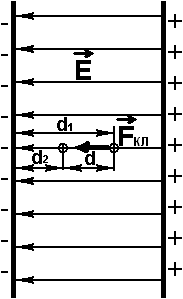
Работа по перемещению положительного заряда q в электростатическом поле напряженностью E на расстояние d = d1 - d2:
A = Fклd = qEd = qE(d1 – d2) = -(qEd2 - qEd1)
где d1 и d2 – начальное и конечное расстояния до отрицательной пластины, м.
В формуле
A = qEd
знак работы совпадает со знаком заряда, если перемещение заряда происходит в направлении напряженности электрического поля. Электрическое поле при перемещении положительного заряда в направлении вектора напряженности совершает положительную работу.
Потенциальная энергия заряженной частицы равна возможной работе силы Кулона
Eп = |q|Ed,
где d – расстояние от заряженной частицы до точки с нулевой потенциальной энергией, м.
Положительная работа по перемещению заряда в электрическом поле происходит за счет уменьшения потенциальной энергии:
A = - (Eп2 — Eп1) = - ΔEп
Положительная работа по перемещению положительного заряда совершается в направлении вектора напряженности электрического поля за счет уменьшения потенциальной энергии этого заряда.
Если потенциальную энергию, действующую на заряд q, разделить на величину этого заряда, то получим потенциал потенциального электростатического поля с напряженностью E, создаваемого зарядом q1
![]() ,
,
где d – расстояние от заряда q1 до точки, в которой определяется потенциал.
Потенциал, создаваемый зарядом q
![]()
Знак потенциала равен знаку заряда, создающего потенциал в точке, удаленной от заряда на расстояние d.
Формула потенциала электрического поля содержит в числителе один заряд так же как и напряженность, но в знаменателе расстояние без квадрата.
Сила Кулона |
Напряженность |
Потенциал |
|
|
|
Потенциальная энергия связана с потенциалом посредством коэффициента q:
Eп = qφ
A = - (Eп2 — Eп1) = - (qφ2 — qφ1) = -q(φ2 — φ1) = q(φ1 — φ2) = qU,
где разность потенциалов φ1 — φ2 = U есть напряжение, В.
Напряжение (разность потенциалов)
![]()
где d – расстояние между точками с разными потенциалами, м.
![]()
![]()
Потенциал так же как и потенциальная энергия величина не векторная, а скалярная. Уменьшение потенциальной энергии происходит в направлении напряженности электрического поля и сопровождается уменьшением потенциала. Вектор напряженности электрического поля указывает куда убывает потенциал.
Эквипотенциальными называют поверхности с равным потенциалом, поэтому вектор напряженности перпендикулярен эквипотенциальным поверхностям.
Для определения потенциала, создаваемого зарядами в точке поля, необходимо просуммировать потенциалы, создаваемые каждым зарядом в данной точке поля, с учетом знаков потенциалов, совпадающих со знаком, вызвавших их зарядов.
Ёмкость конденсатора
![]()
q – заряд одной из пластин конденсатора, Кл;
U – напряжение между обкладками конденсатора, В.
Ёмкость конденсатора
![]()
где ε0 — электрическая постоянная, которую можно определить из коэффициента пропорциональности в законе Кулона
![]()
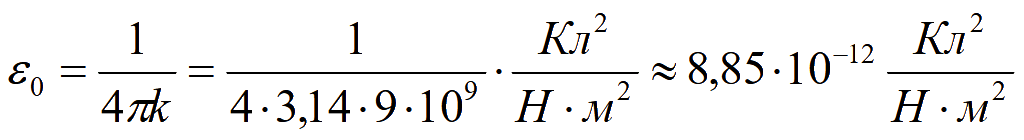 ;
;
ε — относительная диэлектрическая проницаемость среды между пластинами конденсатора (в вакууме ε = 1, для воздуха можно принять ε=1);
S – площадь меньшей из пластин конденсатора (площадь перекрытия пластин), м2;
d – расстояние между пластинами, м.
Энергия электрического поля конденсатора (потенциальная энергия) определяется с учетом взаимодействия заряда на одной пластине q и напряженности электрического поля, создаваемой другой пластиной конденсатора, которая в 2 раза меньше напряженности между 2-мя пластинами конденсатора:
![]() .
.
При последовательном соединении конденсаторов
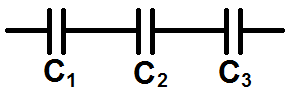
Эквивалентная емкость батареи n конденсаторов
![]()
Эквивалентная емкость батареи из 2-х конденсаторов
![]()
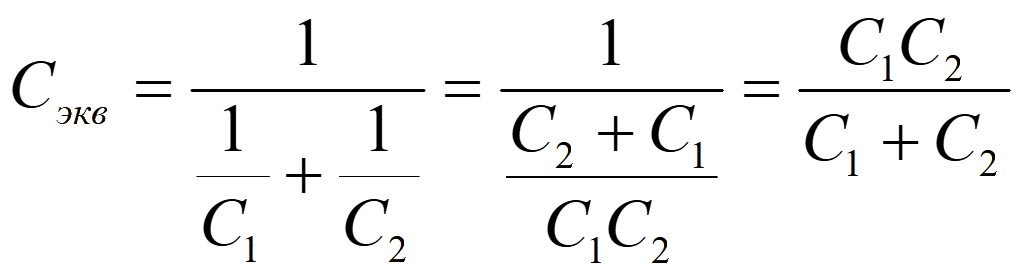
![]()
Эквивалентная емкость батареи из 3-х конденсаторов
![]()
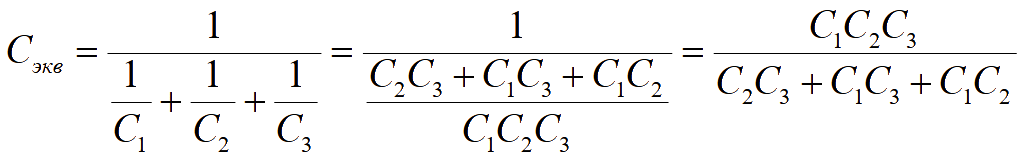
![]()
Задача. Определить эквивалентную емкость батареи последовательно соединенных конденсаторов. Определить общий заряд батареи конденсаторов. Определить разность потенциалов между обкладками каждого конденсатора.
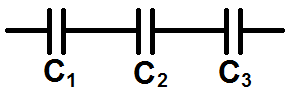
![]()
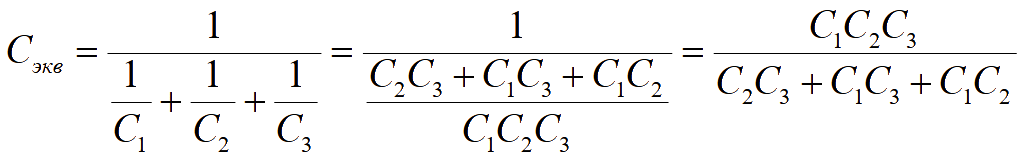
![]()
Подставим значения
![]()
![]()
![]()
2 способ
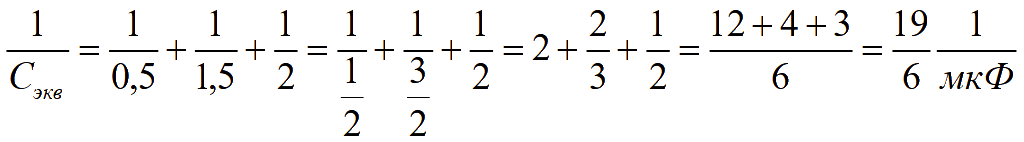
![]()
Общий заряд батареи последовательно соединенных конденсаторов
q = CU
![]()
![]()
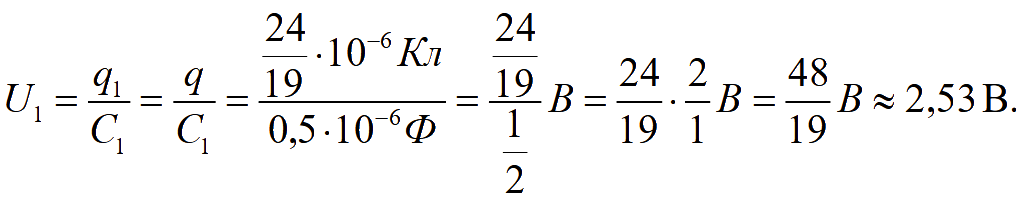
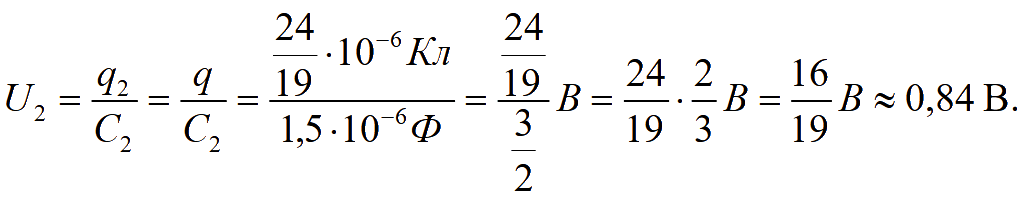
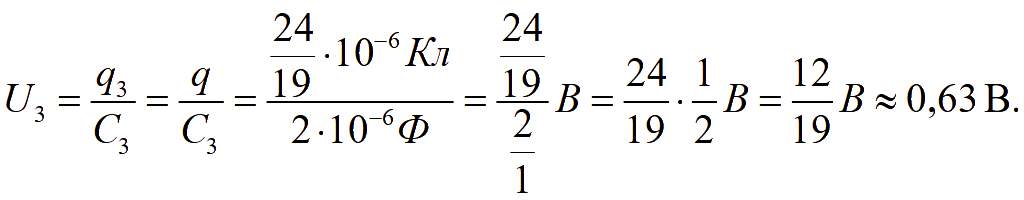
При последовательном соединении конденсаторов напряжение батареи конденсаторов равно сумме напряжений на обкладках каждого конденсатора
U = U1 + U2 + U3;
![]()
Верно!
За положительное направление тока принято движение положительных зарядов (от плюса источника питания по внешней цепи к минусу). В металлах фактически движутся отрицательно заряженные электроны против положительного направления тока.
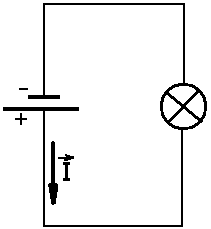
Сила тока I вычисляется по формуле
![]() ,
,
где I – сила тока, А (Ампер);
Δq – количество зарядов, прошедших по проводнику, Кл (Кулон);
Δt – промежуток времени, с.
Сила тока есть отношение заряда q, переместившегося через сечение проводника за время t
![]()
Сила тока равна производной заряда по времени и фактически характеризует скорость протекания зарядов через сечение проводника
![]()
В объеме проводника между сечениями SΔt с количеством зарядов q0 в единице объема n (концентрацией зарядов) содержится заряженных частиц
![]()
Общий заряд этих частиц
![]() ,
,
где
n
– концентрация (количество частиц в единице объема),
![]() .
.
Если скорость протекания зарядов по проводнику
![]() ,
,
то за время
![]()
через сечение 2 протекут все заряды, которые были заключены между сечениями 1 и 2
![]()
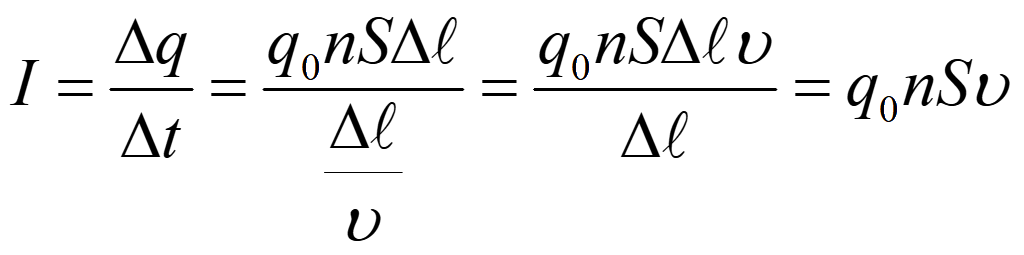
Скорость распространения начала движения зарядов по проводнику (возбуждения) равна скорости света, но сами электроны движутся значительно медленнее (0,6 — 6 мм/с).
Определим время прохождения тока от Москвы до Иркутска
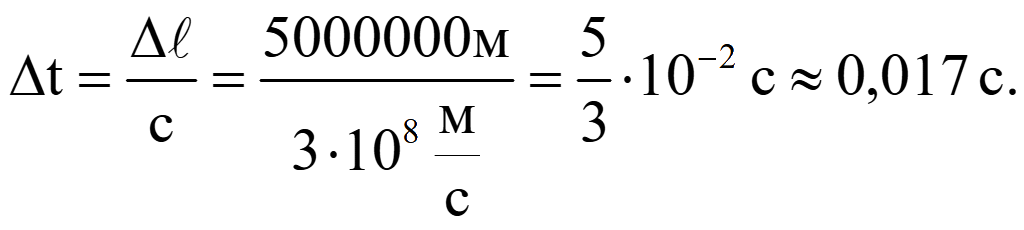 .
.
Сопротивление проводника, Ом
![]() ,
,
где ρ - удельное сопротивление, Ом·м2/м = Ом·м, Ом·мм2/м;
ℓ - длина проводника, м;
S – площадь, м2, мм2.
Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению:
![]() ;
;
U = IR;
![]() .
.
![]()
Сопротивление всей цепи равно сумме сопротивлений отдельных участков
R = R1 + R2 + R3 + … (1)
Количество зарядов, протекающих через участки цепи в единицу времени остается неизменным. Поэтому сила тока в цепи равна силе тока на каждом участке цепи:
I = I1 = I2 = I3 = …
Следовательно амперметр включается последовательно в цепь.
Помножив обе части равенства (1) на I, получим
IR = IR1 + IR2 + IR3 + … (2)
По закону Ома напряжение всей цепи
U = IR
Разность потенциалов (падение напряжения) на первом сопротивлении
U1 = IR1
Падения напряжений на сопротивлениях 2 и 3
U2 = IR2
U3 = IR3
Получим из (2) уравнения
U = U1 + U2 + U3 + …
Напряжение на выводах цепи равно сумме падений напряжения на каждом участке цепи. Поэтому вольтметр включается параллельно сопротивлению.
Формулу для напряжений можно вывести 2-м способом. По закону Ома
![]()
Заменив сопротивления в равенстве (1) получим
![]()
![]()
![]()
Помножив обе части равенства на I, после сокращения получим
U = U1 + U2 + U3 + …
Помножим обе части равенства на I
IU = IU1 + IU2 + IU3 + …
Произведение силы тока и напряжения равно мощности
N = IU
Мощность цепи последовательно соединенных элементов равна сумме мощностей отдельных элементов
N = N1 + N2 + N3 + …
Мощность может быть определена различными способами
![]()
Задача № 14 [10 (Демо ГИА 2014)]. В сеть с напряжением 120 В последовательно с лампой включён реостат. Напряжение на реостате 75 В. Каково сопротивление лампы, если сила тока в цепи равна 12 А?
Дано: U = 120 В; UR = 75 В; I = 12 А. Rл - ?
Решение
Схема цепи:
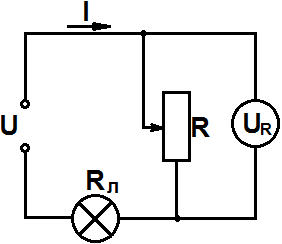
При последовательном соединении сила тока одинакова во всех участках цепи и равна I. Напряжение в цепи равно сумме падений напряжений на отдельных участках цепи
U = UR + Uл.
Отсюда падение напряжения на лампе
Uл = U - UR = 120 - 75 = 45 В.
Из закона Ома для участка цепи, содержащего лампу
![]()
выразим сопротивление лампы, Ом
![]()
Ответ: Rл = 3,75 Ом.
Задача
Дано: последовательно соединенные сопротивления R1 = 15 Ом; R2 = 10 Ом; мощность на первом резисторе P1 = 540 Вт.
Найти: Rэкв, U, U1, U2, I1, I2, P, P1, P2.
Решение
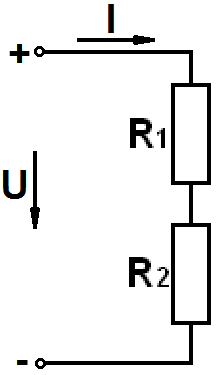
Сопротивление цепи последовательных сопротивлений равно сумме сопротивлений
Rэкв = R1 + R2 = 15 Ом + 10 Ом = 25 Ом.
Мощность на первом резисторе
P1 = I1U1 = I12R1.
Отсюда сила тока
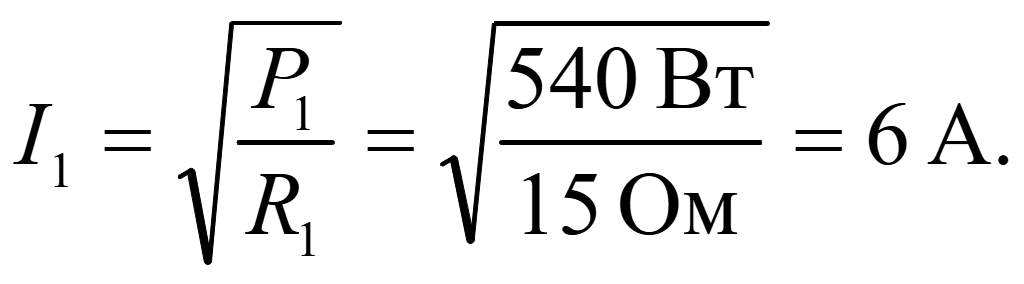
Сила тока в цепи последовательно соединенных сопротивлений равна силе тока на каждом участке цепи:
I = I1 = I2 = 6 А.
Из закона Ома для участка цепи напряжение
U = IRэкв = 6 А · 25 Ом = 150 В.
U1 = IR1 = 6 А · 15 Ом = 90 В.
U2 = IR2 = 6 А · 10 Ом = 60 В.
Произведение силы тока и напряжения равно мощности
P = IU = 6 А · 150 В = 900 Вт.
P2 = I2U2 = 6 А · 60 В = 360 Вт.
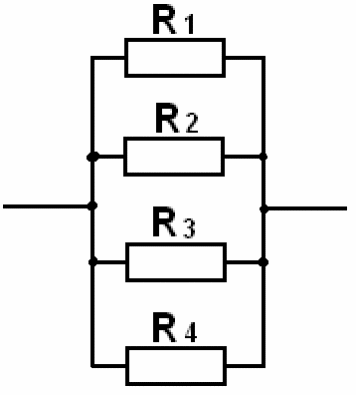
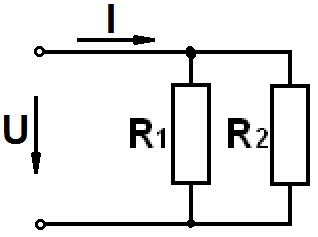
Разность потенциалов на концах сопротивлений равна
U = U1 = U2 = U3 … (1)
Заряды, протекающие по проводнику в месте разветвления цепи разделяются и текут отдельно по каждой ветви. Поэтому сила тока в не разветвленной цепи равна сумме сил тока в каждой ветви:
I = I1 + I2 + I3 + … (2)
По закону Ома для всей цепи
![]() ,
,
для отдельных ветвей закон Ома
![]() ,
,
![]()
После подстановки в уравнение (2)
![]() ,
,
![]() .
.
Сократим напряжение. Величина, обратная сопротивлению (проводимость) всей цепи равна сумме проводимостей отдельных участков
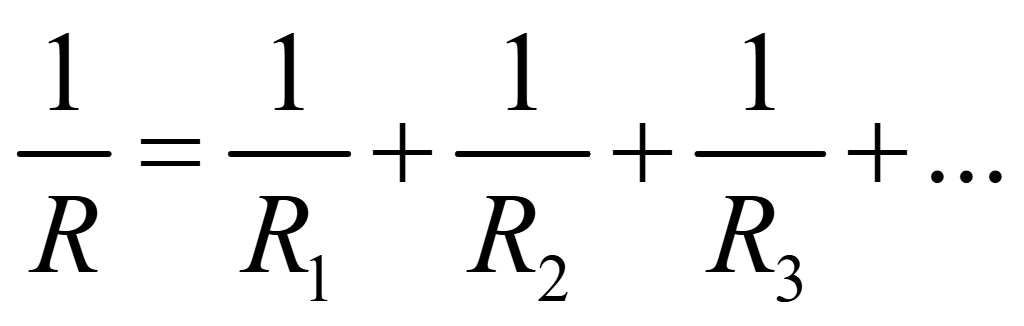 ,
,
отсюда сопротивление всей цепи (эквивалентное сопротивление)
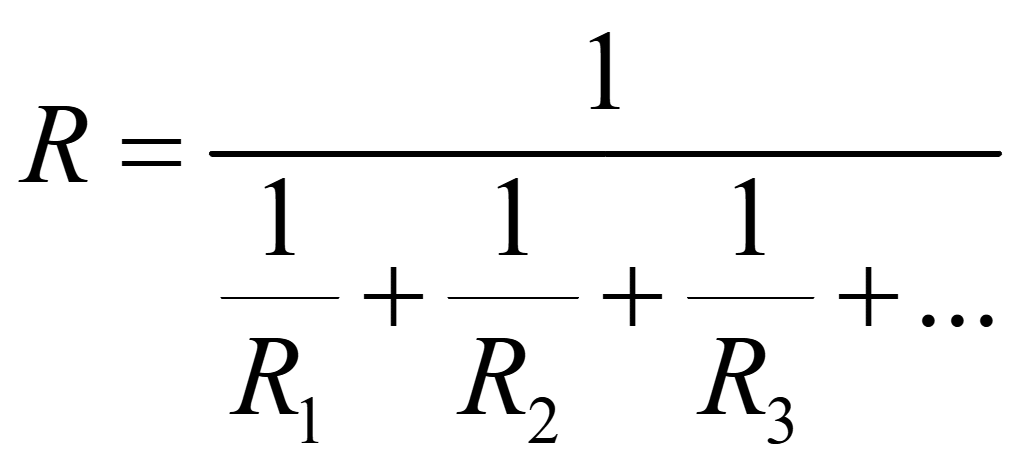 .
.
Эквивалентное сопротивление двух параллельных сопротивлений
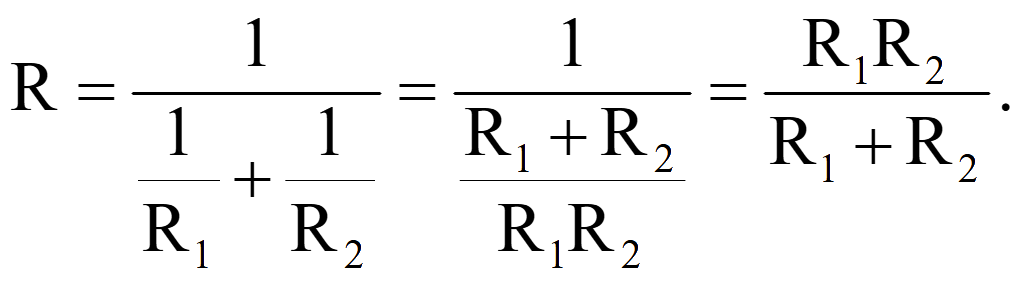
![]()
Эквивалентное сопротивление трех параллельных сопротивлений
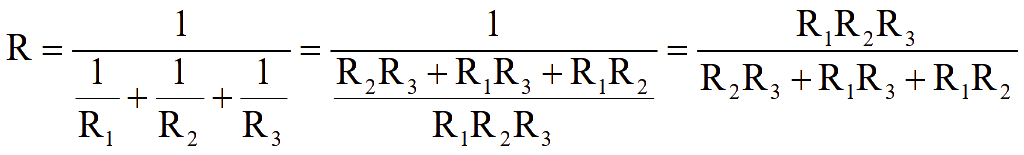
Помножим обе части равенства (2) на U
IU = I1U + I2U + I3U + …
Мощность цепи параллельно соединенных элементов равна сумме мощностей отдельных элементов
N = N1 + N2 + N3 + …
Мощности суммируются при последовательном и параллельном соединениях.
Задача
Дано: параллельно соединенные сопротивления R1 = 15 Ом; R2 = 10 Ом; ток в цепи I = 25 А.
Найти: Rэкв, U, U1, U2, I1, I2, P, P1, P2.
Решение
Величина, обратная сопротивлению (проводимость) параллельно соединенных сопротивлений равна сумме проводимостей отдельных участков
![]()
отсюда сопротивление всей цепи (эквивалентное сопротивление) двух параллельных сопротивлений
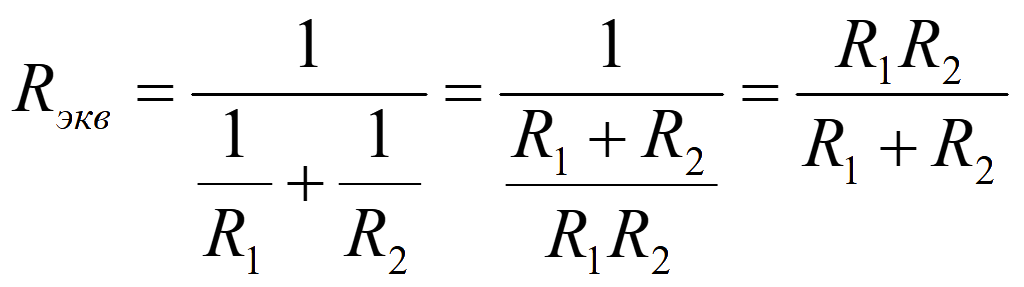
![]()
![]()
Из закона Ома для участка цепи напряжение
U = IRэкв,
U = 25 А · 6 Ом = 150 В.
Разность потенциалов на концах сопротивлений равна
U = U1 = U2 = 150 В.
По закону Ома для участка цепи сила тока
![]()
![]()
Произведение силы тока и напряжения равно мощности
P = IU = 25 А · 150 В = 3750 Вт = 3,75 кВт.
P1 = I1U1 = 10 А · 150 В = 1500 Вт = 1,5 кВт.
P2 = I2U2 = 15 А · 150 В = 2250 Вт = 2,25 кВт.
При последовательном (или параллельном) соединении сила тока в цепи равна силе тока в ветвях (или равна сумме сил тока в ветвях), напряжение в цепи равно сумме напряжений в ветвях (или равно напряжению в ветвях), сопротивление равно сумме сопротивлений (или обратная величина сопротивления равна сумме обратных величин сопротивлений в ветвях), мощность цепи всегда равна сумме мощностей в ветвях цепи.
При смешанном соединении сопротивлений сначала рассчитываются эквивалентные сопротивления параллельных соединений, затем эквивалентное сопротивление полученного последовательного соединения сопротивлений.
Пример. Рассчитать эквивалентное сопротивление цепи
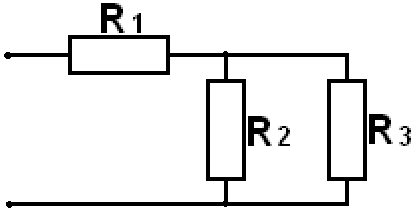
Сначала найдем эквивалентное сопротивление параллельных сопротивлений
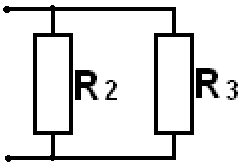
Величина, обратная сопротивлению (проводимость) параллельных сопротивлений равна сумме проводимостей отдельных участков
![]() ,
,
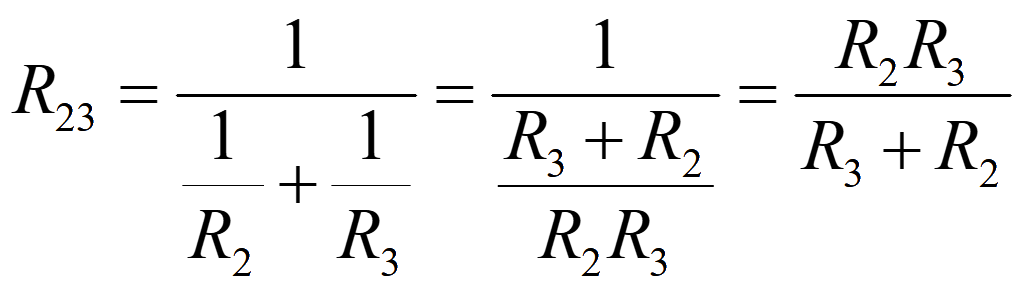
Получили эквивалентную цепь из последовательно соединенных сопротивлений
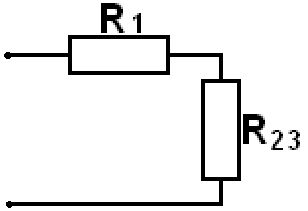
Эквивалентное сопротивление всей цепи
R123 = R1 + R23
![]()
Упражнение 23 [12 (Перышкин 8 кл. 2009)].

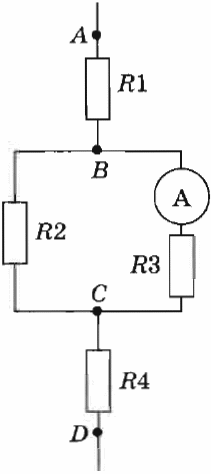
Дано:
R1 = 4 Ом; R2 = 6 Ом; R3 = 12 Ом; R4 = 2 Ом; I3 = 1 A. Найти: UBC , I1, I2, I4.
Решение
UBC = U2 = U3 = I3R3 = 1 A · 12 Ом = 12 В.
U2 = I2R2,
отсюда
![]()
Сила тока в цепи
I = I2 + I3 = I1 = I4 = 2 А + 1 А = 3 А
Задача. Сопротивление какой цепи, составленной из сопротивлений R, будет больше?
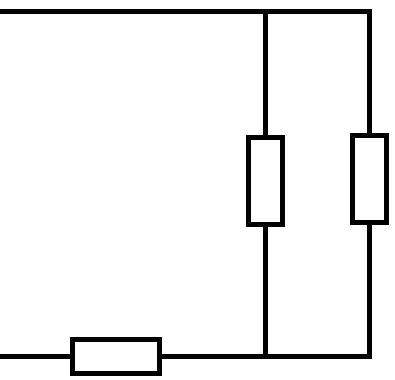
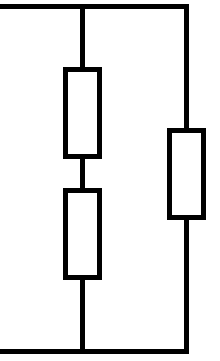
Решение
Сопротивление первой цепи
![]()
![]()
Ответ: Сопротивление 1 цепи будет больше.
Задача № 1381 [6].
![]()
Дано: R1 = R2 = R3 = R4 = R5 = R = 2 Ом. Rэкв - ?
Решение
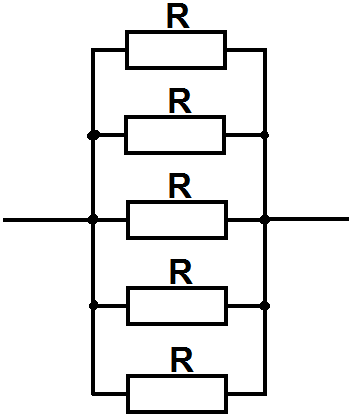
При параллельном соединении
![]()
![]()
![]()
![]()
Ответ: Rэкв = 0,4 Ом.
Задача № 1385 [6].

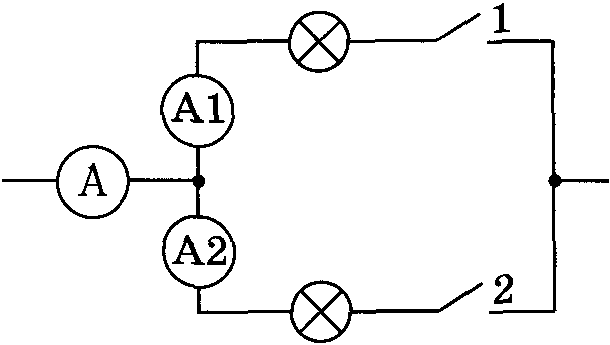
Дано: R1 = R2 = R; I = 3 А. I2 - ?
Решение
При замкнутых выключателях получаем схему
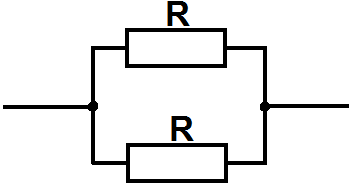
Сопротивление при параллельном соединении
![]()
![]()
![]()
Напряжение в цепи
U = IRэкв
![]()
При разомкнутом 1-м выключателе получаем схему
![]()
![]()
Ответ: I = 1,5 А.
Задача № 1388 [6].
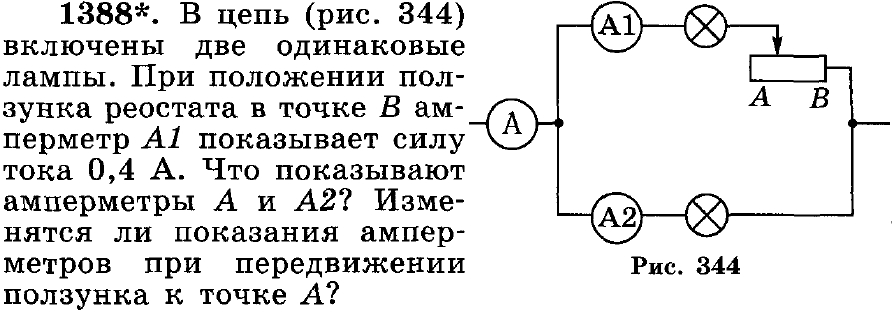
Дано: в точке B: R1 = R2 = R; I1 = 0,4 A. I, I2 - ?
Решение
При положении реостата в точке B его сопротивление равно нулю. Следовательно сопротивления параллельных ветвей одинаковые и силы тока равны
I2 = I1 = 0,4 A.
Сила тока в цепи
I = I1 + I2 = 0,4 A + 0,4 A = 0,8 A.
При перемещении ползунка реостата к точке A возрастает сопротивление 1-й ветви, поэтому напряжение в цепи, определяемое формулой
U = I1R1
также возрастает при неизменной силе тока I1.
Сила тока во 2-й цепи, определяемая формулой
![]() ,
,
также возрастает при неизменном сопротивлении R2.
Сила тока в цепи, определяемая формулой
I = I1 + I2,
также возрастает при неизменной силе тока I1.
Ответ: в точке B: I = 0,8 A, I2 = 0,4 A. При передвижении ползунка реостата к точке A силы тока I и I2 возрастают.
Задача № 1390 [6].

Дано: в точке B: R1 = 30 Ом; R2 = 60 Ом; R3 = 40 Ом. Rэкв - ?
Решение
Выделим часть схемы, сопротивление которой необходимо определить
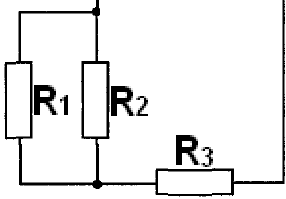
Эквивалентное сопротивление параллельно соединенных резисторов выразим из формулы
![]()
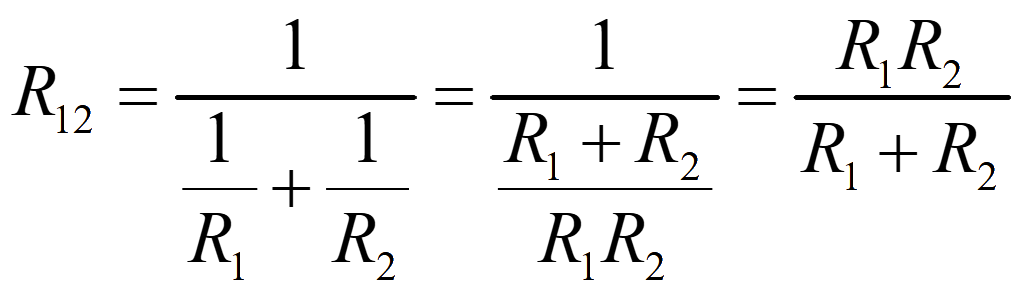
Получаем эквивалентною заданной схему с последовательным соединением сопротивлений
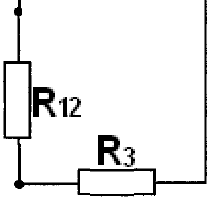
Эквивалентное сопротивление при последовательном соединении
![]()
![]()
Ответ: Rэкв = 60 Ом.
Напряжение источника тока без нагрузки равно ЭДС источника тока:
U = ε
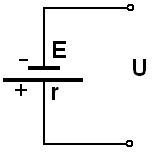
Другое изображение источника тока
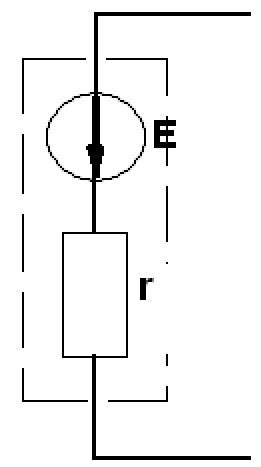
В замкнутой цепи ток направлен от положительной (длинной на схеме) клеммы батареи к отрицательной
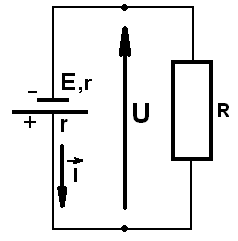 та
же схема
та
же схема
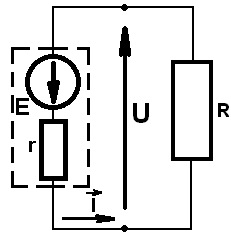
ЭДС источника тока в замкнутой полной цепи (закон Ома для замкнутой полной цепи):
ε = I(R+r),
где I – сила тока в замкнутой полной цепи, А;
R – внешнее сопротивление (сопротивление нагрузки), Ом;
r – внутреннее сопротивление источника тока, Ом;
ε - ЭДС источника тока, В.
Закон Ома для замкнутой полной цепи
![]()
Положительное направление тока источника от плюса к минусу во внешней цепи, а внутри источника тока от минуса к плюсу. Поэтому стрелка в окружности, изображающей ЭДС в цепи, направлена в сторону положительного направления тока во внешней цепи. Направление стрелки напряжения от большего потенциала к меньшему потенциалу, то есть также по направлению тока в цепи.
IR + Ir = ε.
Произведение тока на сопротивление называется падением напряжения на сопротивлении:
U = IR.
U + Ir = ε.
Внешнее сопротивление подключено к выводам источника тока, поэтому падение напряжения на внешнем сопротивлении равно напряжению на выходе источника тока, которое равно ЭДС минус падение напряжения на сопротивлении источника тока
U = ε – Ir.
Опыт короткого замыкания (замыкание выводов источника тока):
ε = Ir,
где I – сила тока в цепи источника тока при коротком замыкании, А;
r – внутреннее сопротивление источника тока, Ом.
В замкнутом участке электрической цепи может быть несколько последовательных источников тока. Выбирается произвольное направление обхода контура (цепи). Если ЭДС источника создает ток в направлении обхода контура, то эта ЭДС берется со знаком плюс. Если ЭДС источника пытается заставить течь ток в направлении, обратном обходу контура, то эта ЭДС берется со знаком минус.
![]() ,
,
где Σ — сумма.
В замкнутом участке электрической цепи при наличии нескольких источников тока направление силы тока не определено, поэтому выбирается произвольное направление тока. Если выбранное направление тока совпадает с направлением обхода контура (цепи), то сила тока берется со знаком плюс, в противном случае со знаком минус.
Сопротивление источников тока r равно сумме сопротивлений отдельных источников тока.
![]()
В замкнутой электрической цепи может быть несколько последовательно соединенных внешних сопротивлений. Общее сопротивление равно сумме отдельных сопротивлений:
![]()
Закон Ома для замкнутой цепи можно записать в виде второго закон Кирхгофа:
![]()
Если направление тока или ЭДС совпадает с направлением обхода контура, то они берутся со знаком «+». В сложной электрической цепи рассматривается несколько замкнутых контуров с током, для каждого из которых составляются уравнения по второму закону Кирхгофа. Каждый последующий контур, для которого составляются уравнения по второму закону Кирхгофа должен содержать новую ветвь.
Определяем число узлов (мест разветвления цепи) и ветвей цепи (участков цепи между двумя узлами). Произвольным образом нумеруем показываем направления токов в ветвях. Выбираем произвольное направление обхода замкнутых контуров в цепи (обычно по часовой стрелке).
Первый закон Кирхгофа
Количество зарядов, притекающих к узлу, равно количеству зарядов, утекающих от узла. Если принять за положительные токи, направленные к узлу, то отрицательными будут токи, направленные от узла. Сумма токов в ветвях, имеющих общий узел равна нулю:
![]() ,
,
где b – количество ветвей, исходящих из узла;
i – какая-то ветвь;
Ii – ток в этой ветви, взятый со своим знаком.
По первому закону Кирхгофа составляется количество уравнений на одно меньше, чем число узлов в цепи. По второму закону Кирхгофа составляется число уравнений равное разнице между числом неизвестных токов в ветвях и числом составленных по первому закону Кирхгофа уравнений. Из уравнений по первому и второму законам Кирхгофа составляется система, число уравнений которой равно числу ветвей цепи (числу неизвестных токов). Решение системы дает искомые токи в ветвях. Если ток получился с отрицательным знаком, то фактическое направление тока противоположно произвольно выбранному.
![]()
Если при решении уравнения
![]()
значение тока получается со знаком минус, то фактически ток в цепи протекает в направлении обратном выбранному направлению тока.
Сумма падений напряжений на внешних и внутренних сопротивлениях равна сумме ЭДС источников тока:
![]() .
.
![]()
Мощность
![]() .
.
![]()
Работа по перемещению зарядов по проводнику с током
![]() .
.
![]()
![]()
![]()
Задача [11 (Открытый банк заданий ГИА-9 2014 г. fipi.ru)]. Найдите силу тяги, развиваемую при скорости 12 м/с электровозом, работающим при напряжении 3 кВ и потребляющим ток 1,6 кА. КПД двигателя электровоза равен 85%.
Дано: υ = 12 м/с; U = 3000 В; I = 1600 А; КПД = 85 %. F - ?
Решение
Мощность, Вт
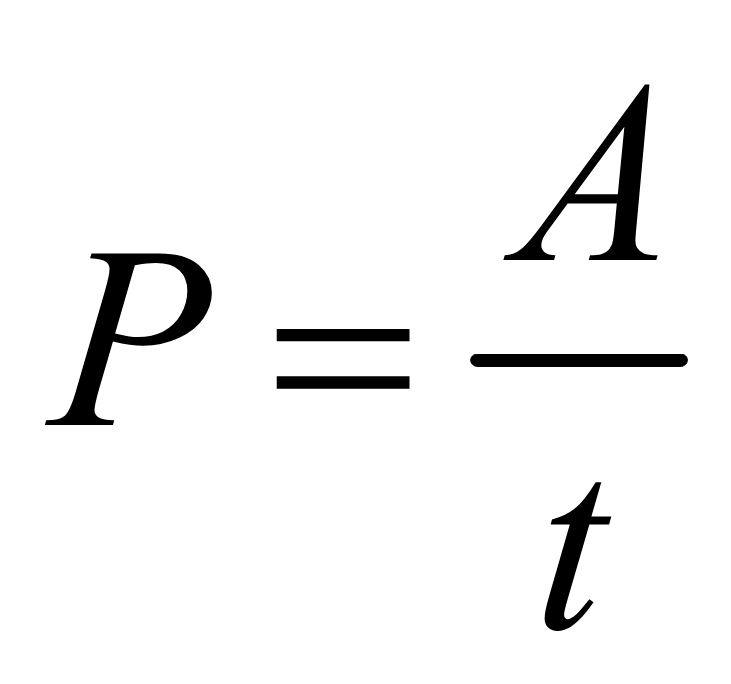
Механическая работа, Дж
A = Fs
Подставляем в формулу, определяющую мощность
![]()
КПД двигателя
![]() ,
,
где Aполезная - полезная работа, Дж;
Aзатраченная - затраченная работа, Дж.
Числитель и знаменатель помножим и поделим на время
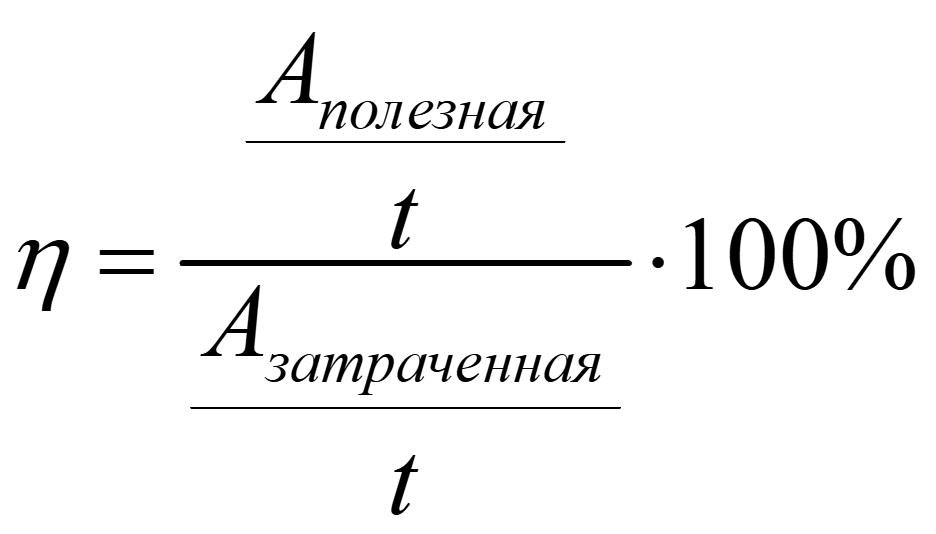
![]() ,
,
где Pполезная - полезная мощность, Дж;
Pзатраченная - затраченная мощность, Дж.
Мощность, подводимая из контактной сети
Pзатраченная = UI
Подставляем
![]()
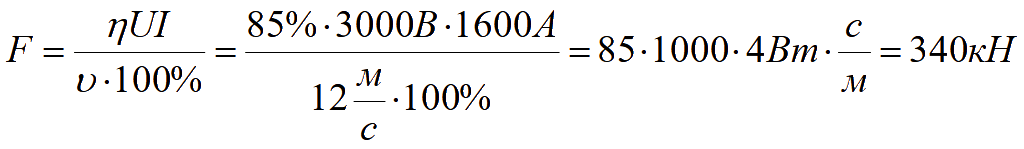
Ответ: F = 340 кН.
Задача № 27 [10 (Демо ГИА 2014)]. Сколько времени потребуется электрическому нагревателю, чтобы довести до кипения 2,2 кг воды, начальная температура которой 10 0С? Сила тока в нагревателе 7 А, напряжение в сети 220 В, КПД нагревателя равен 45%.
Решение
1 способ
КПД нагревателя
![]() ,
,
где Aполезная - полезная работа, Дж;
Aзатраченная - затраченная работа, Дж.
Полезная работа нагревателя расходуется на нагрев воды
Aполезная = Q = cm(t2 – t1)
где c – удельная теплоемкость воды, c = 4200 Дж/(кг0С);
m – масса воды, кг;
t2 – t1) конечная температура, 0С;
(t2 – t1) — начальная температура, 0С.
Мощность электрического тока
N = UI;
![]() ,
,
где t – время, с.
Отсюда
![]()
![]()
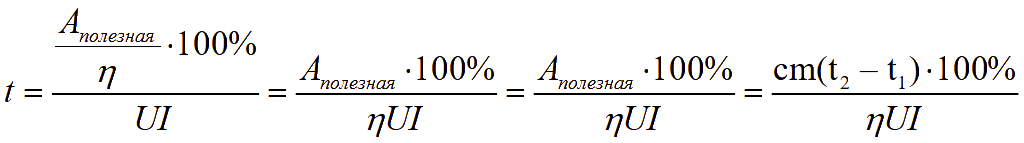
![]()
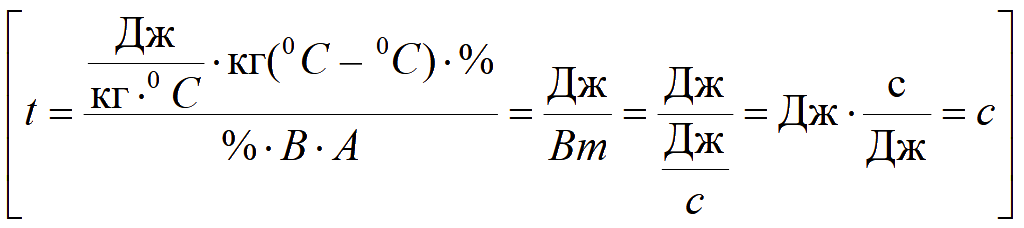
2 способ
![]()
![]()
![]()
![]()
![]()
![]()
Теплоемкость воды c = 4200 Дж/(кг · 0C)
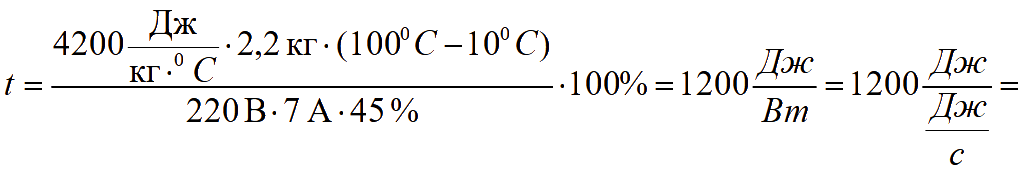
= 1200 с = 20 минут.
Ответ: t = 1200 c = 20 минут.
Работа по перемещению зарядов по проводнику с током равна энергии, которая выделяется в виде тепла
![]() .
.
Обычно при расчете теплоты, выделившейся при прохождении тока через нагревательный элемент используется закон Джоуля-Ленца, описываемый формулой
![]()
Сила Ампера
![]() ,
,
где B – магнитная индукция, Тл;
I – сила тока, А;
∆ℓ – длина проводника, м;
![]() - угол между вектором
магнитной индукции и силой тока, градусы или радианы.
- угол между вектором
магнитной индукции и силой тока, градусы или радианы.
© 05.02.2021 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru