© 2023 Ольшевский Андрей Георгиевич репетитор по математике, информатике, физике, программированию, авиации, двигателям, электронике, искусственному интеллекту, техническим дисциплинам по Скайп da.irk.ru

Сайт super-code.ru с полезными темами, которые вы можете сохранить бесплатно

Матрицы, способы решения задач, формулы

1 Матрицы

Матрица - это таблица значений (чисел, выражений, букв), заключенных в фигурные скобки (матрица), [матрица], {матрица}, <матрица>, ||матрица||.

Если матрица содержит одну строку, то она называется вектор-строка или строковой матрицей, или матрицей-строкой. Например, вектор-строка, содержащая координаты вектора в пространстве

(x y z).

Если матрица содержит один столбец, то она называется вектор-столбец или столбцовой матрицей, или матрицей-столбцом. Например, вектор-столбец, содержащий координаты вектора:

Нулевая матрица O состоит из элементов, которые все равны нулю

Матрица, содержащая m строк и n столбцов называется матрицей размера m на n. Элементы матрицы имеют индексы, первый из которых указывает на номер стоки, а второй - номер столбца. Применительно к матрицам всегда на первом месте строка, а на втором месте говорится столбец! Например, элемент первой строки первого столбца будет обозначаться a₁₁, элемент второй строки в третьем столбце обозначается a₂₃, элемент m-ной строки n-го столбца a_mn. Матрица 3 на 4 (можно записать 3 x 4) будет выглядеть так:

Матрица m на n (m x n)

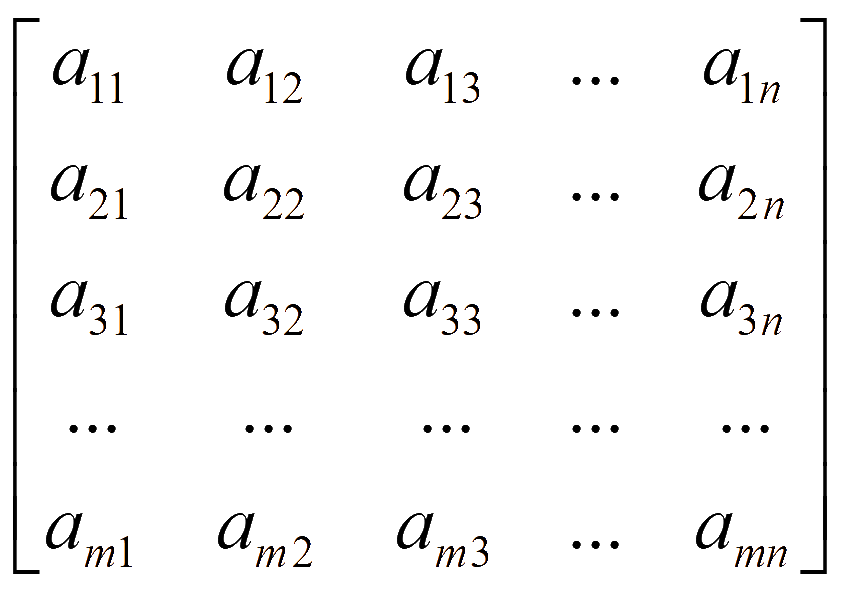
Матрицы называются равными, если они содержат равное число строк и столбцов, а также равны их соответствующие элементы.

Квадратная матрица содержит одинаковое число строк и столбцов и называется квадратной матрицей m x m. Число строк m называется порядком квадратной матрицы.

Элементы квадратной матрицы a₁₁, a₂₂, …, a_mm образуют главную диагональ, а вторую диагональ образуют элементы a_1m, a_2m-1, …, a_m1.

Квадратная матрица называется симметрической, если равны ее элементы, симметричные относительно главной диагонали.

Квадратная матрица называется диагональной, если все ее элементы, не принадлежащие главной диагонали равны нулю

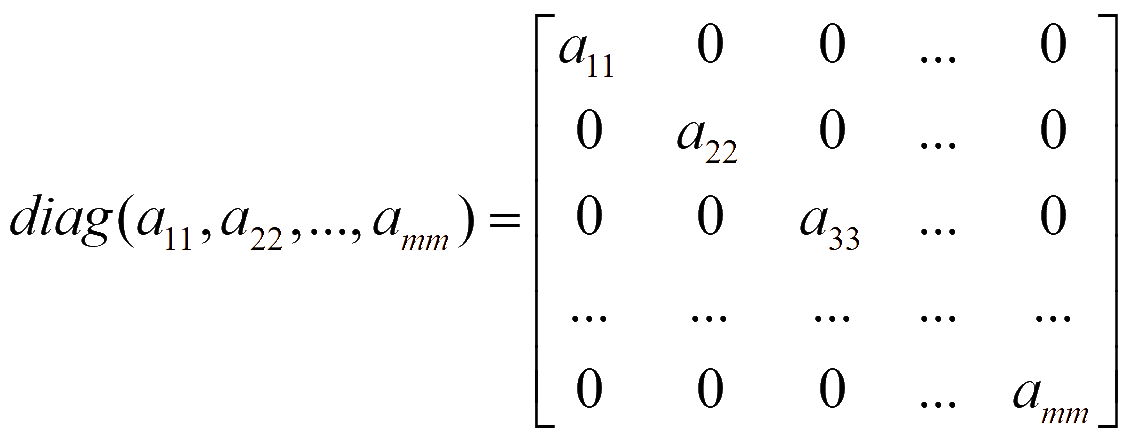
Единичная матрица E — это диагональная матрица с элементами на главной диагонали равными 1

Треугольная квадратная матрица содержит нулевые элементы по одну сторону от главной диагонали. Соответственно верхняя и нижняя треугольные матрицы:

2 Алгебра матриц

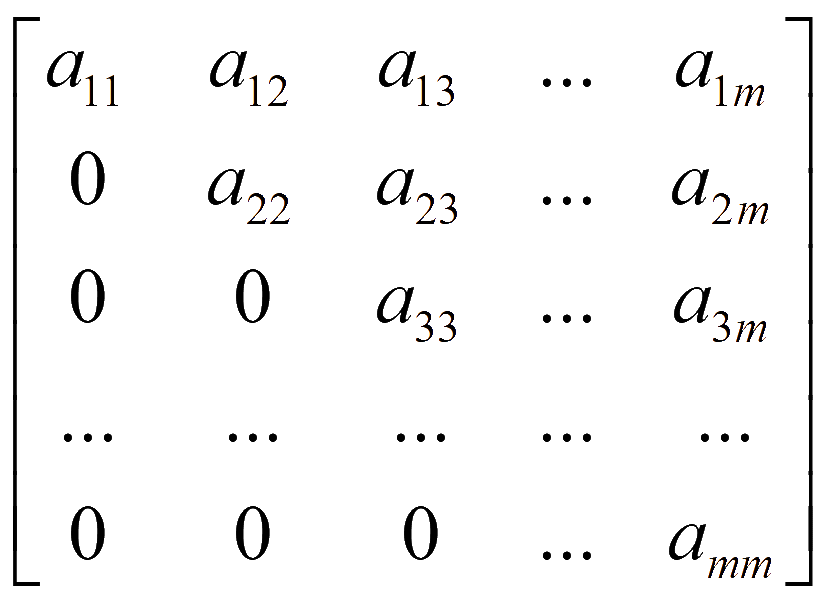
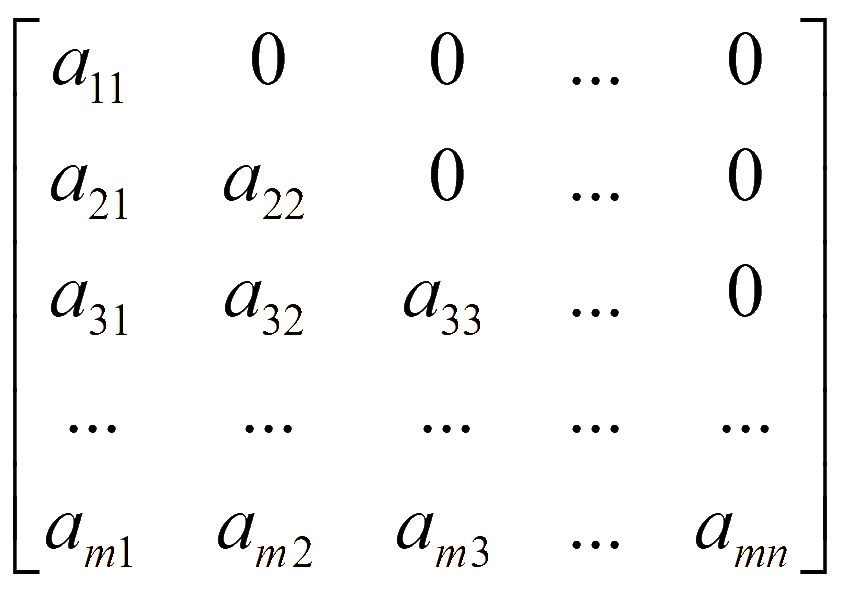
При умножении матрицы A размера m на n на коэффициент k происходит умножение на коэффициент k каждого элемента этой матрицы. Например, матрица 2 на 2

kA = k =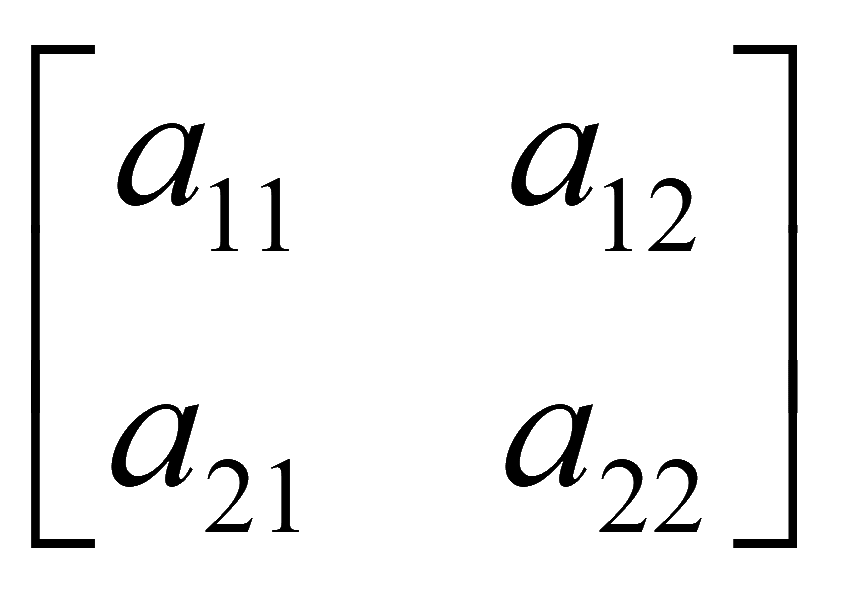

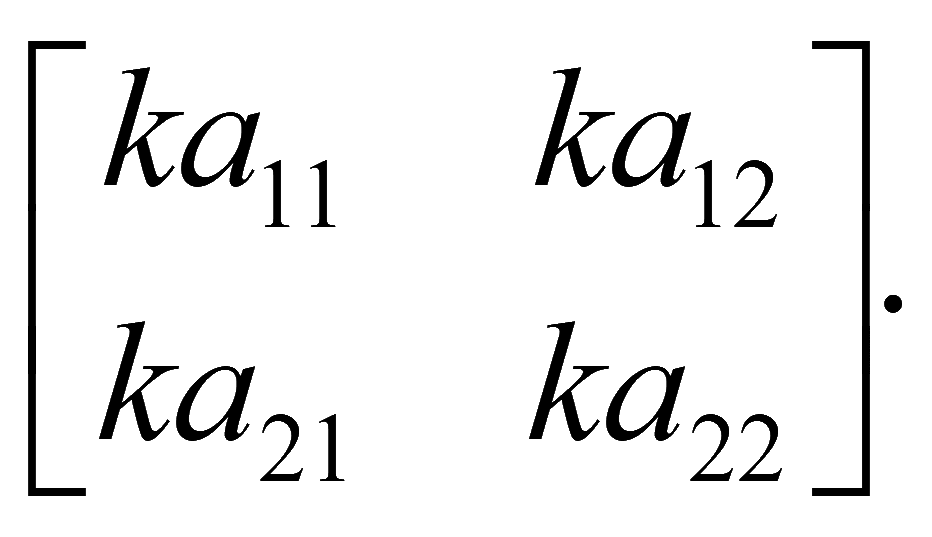
За знак матрицы можно выносить общий множитель всех элементов матрицы.

Свойства умножения матрицы на число:

1) kА = Аk;

2) (kb)А = k(bА) = b(kА), где k, b ∈ R;

3) (kА)^Т = kА^Т;

4) 0ּА = 0.

При сложении матриц размера m на n происходит сложение соответствующих элементов. Например, матрицы 2 на 2

A + B = + =

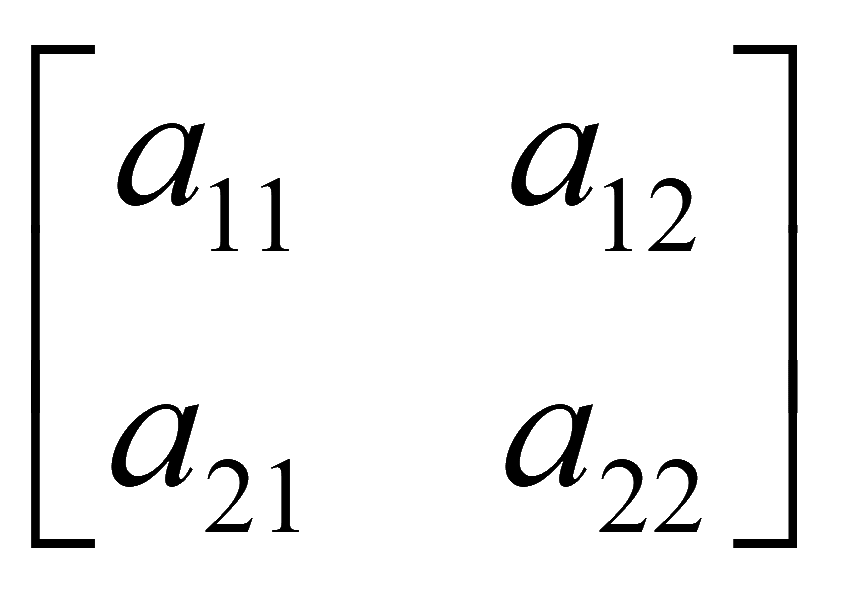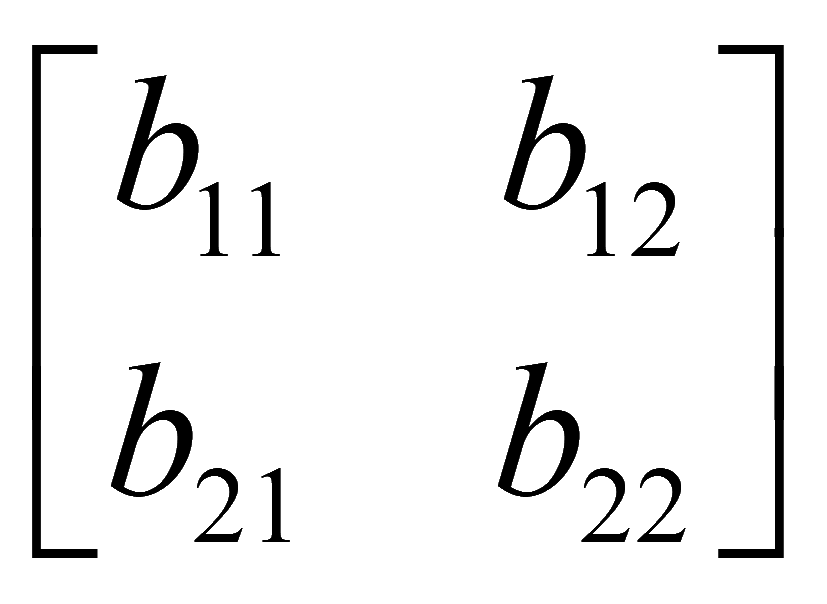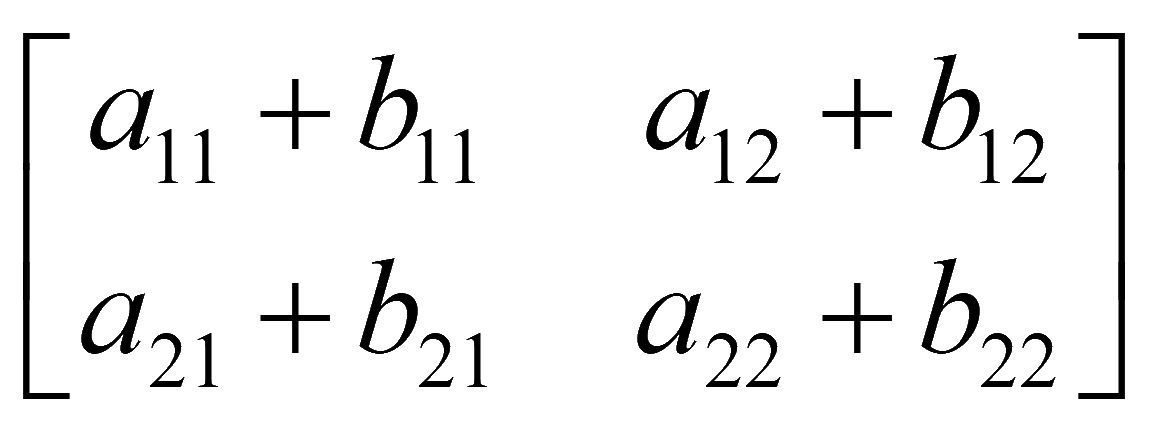
При вычитании матриц размера m на n происходит вычитание соответствующих элементов. Например, матрицы 2 на 2

A - B = - =

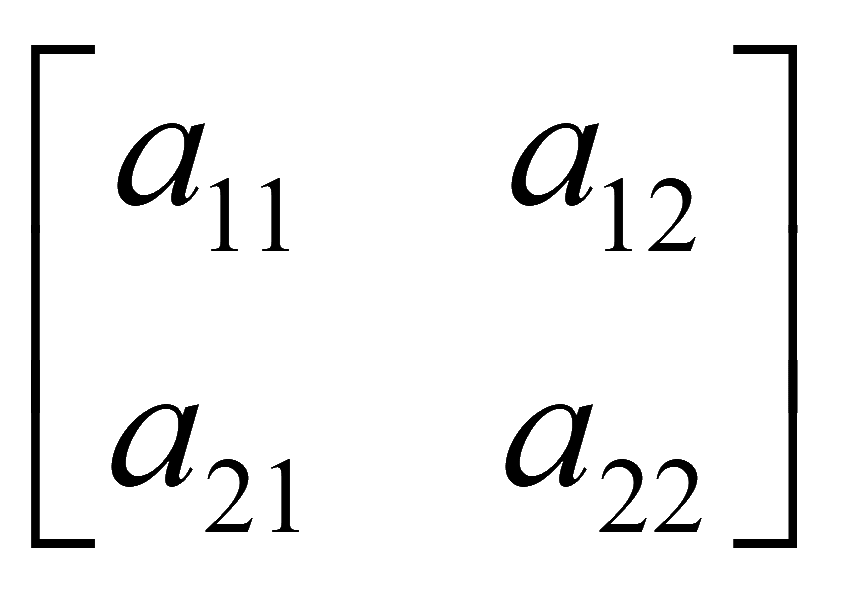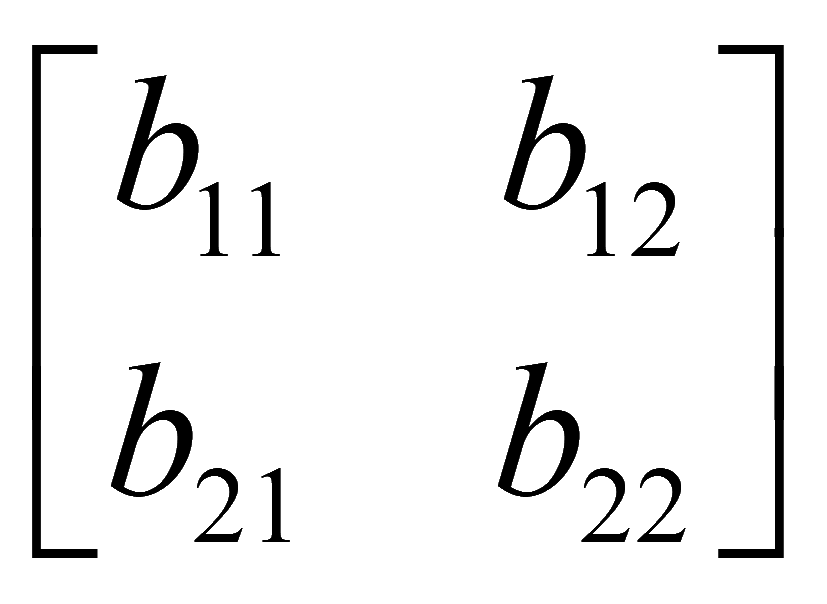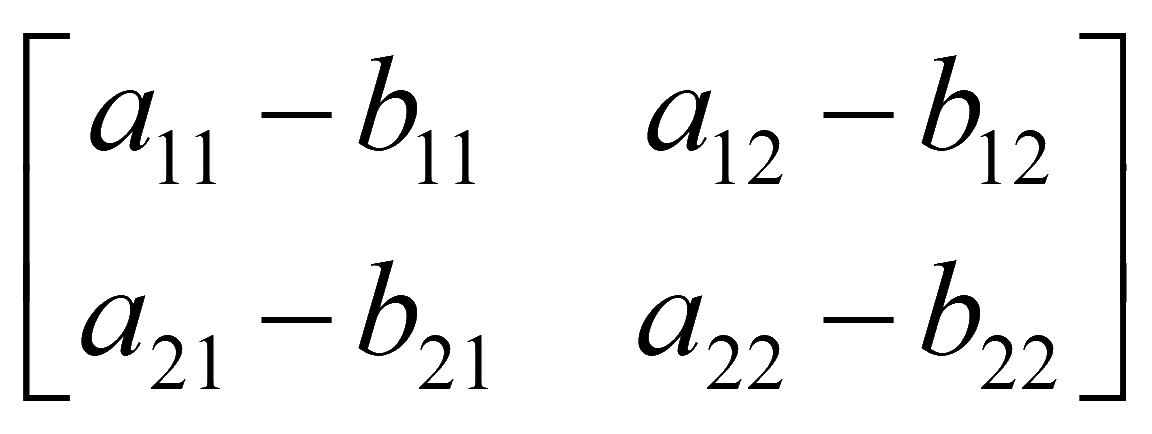
Свойства суммы матриц:

1. коммутативность А + В = В + А;

2. ассоциативность (А + В) + С = А + (В + С);

3. дистрибутивность к умножению на число k ∈ R: k(А+В) = kА+kВ;

4. O + А = А, где O – нулевая матрица;

5. А + (–А) = O, где (–А) – матрица, противоположная матрице А;

6. (А + В)^Т = А^Т + В^Т.

При перемножении матриц производятся операции со строками 1-й матрицы и столбцами 2-й матрицы. На пересечении i-й строки 1-й матрицы с j-м столбцом 2-й матрицы получается ij-й элемент результирующей матрицы в результате перемножения элементов i-й строки 1-й матрицы на элементы j-го столбца 2-й матрицы:

c_ij = a_i1 · b_1j + a_i2 · b_2j + a_i3 · b_3j + a_i4 · b_4j + a_i5 · b_5j + … + a_in · b_nj.

При i = 1

c_1j = a₁₁ · b_1j + a₁₂ · b_2j + a₁₃ · b_3j + a₁₄ · b_4j + a₁₅ · b_5j + … + a_1n · b_nj.

При i = 1 и j = 1 получаем элемент на пересечении 1-й строки и 1-го столбца

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ + a₁₃ · b₃₁ + a₁₄ · b₄₁ + a₁₅ · b₅₁ + … + a_1n · b_n1.

Элементы 1-й строки 1-й матрицы, умножаются на элементы 1-го столбца 2-й матрицы и складываются с произведением последующих элементов 1-й строки 1-й матрицы на элементы 1-го столбца 2-й матрицы: первый элемент строки умножаем на первый элемент столбца, затем складываем с произведением второго элемента строки на второй элемент столбца и т. д. Поэтому число элементов в строке (число столбцов) первой матрицы должно быть равно числу элементов в столбце (числу строк) матрицы, на которую умножаем. При перемножении матриц на пересечении строки со столбцом получается соответствующий элемент результирующей матрицы.

Элементы матрицы С вычисляются следующим образом:

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁

c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂

c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁

c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂

A · B = · =

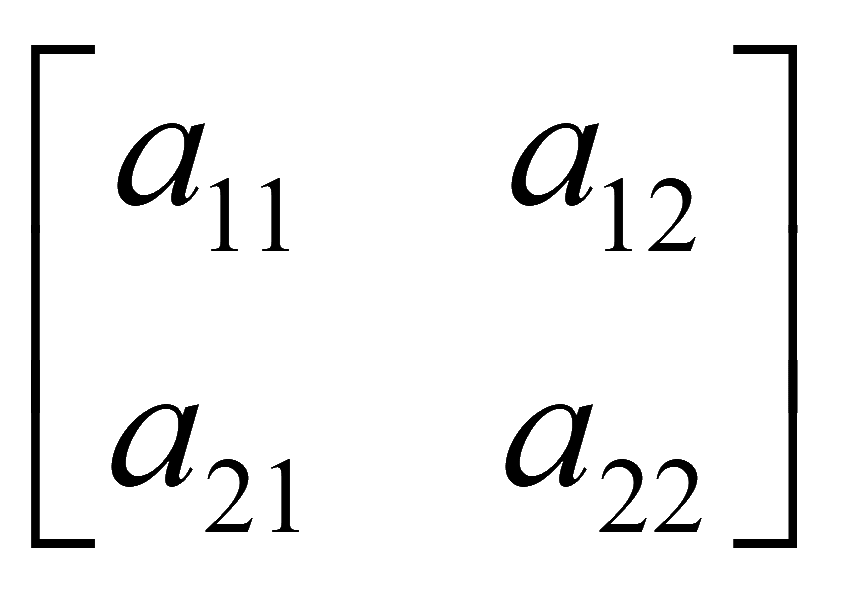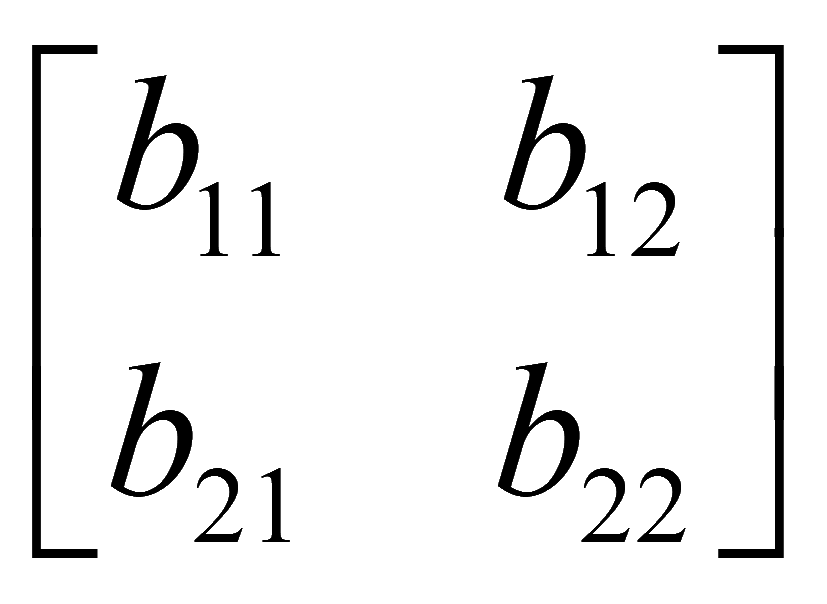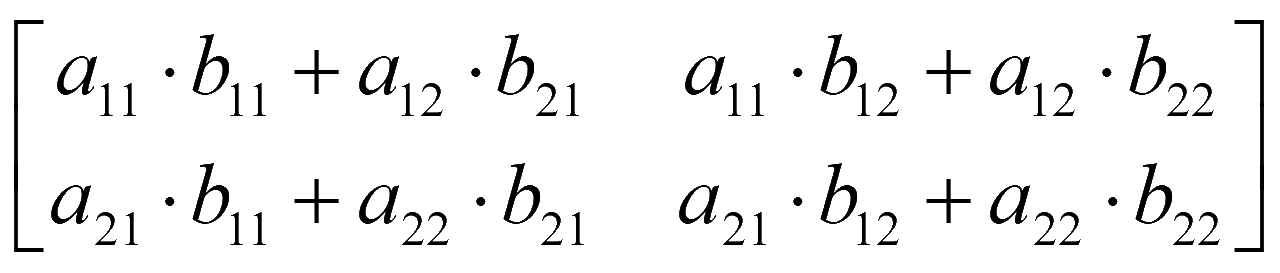
A² = A · A = · =

= =

=

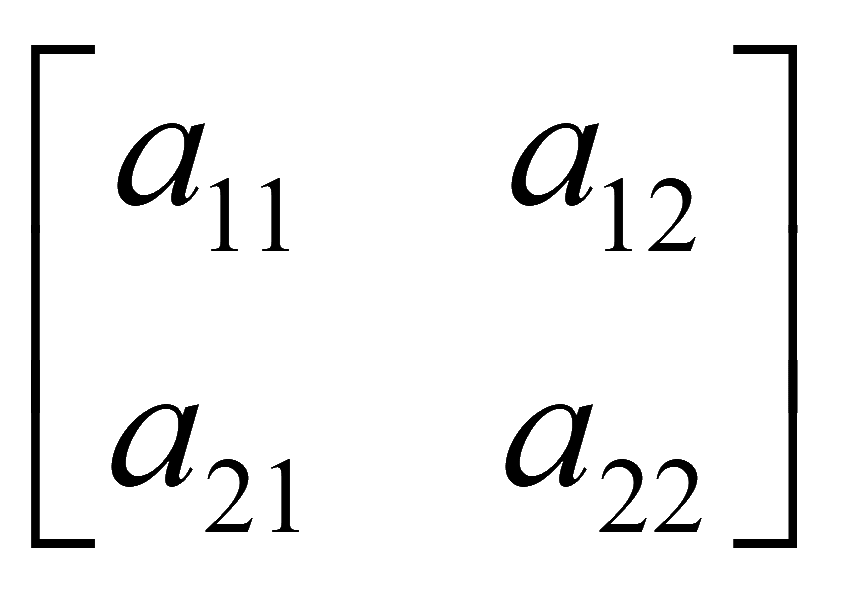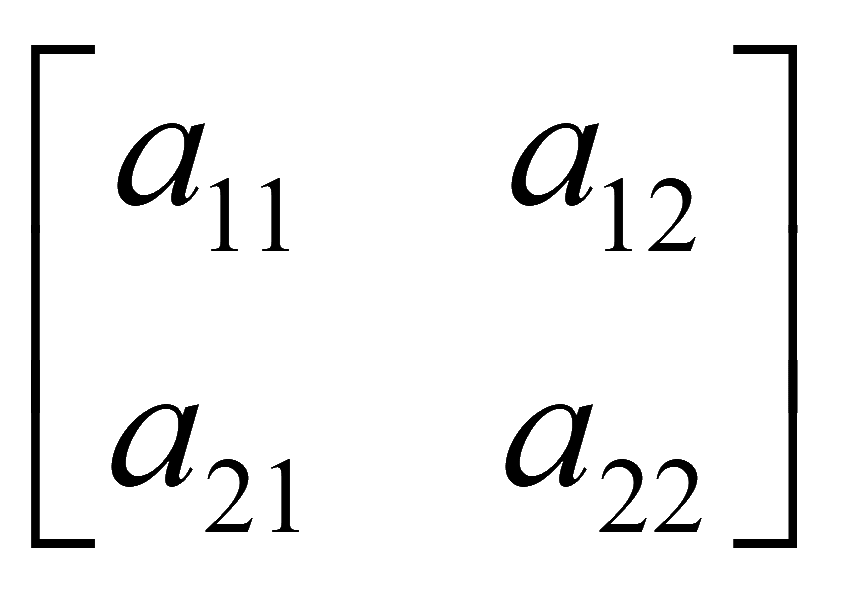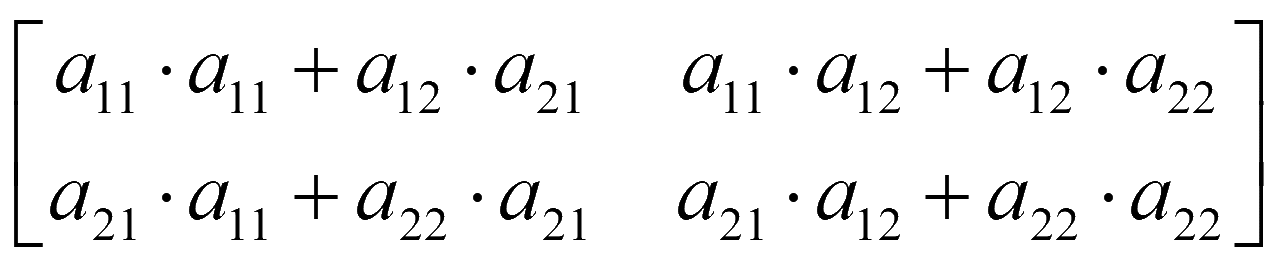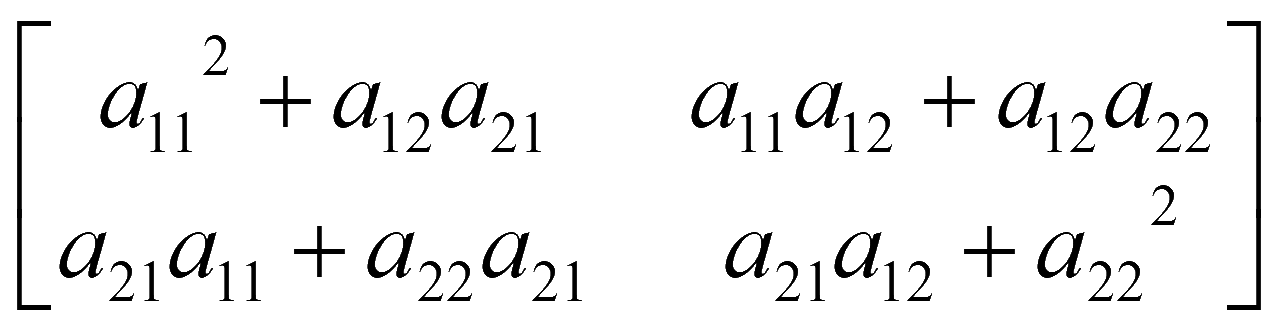
Свойства произведения матриц:

1) некоммутативность: АВ ≠ ВА, даже если А и В, и В и А согласованы. Если же АВ = ВА, то матрицы А и В называются коммутирующими (матрицы А и В в этом случае обязательно будут квадратными).

2) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.

3) A·O = O·A = O.

4) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.

5) ассоциативность АВС=А(ВС)=(АВ)С:

6) дистрибутивность относительно сложения:

(А + В)∙С = АС + ВС,

А∙(В + С) = АВ + АС.

7) (А∙В)^Т = В^Т∙А^Т, порядок перемножения при этом изменяется!

3 Определитель квадратной матрицы

Определитель существует лишь для квадратной матрицы. Определитель матрицы - это таблица значений (чисел, выражений, букв), заключенных в вертикальные линии |определитель матрицы|. Определитель матрицы A может записываться как |A|, Δ и как det A.

Для квадратной матрицы существует определитель. В этом случае таблица значений заключается в две вертикальные черты. Например определители второго порядка

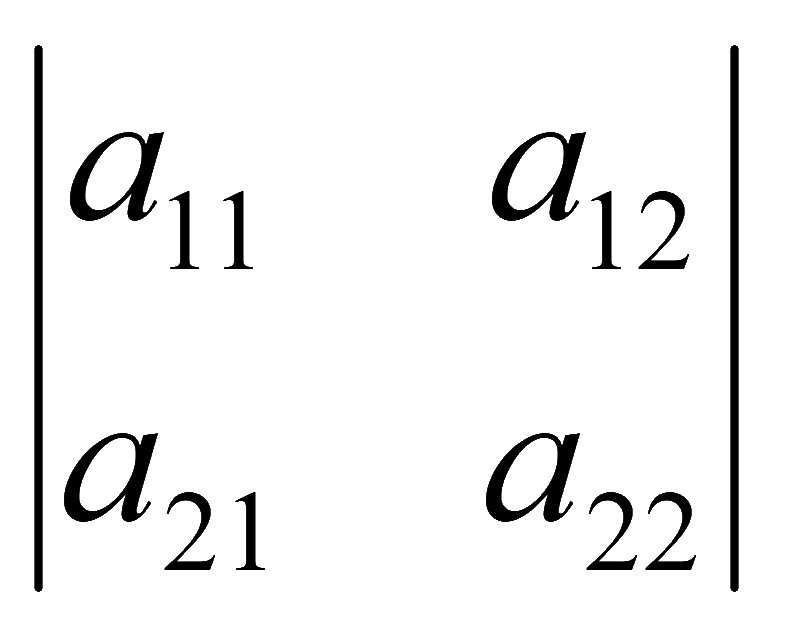
Определители третьего порядка

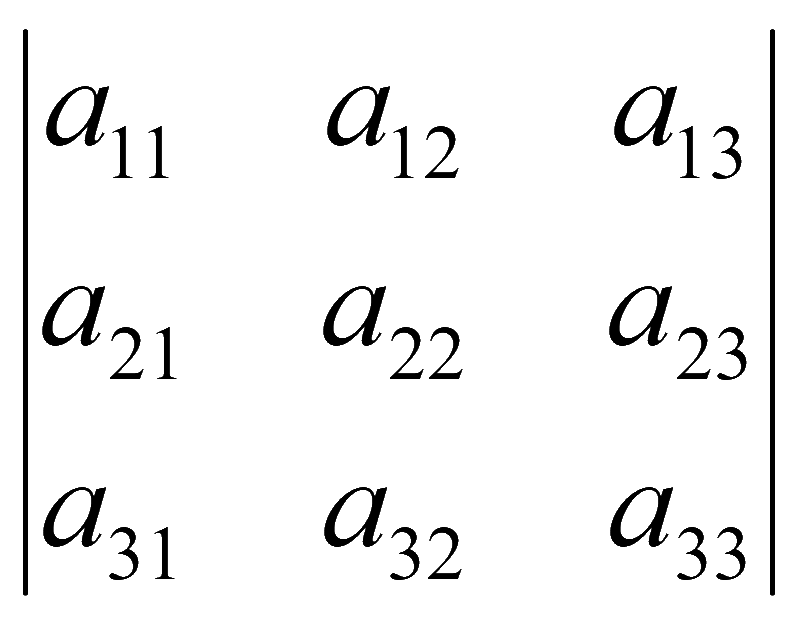
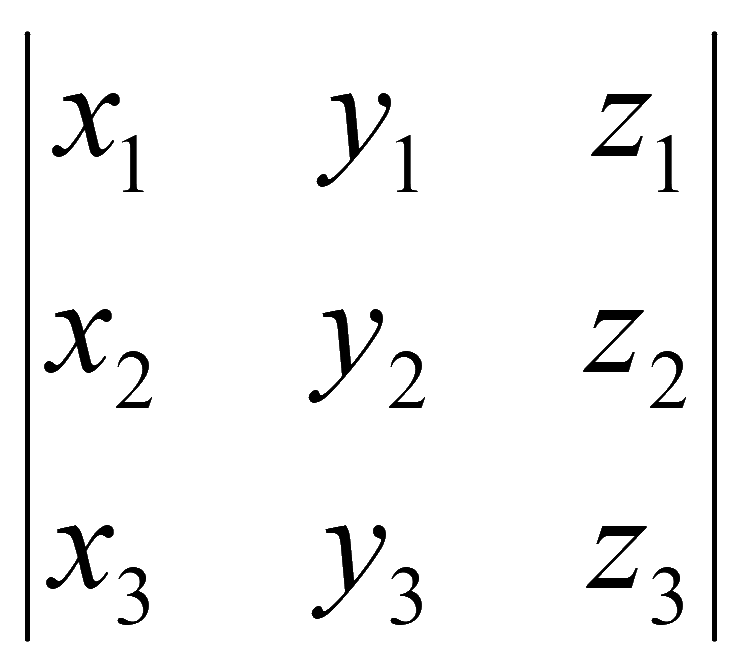
Для квадратной матрицы A

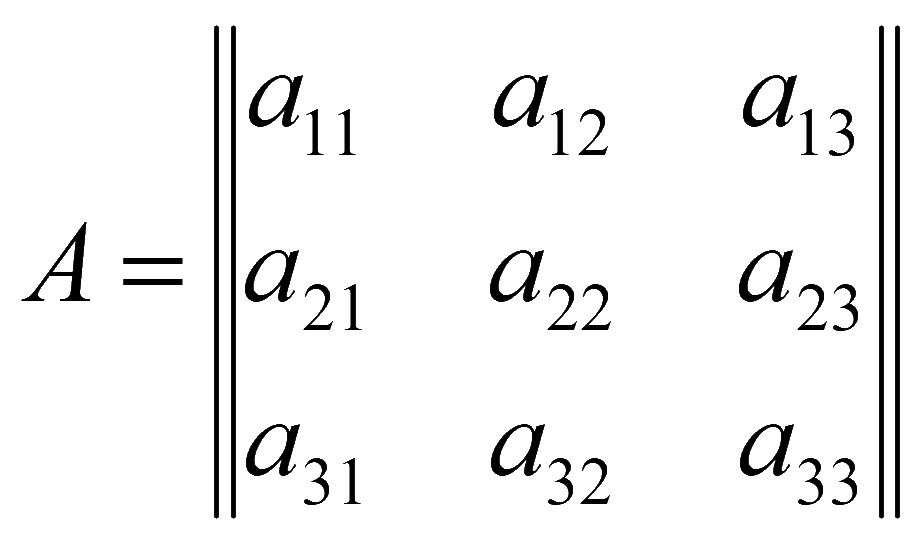
существует определитель

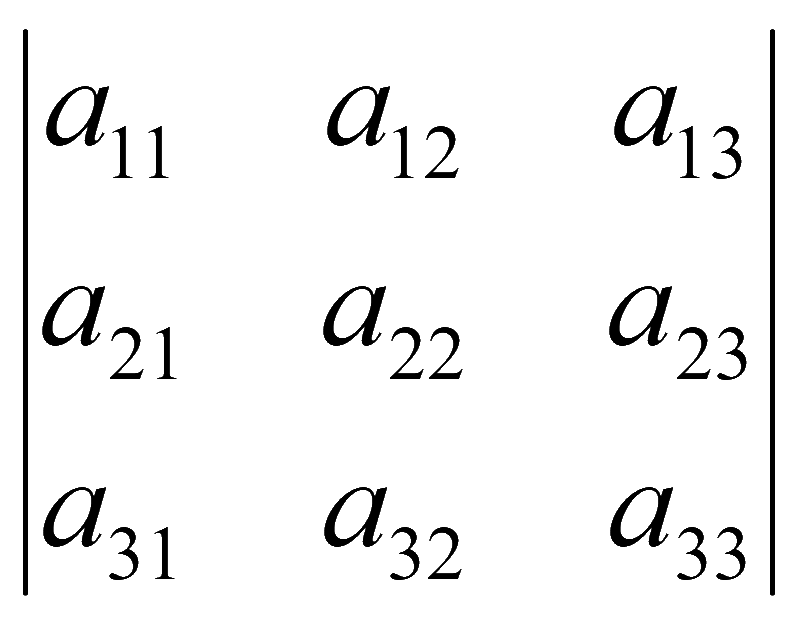
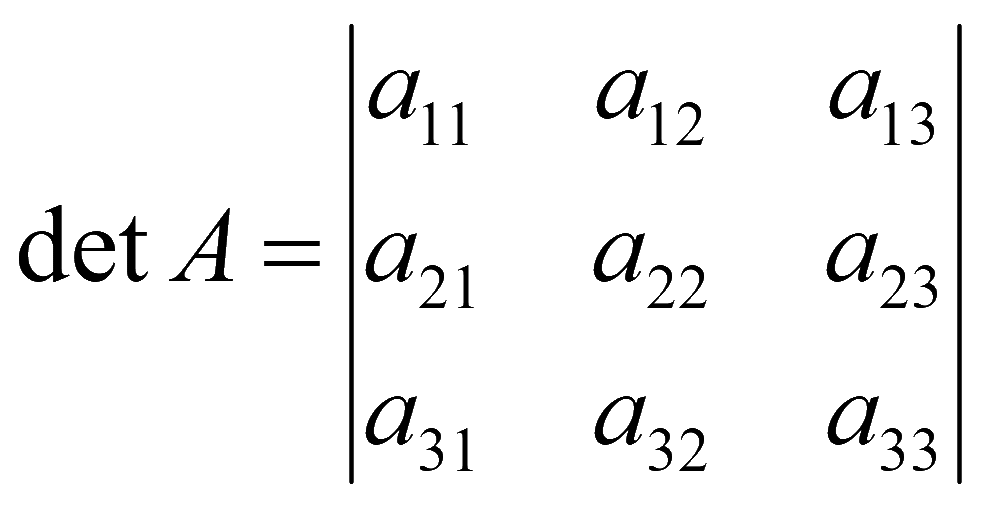
Пример. Найдем определитель для матрицы 2 на 2

A =

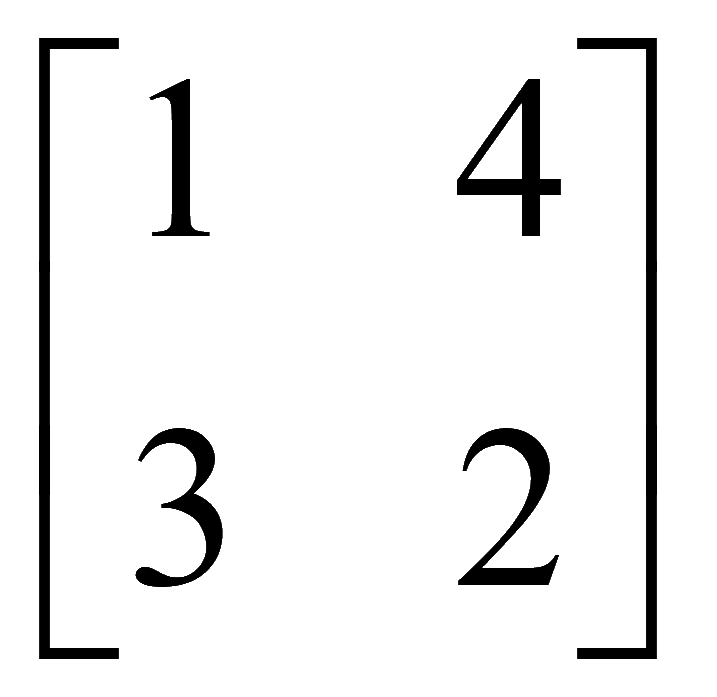
Определитель матрицы

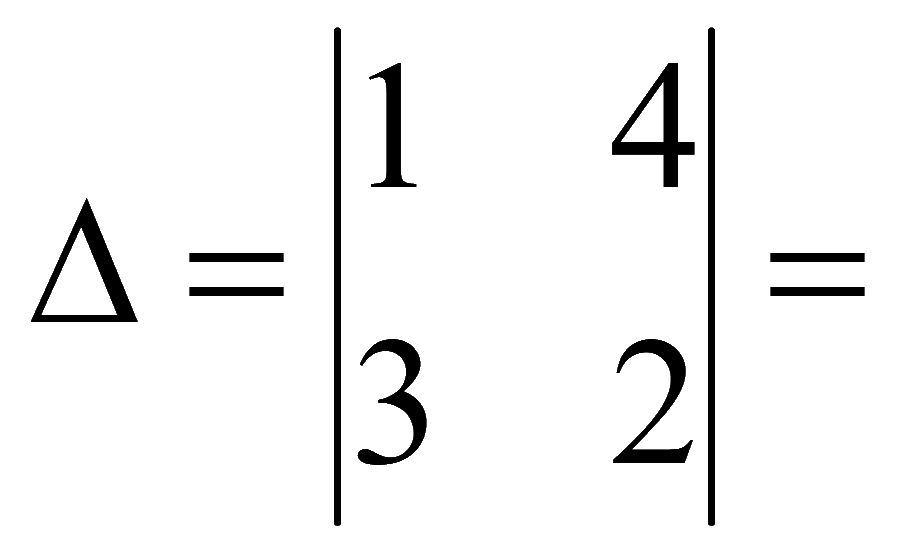
= 1·2 - 4·3 = -10

4 Транспонированная матрица

Если строки матрицы A поменять местами со столбцами, то получится транспонированная матрица A^Т. Для этого 1-ю строку помещаем в 1-й столбец, 2-ю строку помещаем в 2-й столбец и т. д. Если матрица A размера m на n, то транспонированная матрица A^Т будет размера n на m.

Например, дана матрица 2 на 2

A =

транспонированная матрица

A^Т =

5 Алгебраическое дополнение элемента матрицы

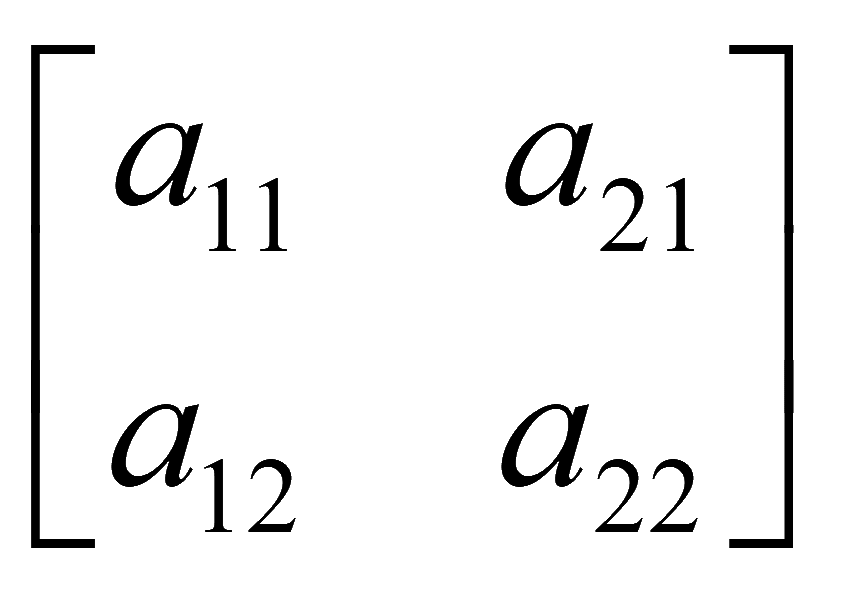
Алгебраическое дополнение элемента a_ij матрицы:

A_ij = (-1)^i+jM_ij,

где i – номер строки;

j – номер столбца;

M_ij – минор элемента a_ij, представляющий из себя определитель элементов матрицы, оставшихся после вычеркивания i – той строки и j – того столбца.

(-1) в четной степени равен 1. (-1) в нечетной степени равен -1.

Для квадратной матрицы 3 на 3

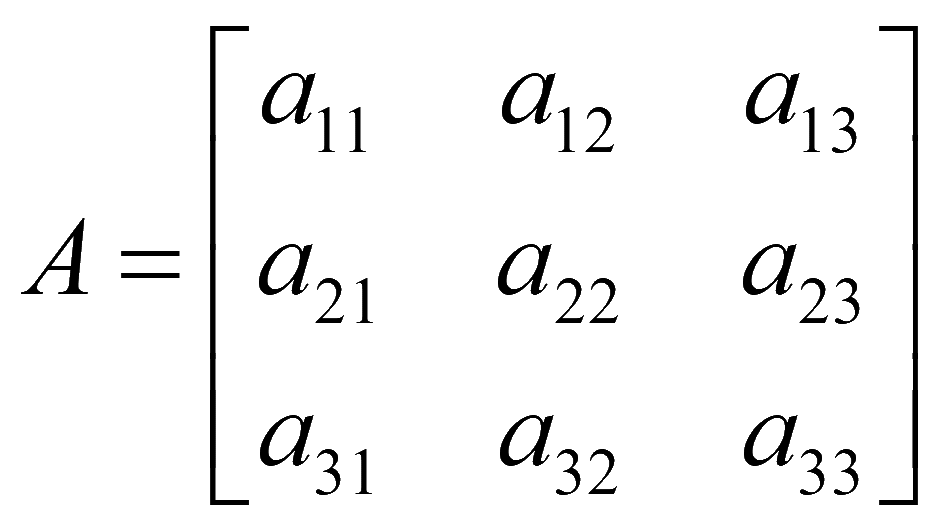
определим алгебраические дополнения элементов этой матрицы A.

Алгебраическое дополнение элемента a₁₁ матрицы A:

A₁₁ = (-1)¹⁺¹M₁₁ = (-1)²·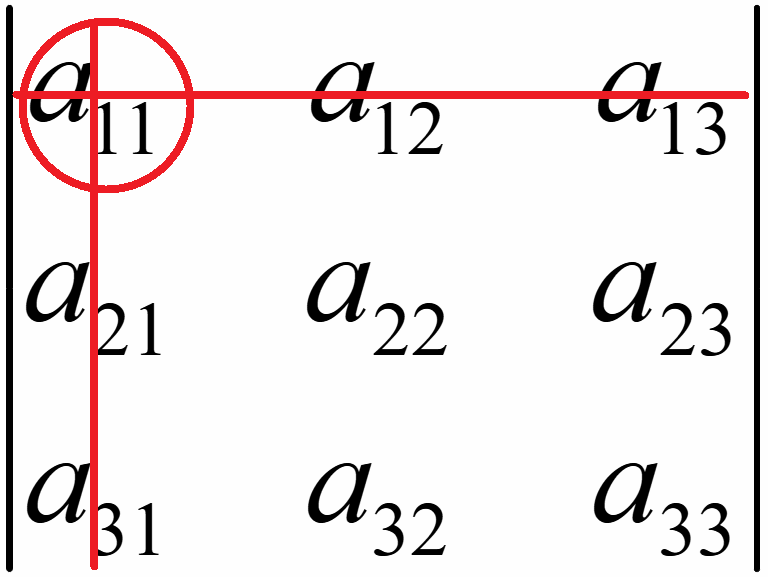 = 1·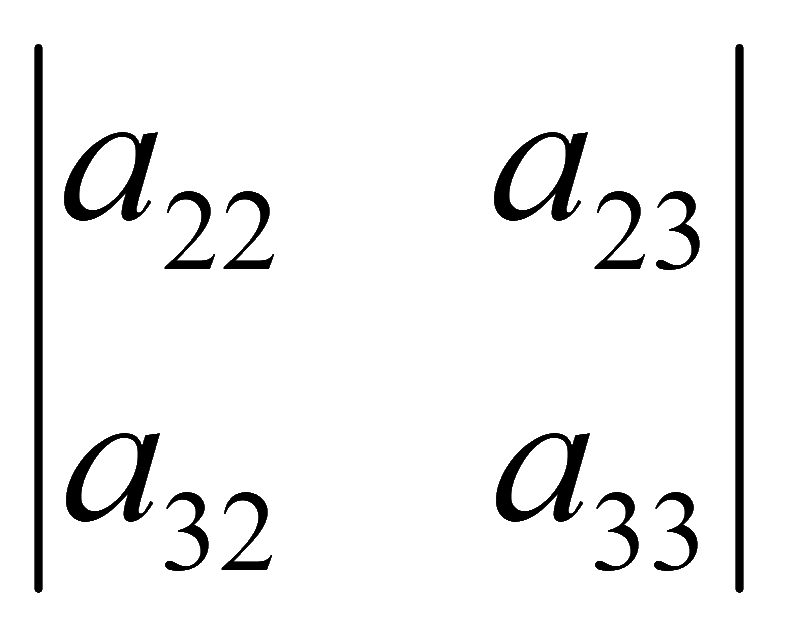 = a₂₂a₃₃ — a₂₃a₃₂.

Алгебраическое дополнение элемента a₁₂ матрицы A:

A₁₂ = (-1)¹⁺²M₁₂ = (-1)³·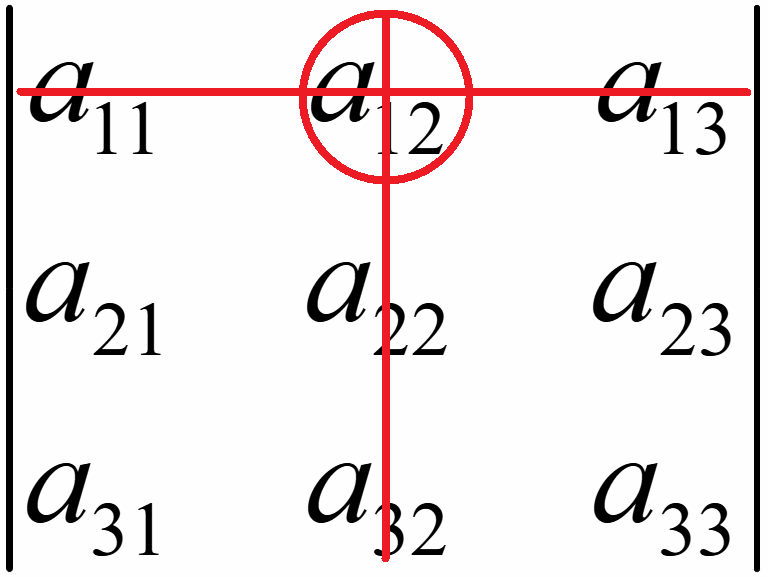 = -1·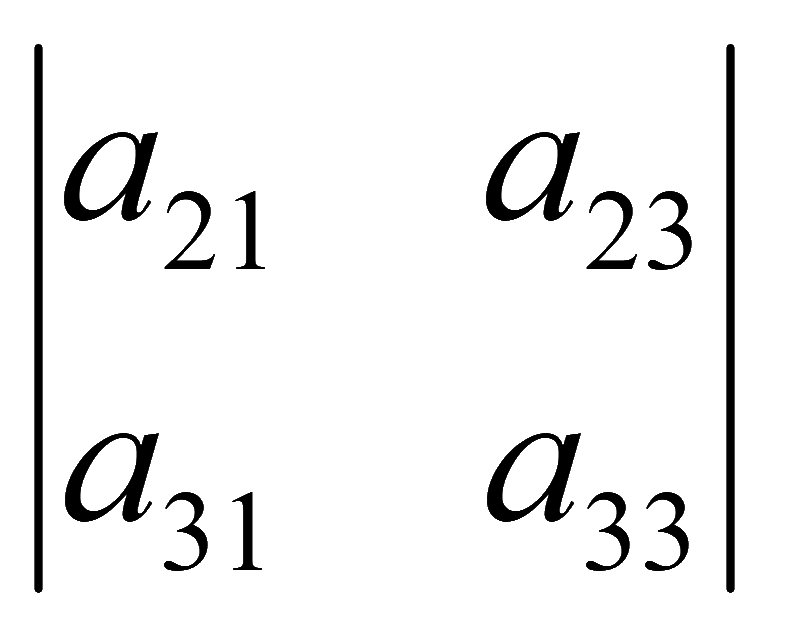 = -(a₂₁a₃₃ — a₂₃a₃₁).

…

Алгебраическое дополнение элемента a₃₃ матрицы A:

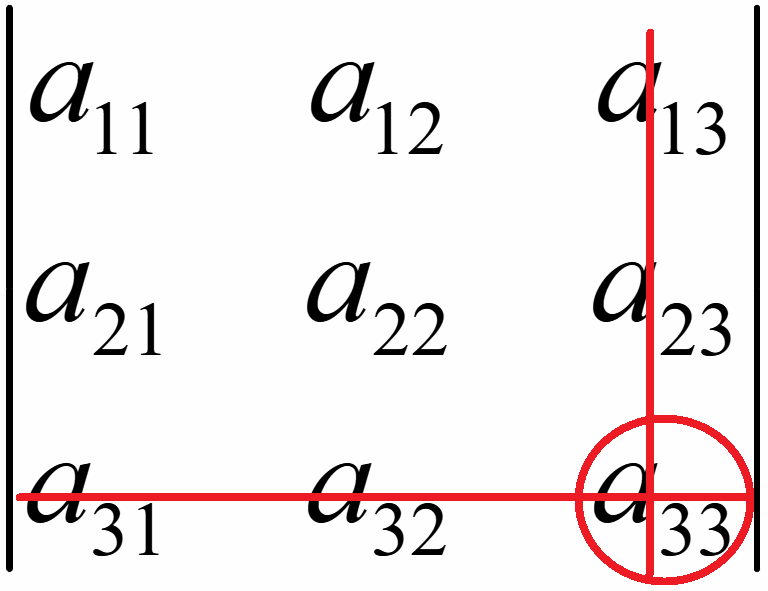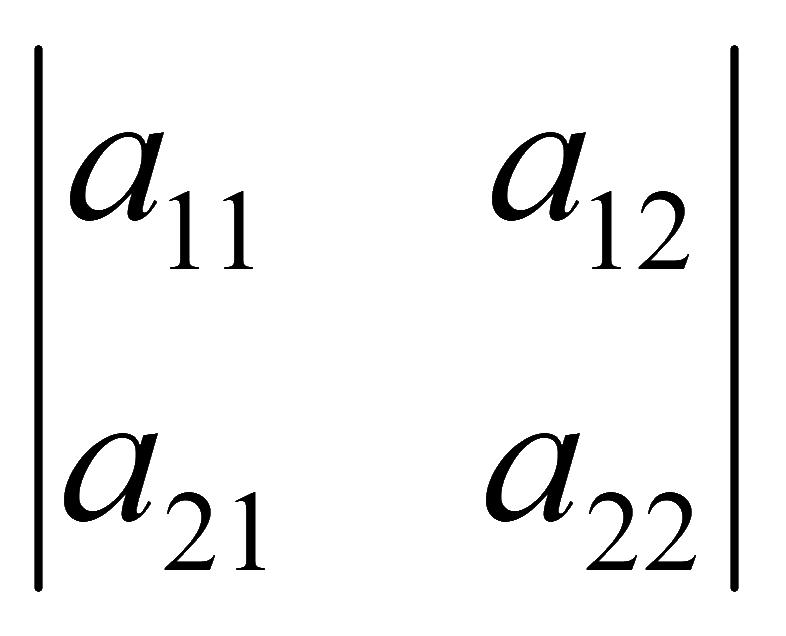A₃₃ = (-1)³⁺³M₃₃ = (-1)⁶ = 1· = a₁₁a₂₂ - a₁₂a₂₁.

6 Союзная матрица составляется из алгебраических дополнений

- союзная матрица, составленная из алгебраических дополнений элементов матрицы A, которые транспонируются.

Для квадратной матрицы 3 на 3

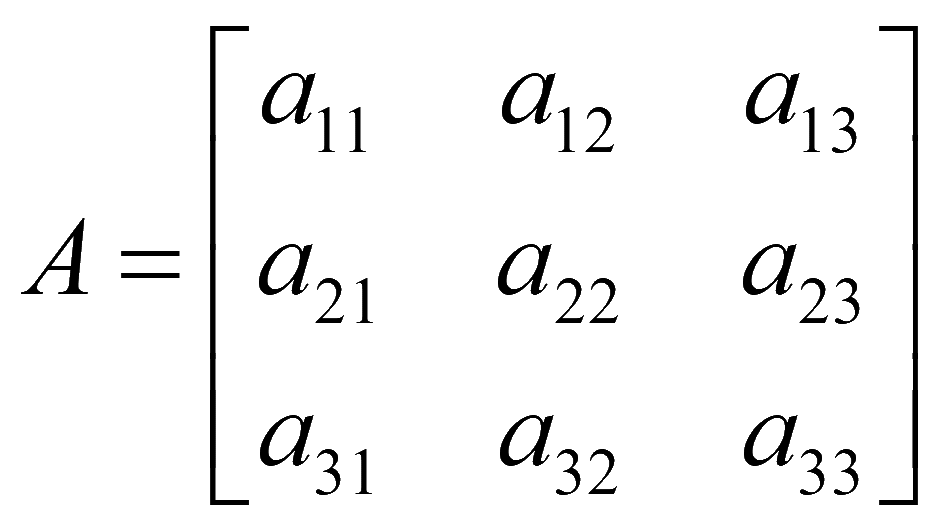
союзная матрица также будет 3 на 3, но элементами являются алгебраические дополнения

7 Свойства определителей

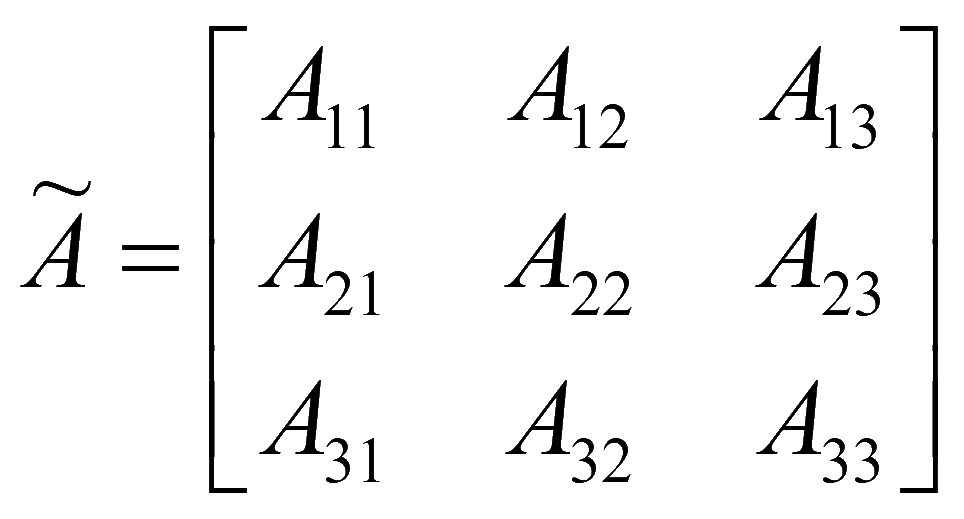
1. Определитель не изменится, если строки поменять местами со столбцами (транспонировать)

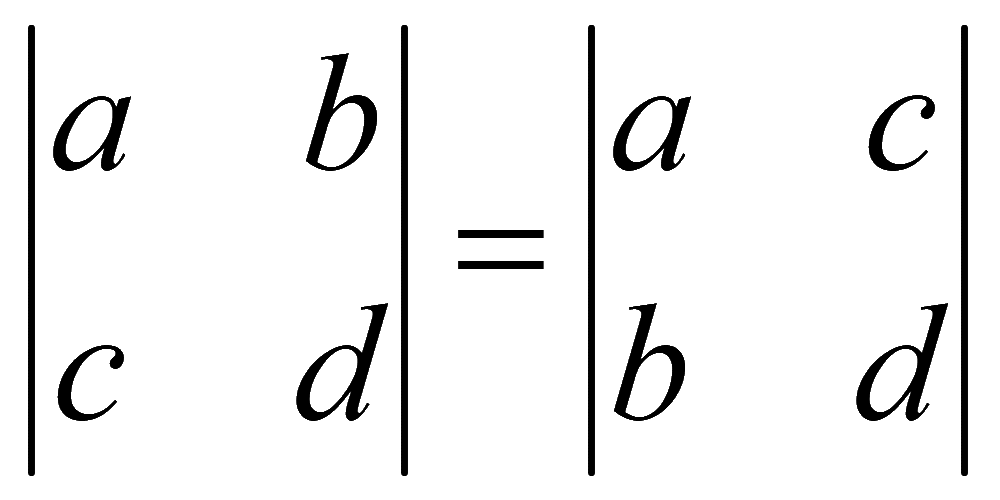
2. Если все элементы какой-либо строки (столбца) определителя равны нулю, то определитель равен нулю

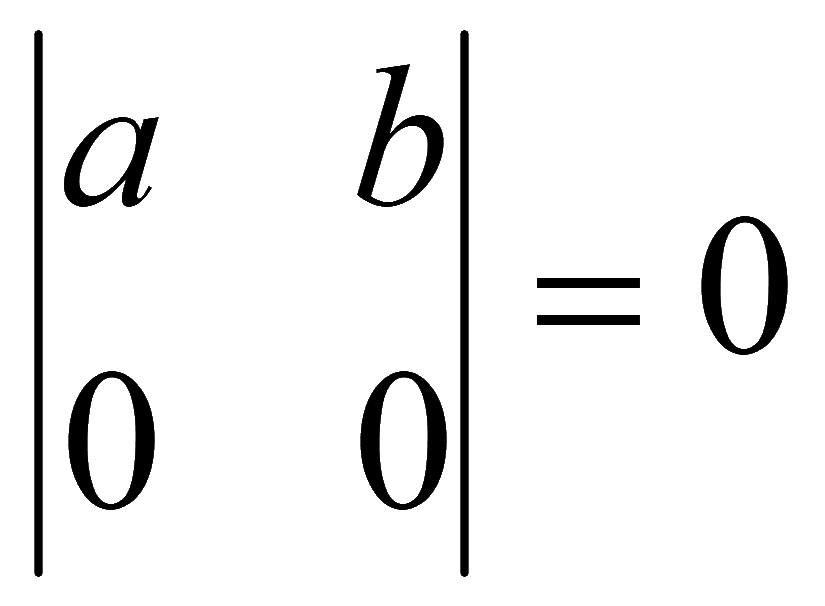
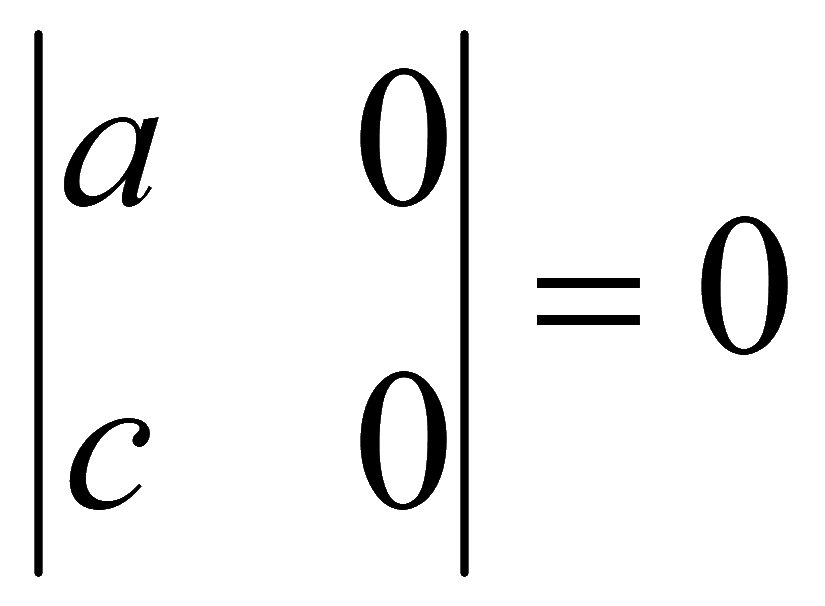
3. Если все элементы какой-либо строки (столбца) определителя умножить на число, то величина определителя умножится на это число (общий множитель какой-либо строки (столбца) можно выносить за определитель или осуществлять обратное действие)

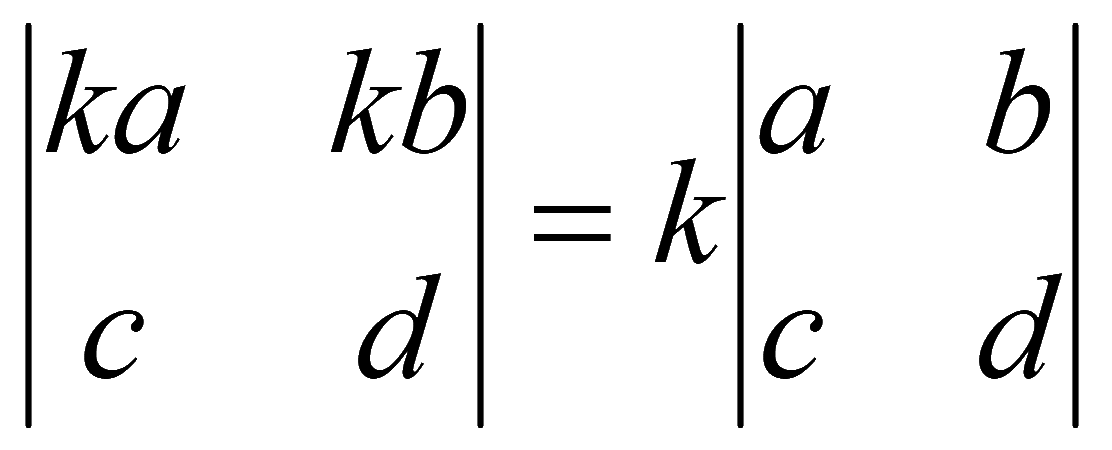
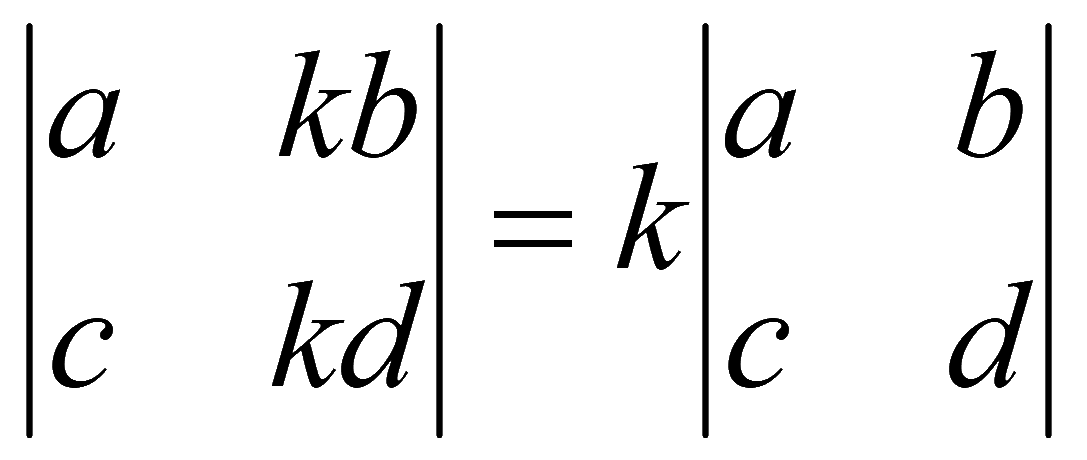
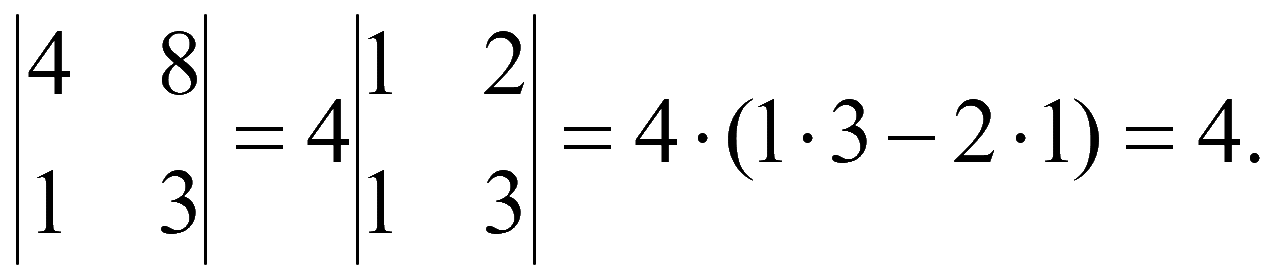
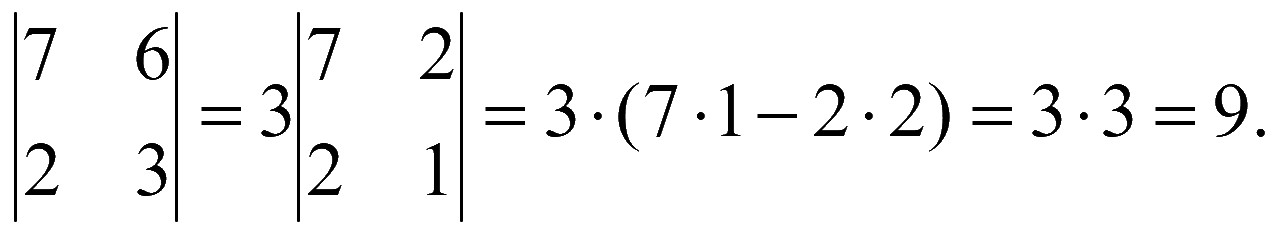
Если у элементов какой-либо строки (столбца) определителя поменять знак, то определитель также поменяет знак (минус у всех элементов какой-либо строки (столбца) можно выносить за определитель или производить обратное действие)

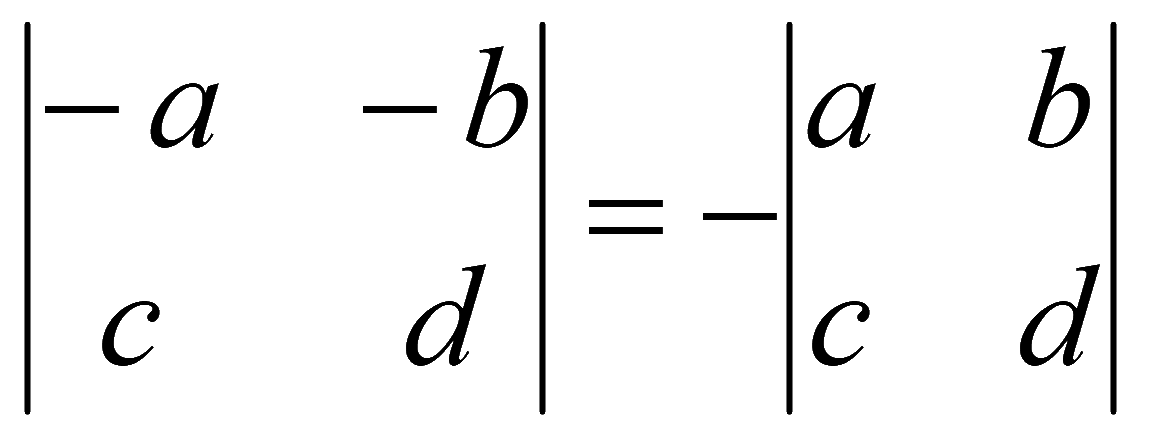
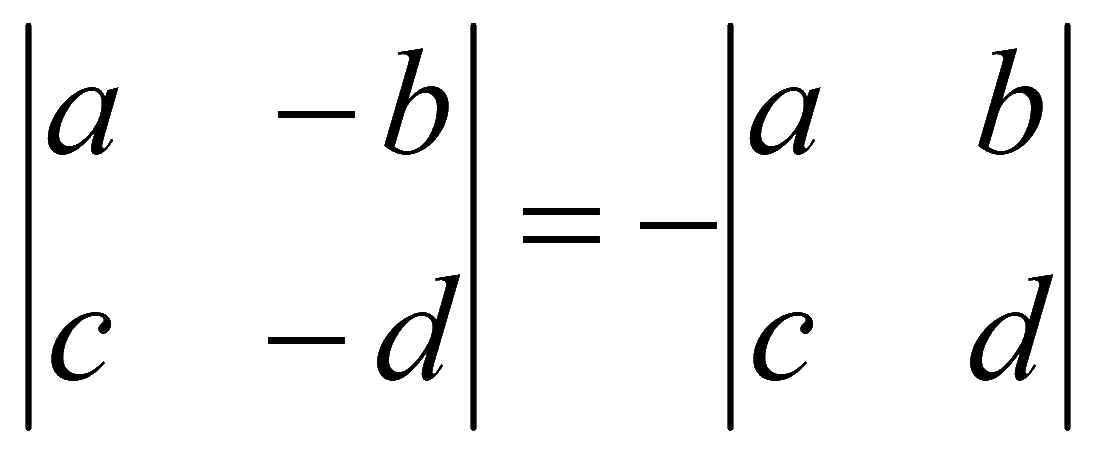
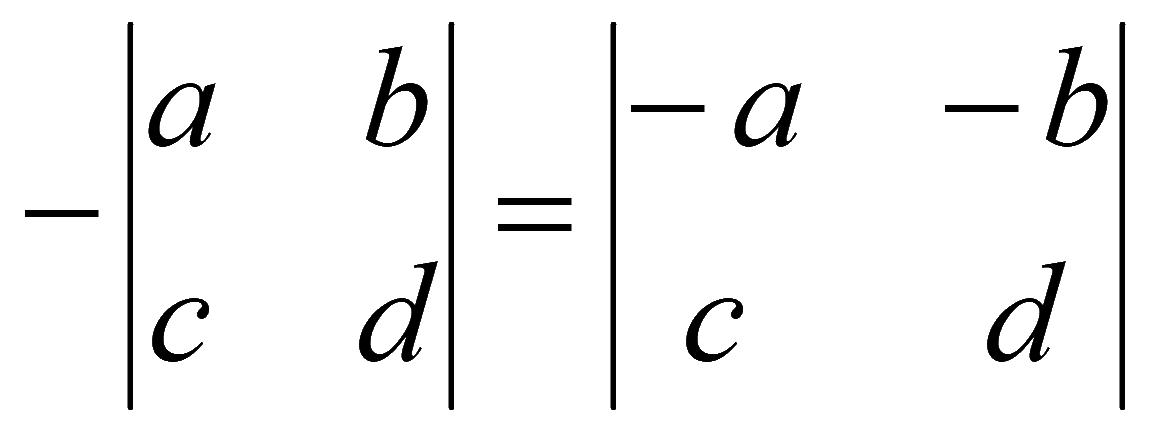
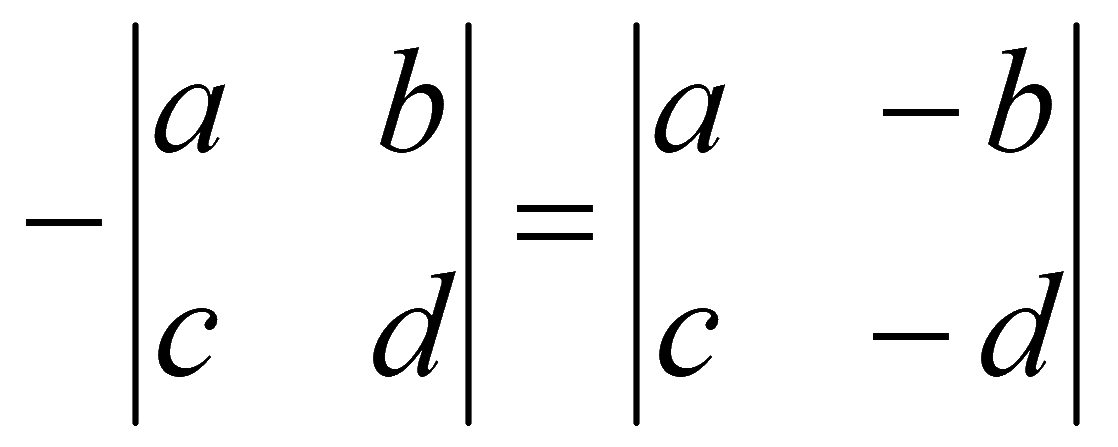
4. При перестановке двух любых строк (столбцов) величина определителя меняет знак на противоположный

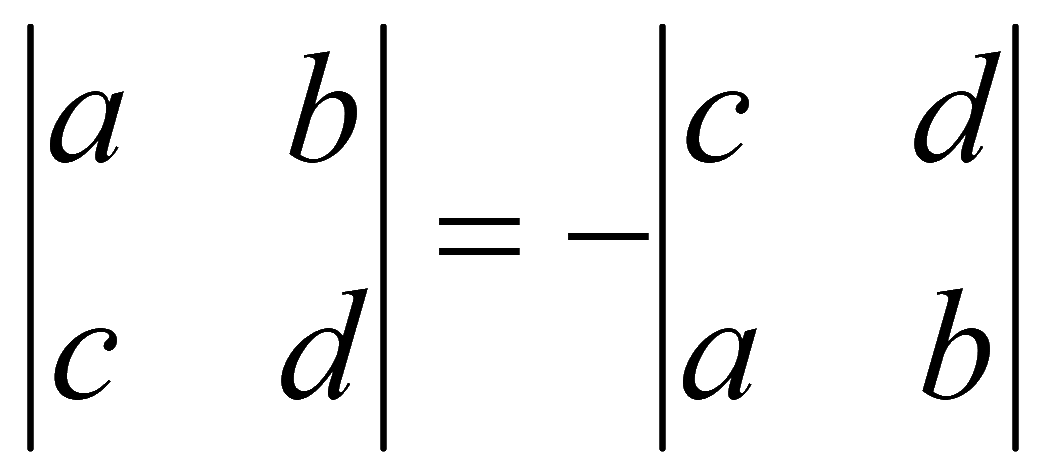
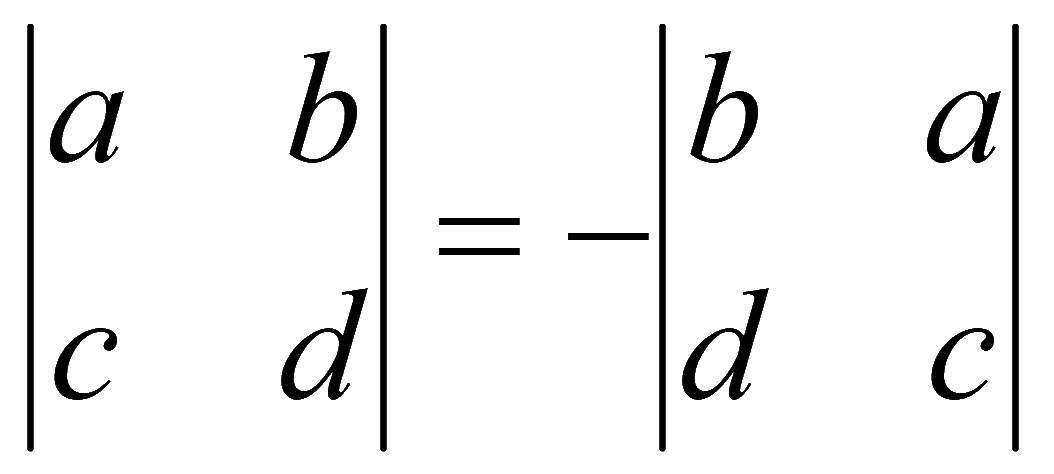
5. Если в определителе есть две одинаковые строки (столбца), то определитель равен нулю

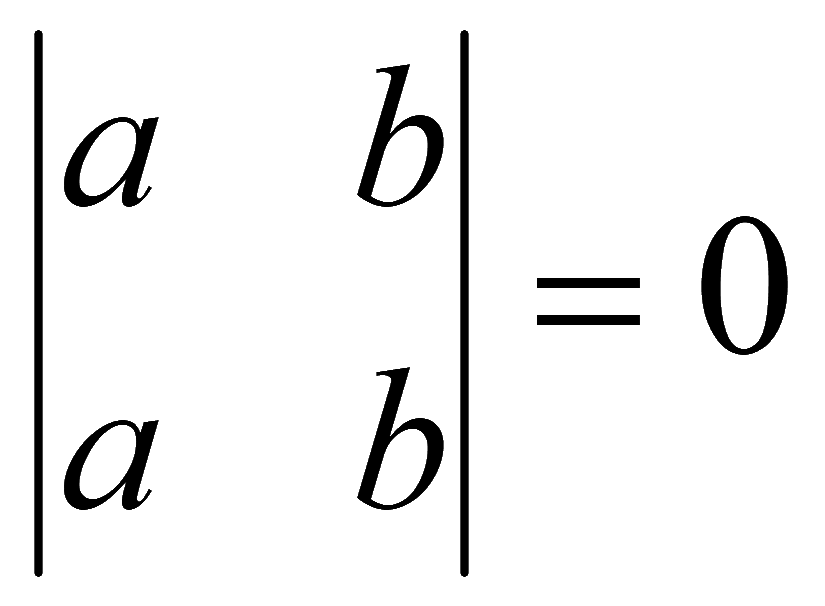
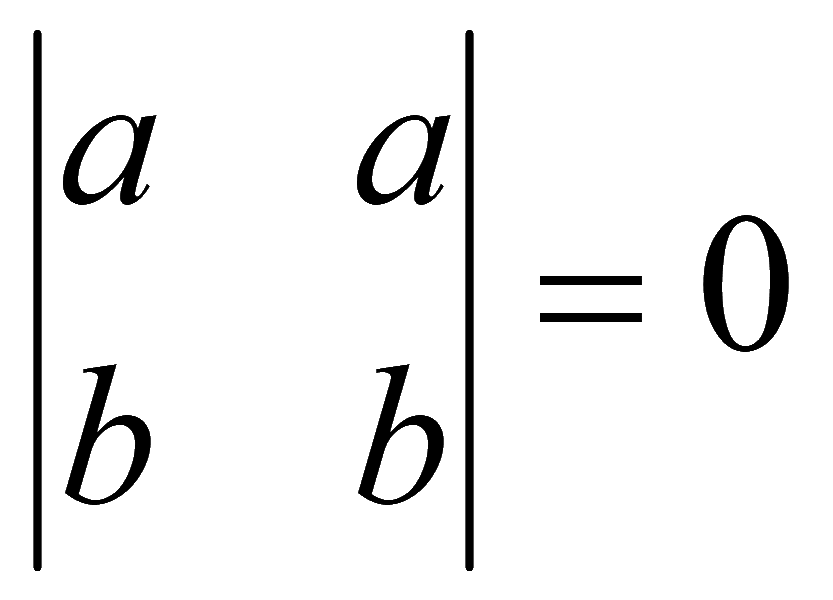
6. Если в определителе элементы какой-либо строки (столбца) пропорциональны соответствующим элементам другой строки (столбца), то определитель равен нулю

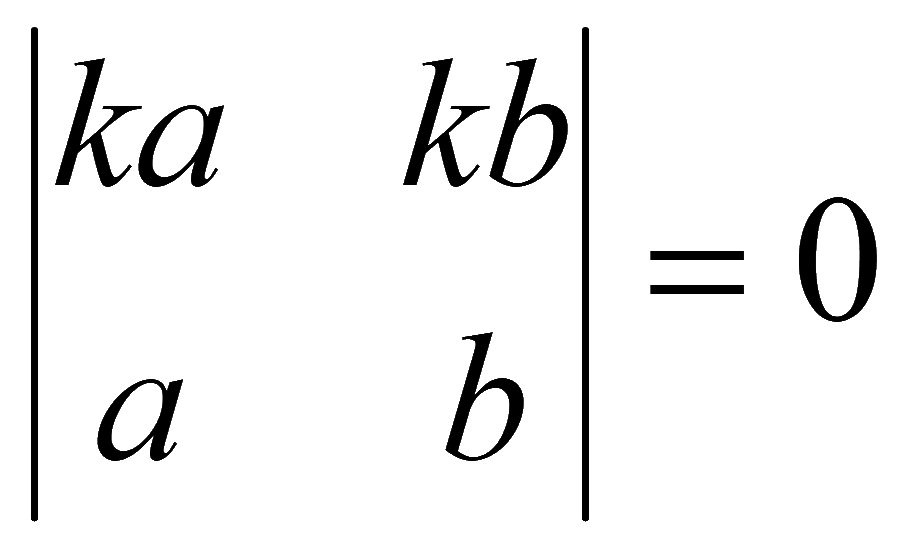
7. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число

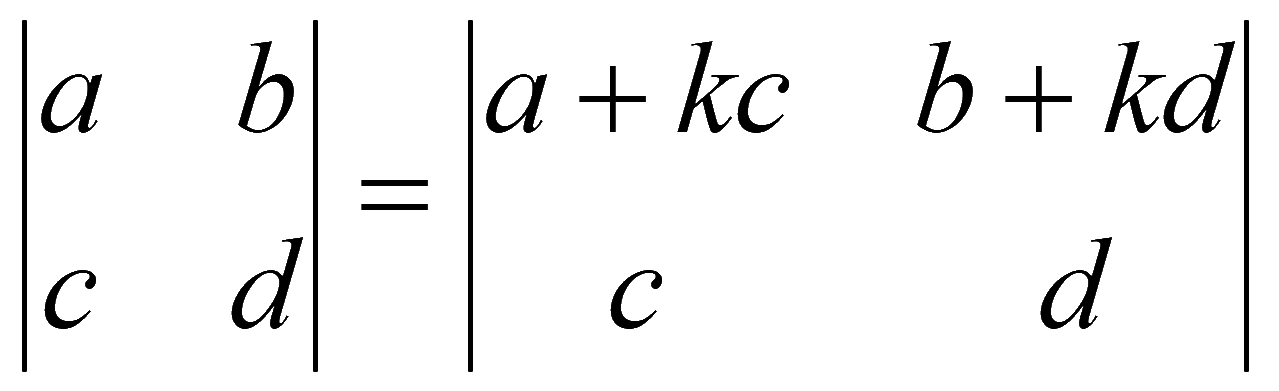
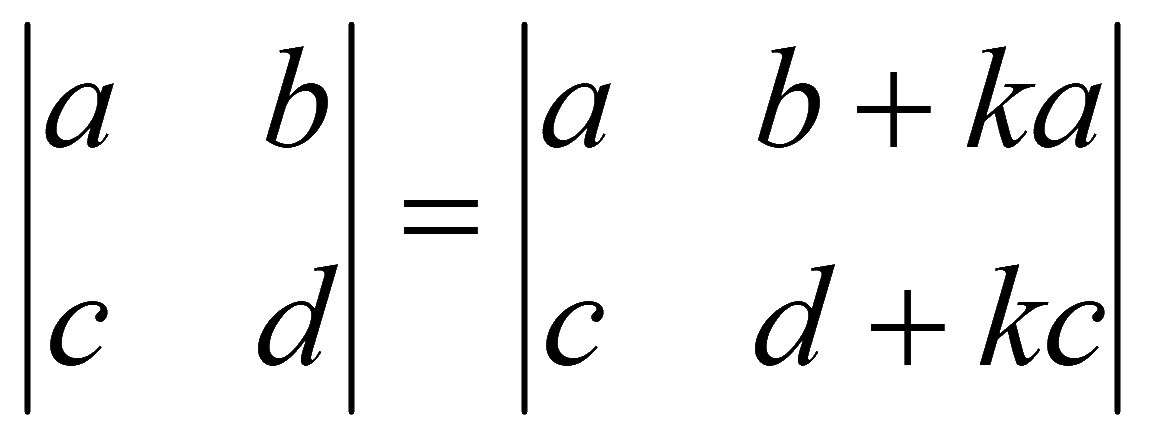
8. Определитель произведения двух квадратных матриц равен произведению их определителей

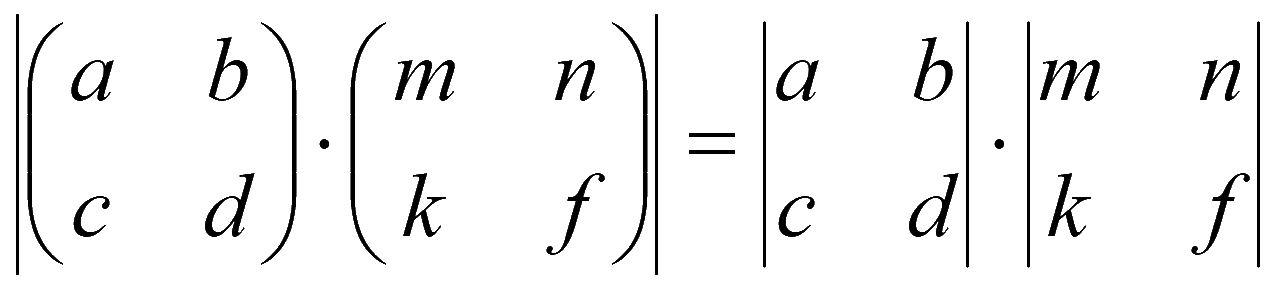
|AB| = |A||B|.

|A||B| = |AB|.

9. Если элементы какой-либо строки (столбца) определителя представлены в виде суммы двух чисел, то определитель равен сумме определителей, в каждом из которых соответствующая строка (столбец) содержит только одно слагаемое, а остальные строки (столбцы) те же, что и в исходном определителе.

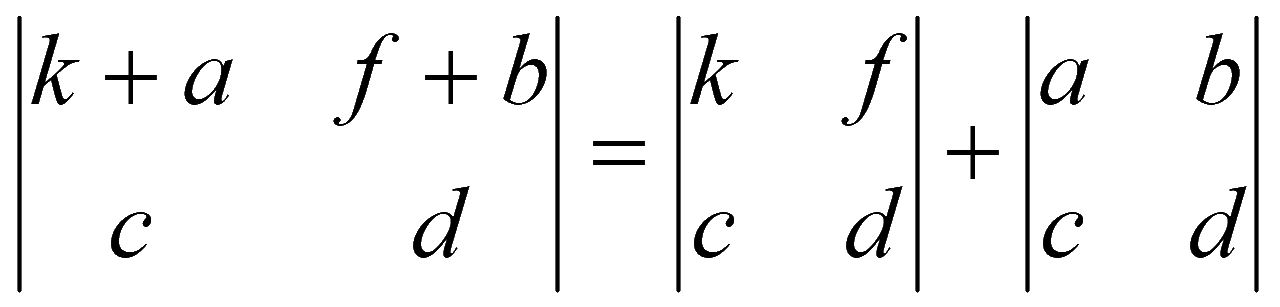
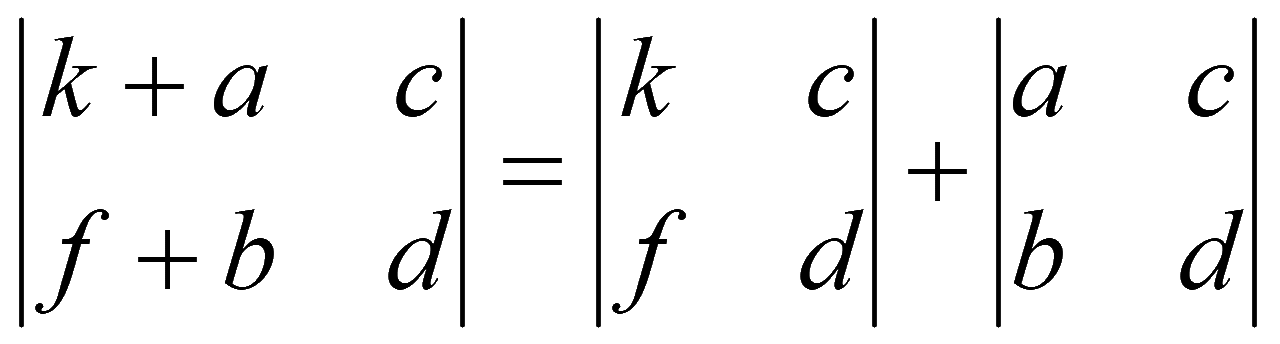
10. Если элементы какой-либо строки (столбца) определителя равны линейной комбинации соответствующих элементов каких-либо других строк (столбцов), то такой определитель равен нулю.

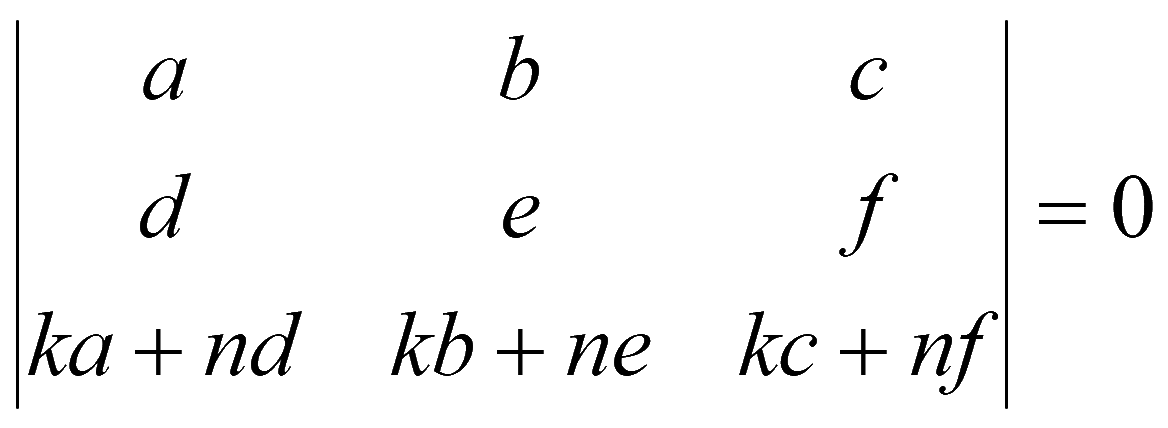
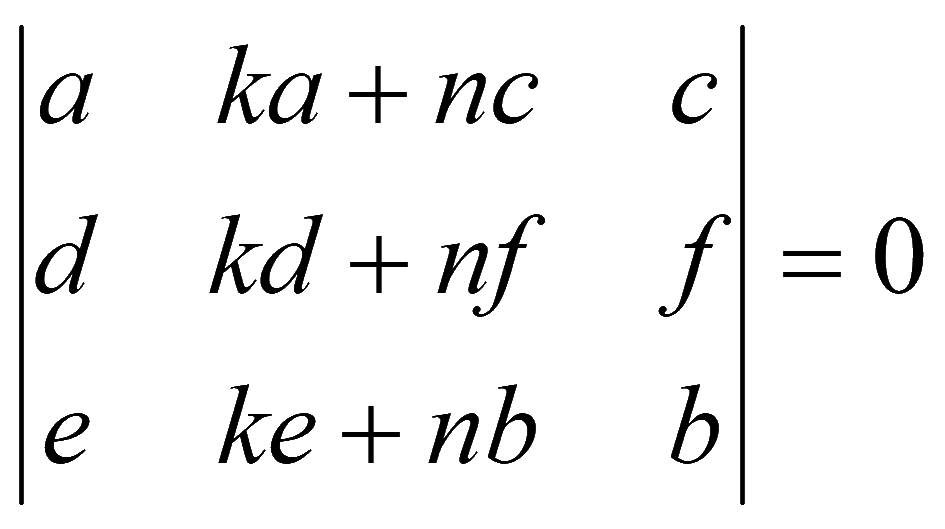
Теорема Лапласа. Величина определителя равна сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения. Разложение по элементам 1-й строки

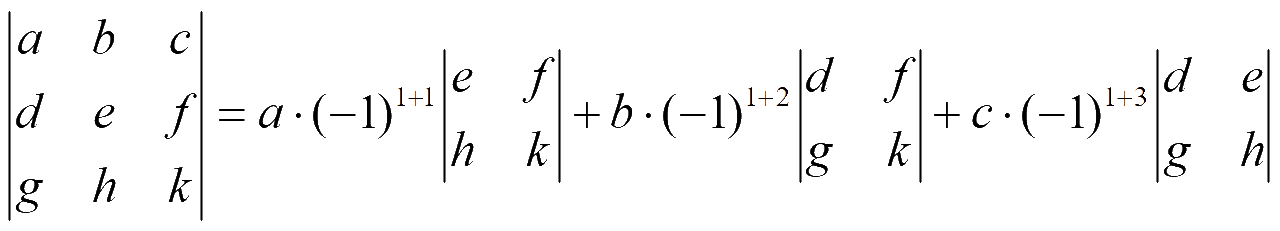
Разложение по элементам 1-го столбца

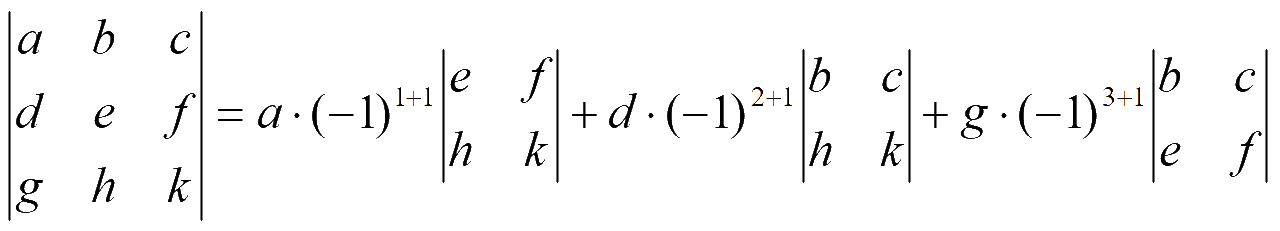
При нахождении определителя разлагать лучше по элементам той строки или столбца, которые содержат больше нулей или единиц (произведение с единицей или нулем проще произвести).

Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю.

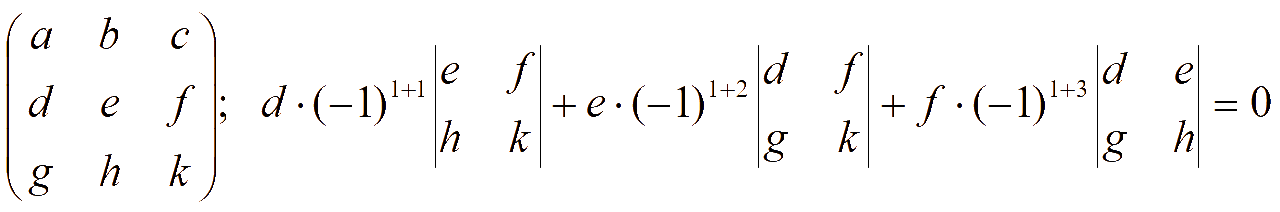
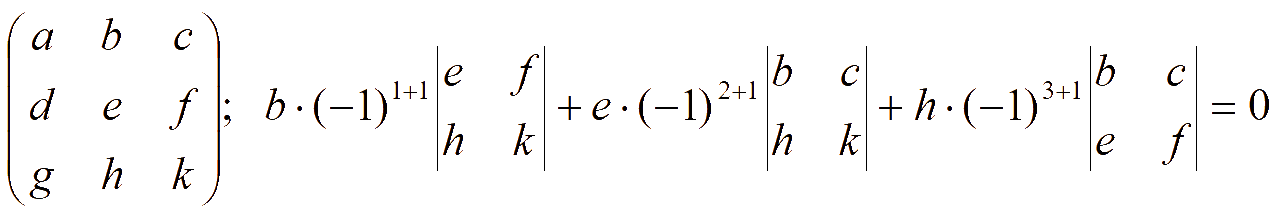
Пример. Найдем определитель 2-го порядка, разложив его по элемента 1-й строки:

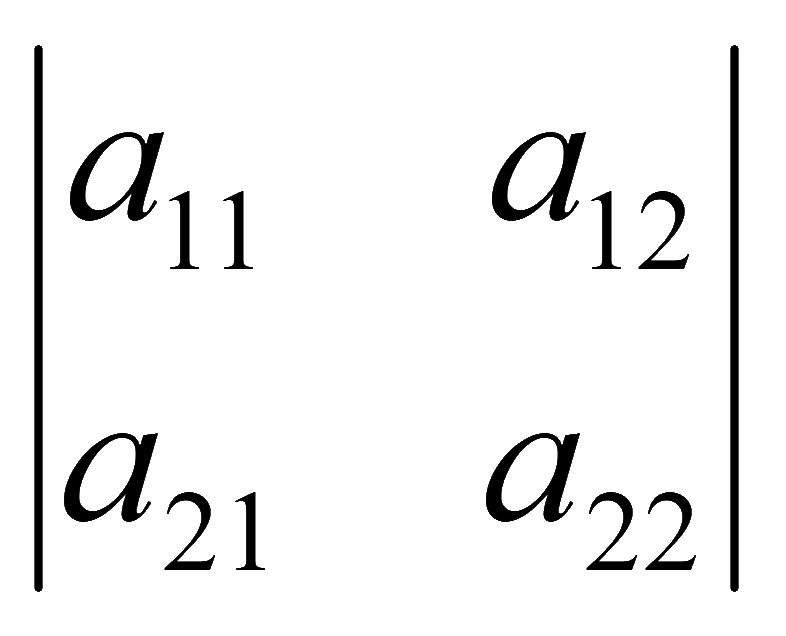= a₁₁(-1)¹⁺¹М₁₁ + a₁₂(-1)¹⁺²М₁₂ =

= a₁₁(-1)¹⁺¹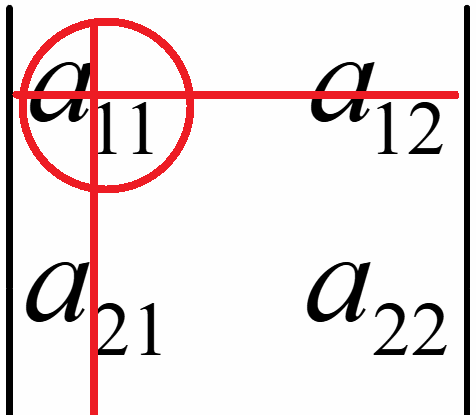 + a₁₂(-1)¹⁺² =

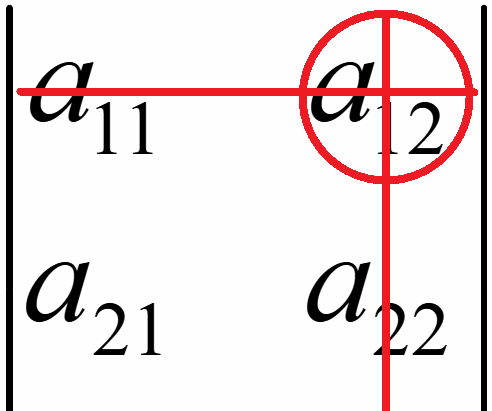= a₁₁(-1)¹⁺¹a₂₂ + a₁₂(-1)¹⁺²a₂₁ = a₁₁a₂₂ - a₁₂a₂₁.

Пример. Найдем определитель, разложив его по элемента 1-й строки:

=

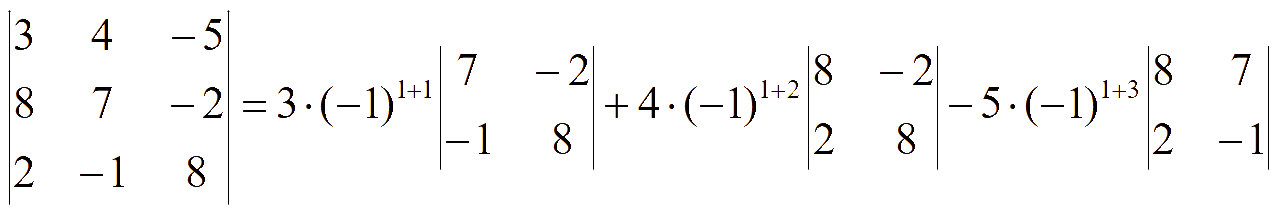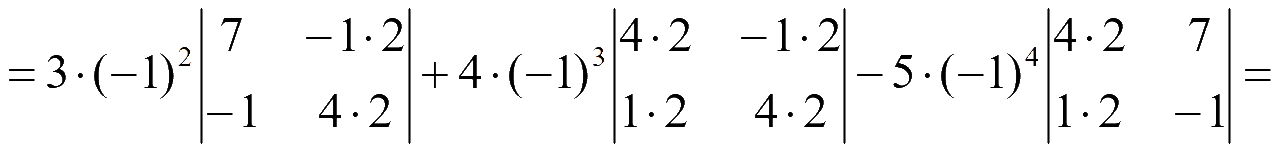
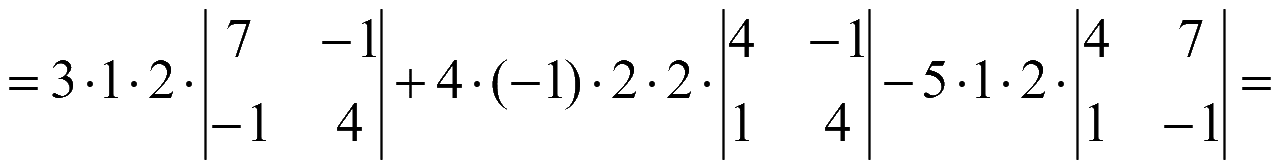
= 6·(7·4-(-1)·(-1))-16·(4·4-(-1)·1)-10·(4·(-1)-7·1) =

= 6·(28-1)-16·(16+1)-10·(-4-7) = 6·27-16·17-10·(-11) =

= 6·27-16·17+10·11 = 2·(3·27-8·17+5·11) = 2·(81-136+55) = 0.

Пример

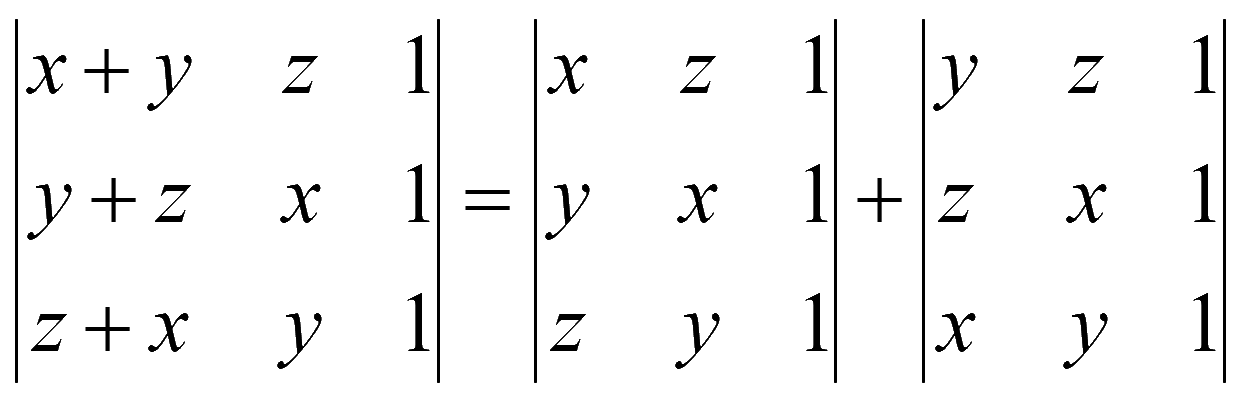
Каждый определитель из полученной суммы целесообразно находить путем разложения по элементам 3-го столбца, состоящего лишь из единиц.

Задача. Найти определитель

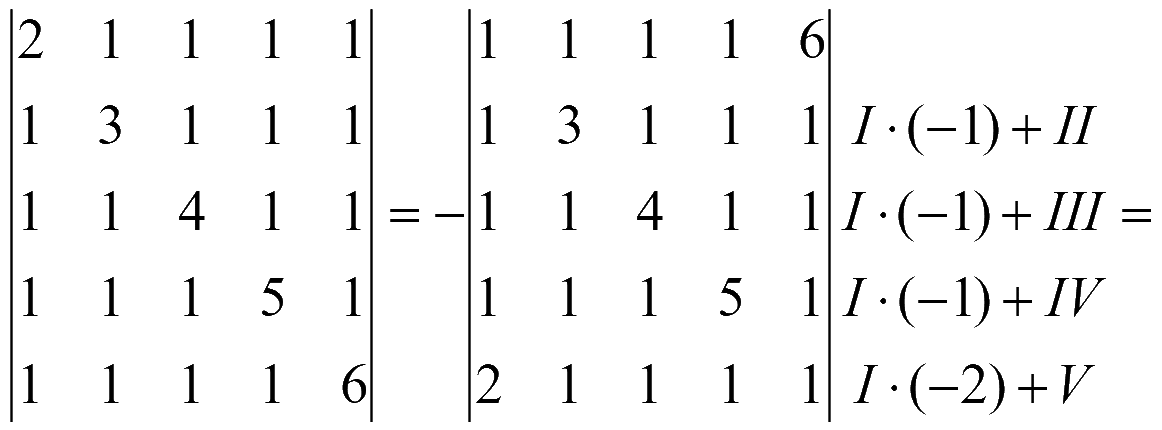
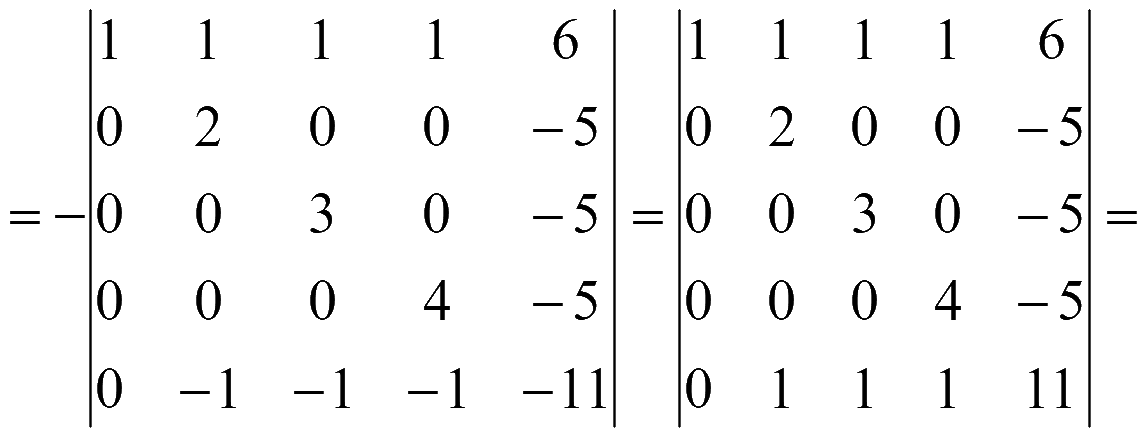
= {поменяем 2-ю и 5-ю строки, поменяв знак определителя} =

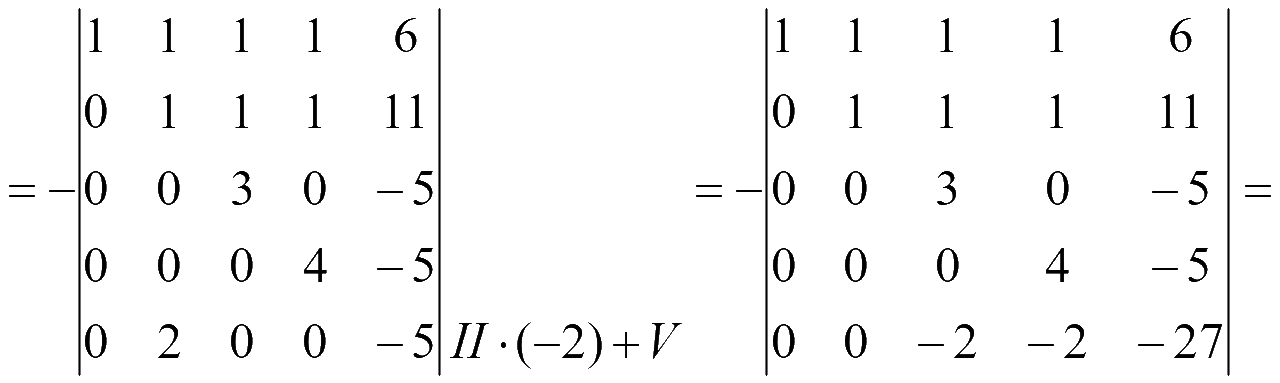
= {поменяем 3-ю и 5-ю строки, поменяв знак определителя} =

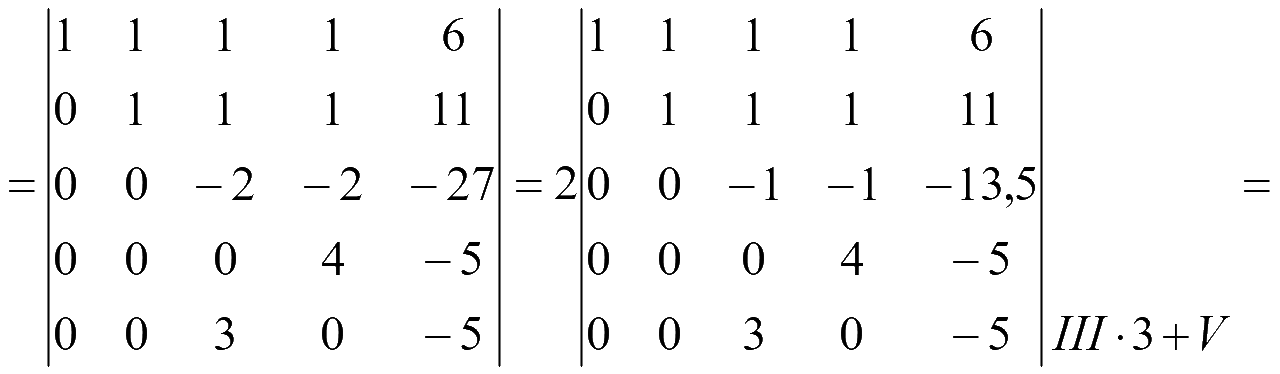
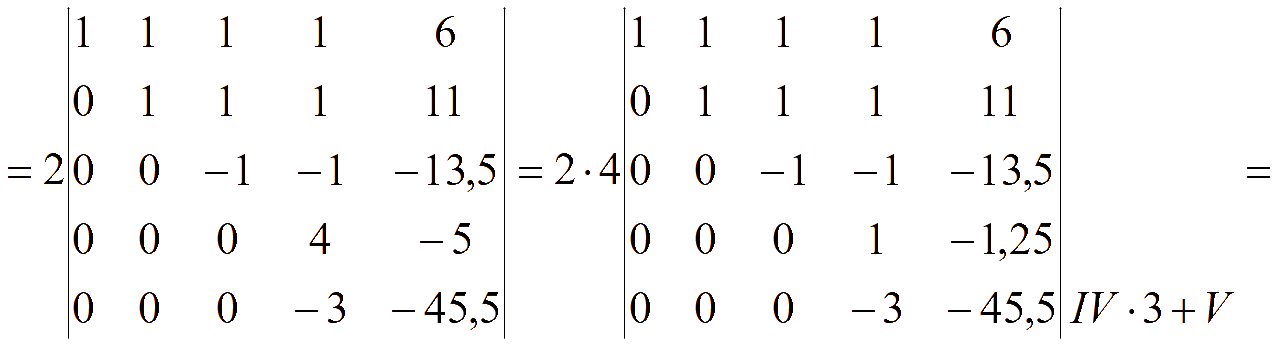
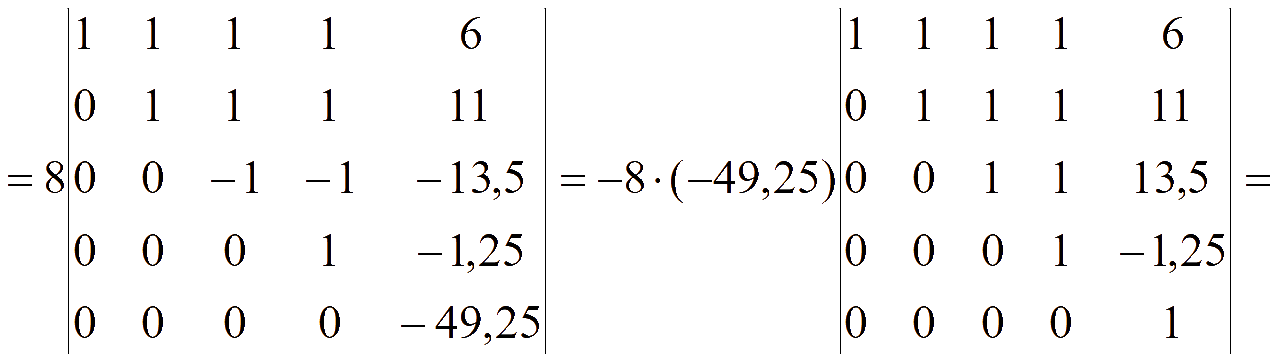
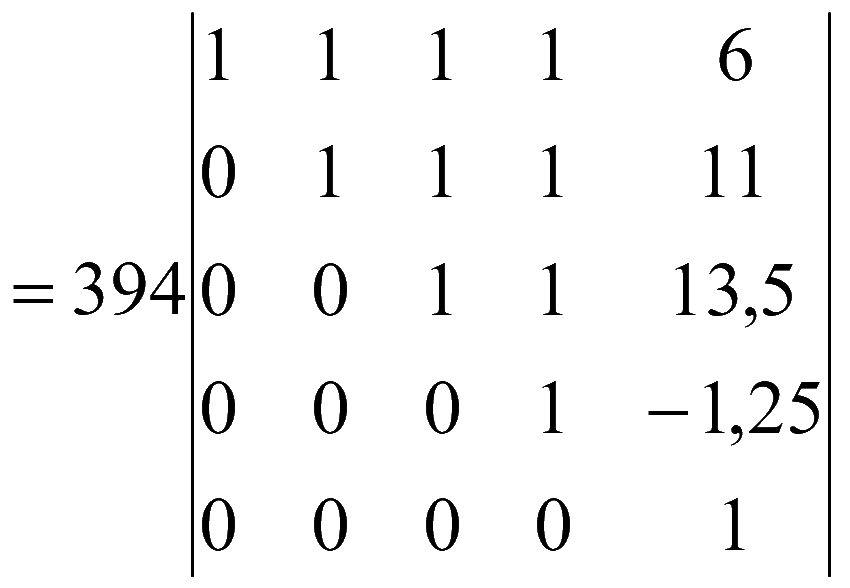
Для вычисления определителя всякий раз будем разлагать по элементам первого столбца, который содержит 1 и нули

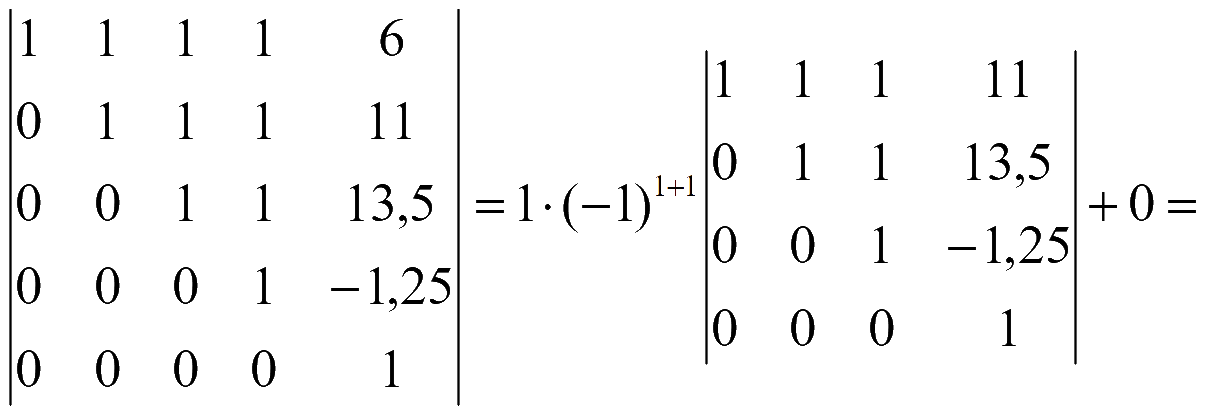
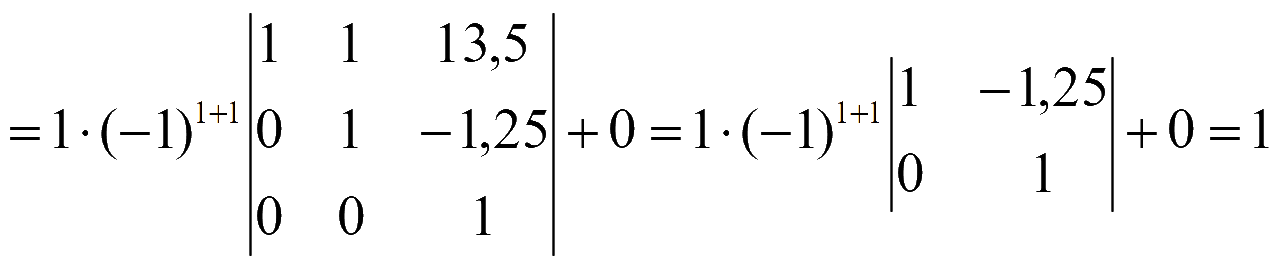
Ответ: 394.

Задача 1.2.45 [1]

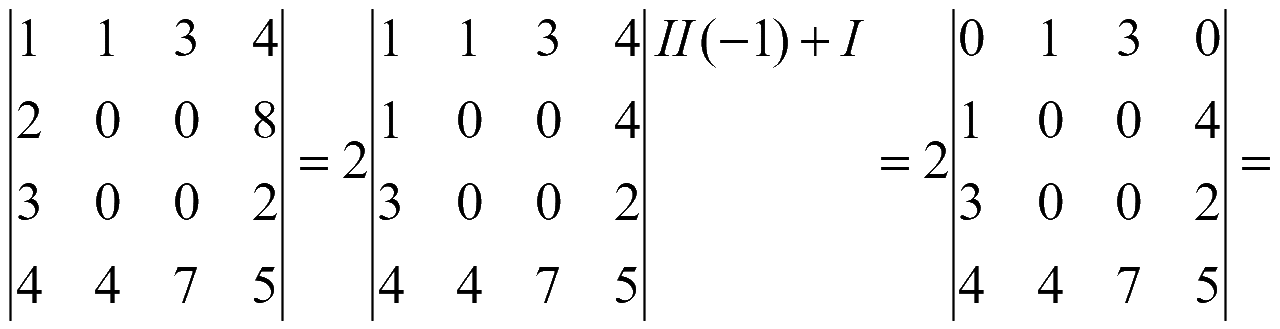
= {разложим по элементам первой строки} =

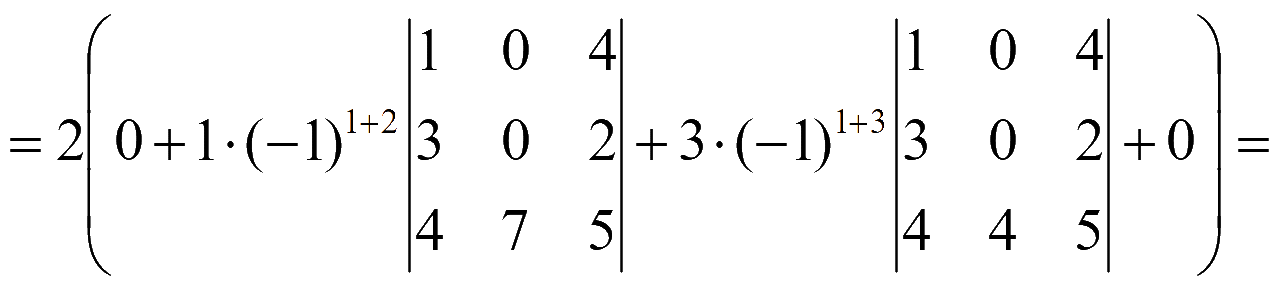
= {разложим оба определителя по элементам второго столбца} =

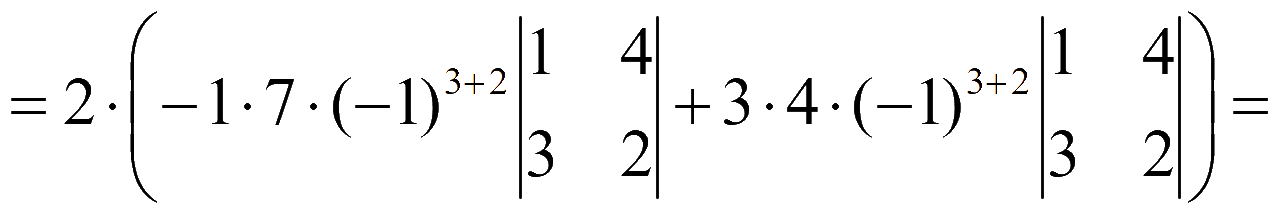
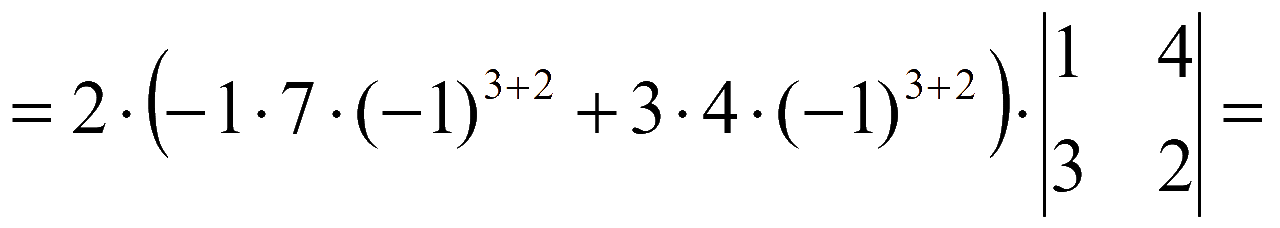
= 2·(7 - 12)·(1·2 - 4·3) = 2·(-5)·(-10) = 2·50 = 100.

8 Обратная матрица

Для квадратной матрицы A можно найти обратную матрицу

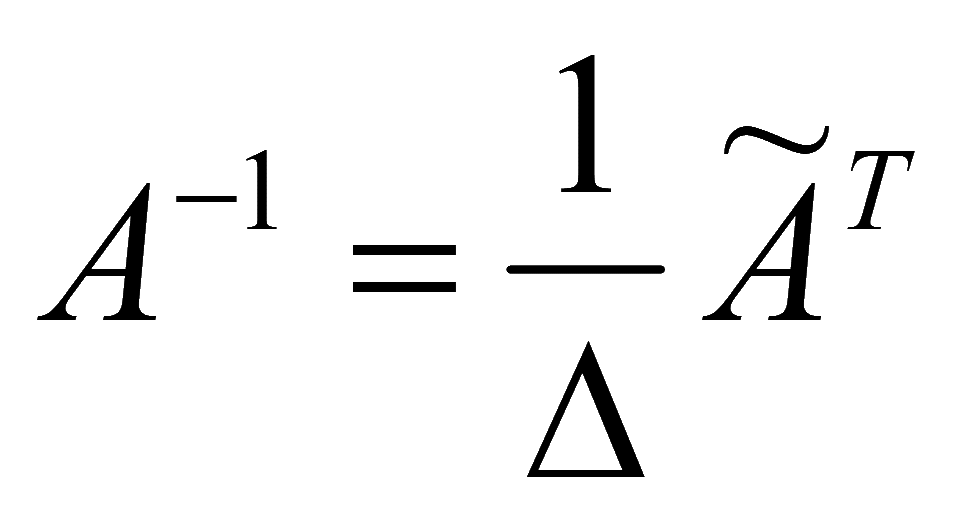
где Δ — определитель матрицы A;

- союзная матрица, составленная из алгебраических дополнений элементов матрицы A.

- транспонированная союзная матрица.

8.1 Нахождение обратной матрицы методом Жордана

К матрице системы A добавляем справа единичную матрицу такого же размера. Затем эквивалентными преобразованиями над строками добиваемся получения единичной матрицы слева, тогда справа получится обратная матрица

(A|E) ~ (E|A^-1).

Если к матрице системы A добавить снизу единичную матрицу такого же размера.

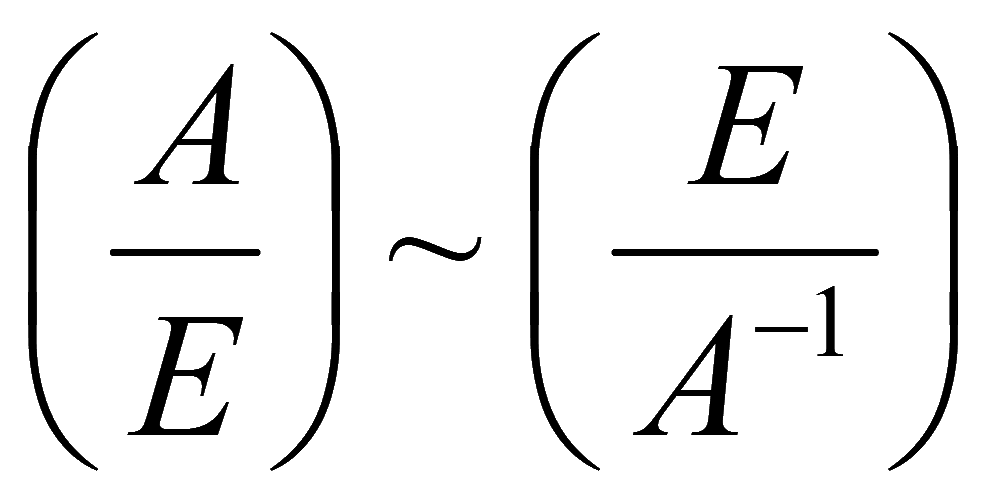
Затем эквивалентными преобразованиями над столбцами добиваемся получения единичной матрицы сверху, тогда снизу получится обратная матрица

.

9 Невырожденные линейные системы уравнений

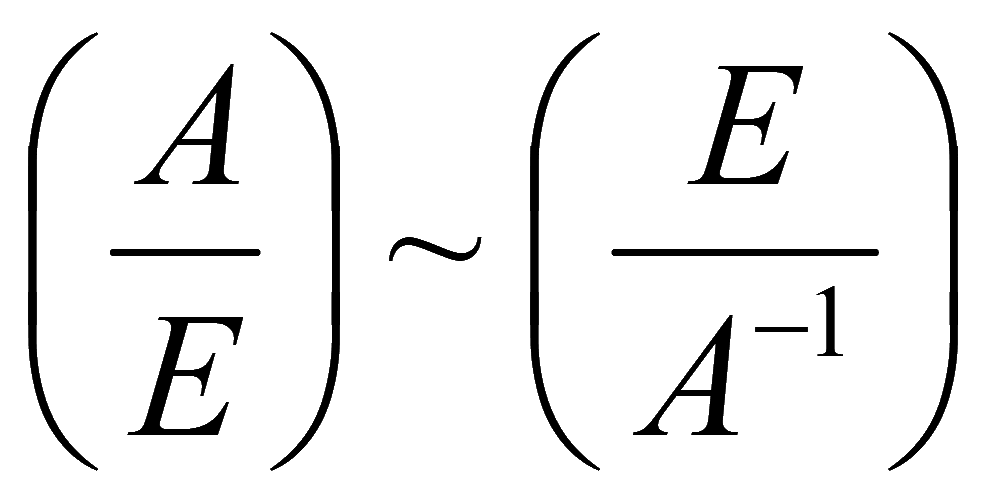Линейная система уравнений является невырожденной, если ее определитель не равен нулю Δ ≠ 0.

9.1 Ранг матрицы

Рангом матрицы A называется наибольший порядок минора данной матрицы не равный нулю. Ранг матрицы A обозначается r, r(A) или rang A и находится в интервале

0 ≤ rang A ≤ min(m; n).

Миноры, порядок которых определяет ранг матрицы, называются базисными.

Задача № 611. Решить систему уравнений [2]

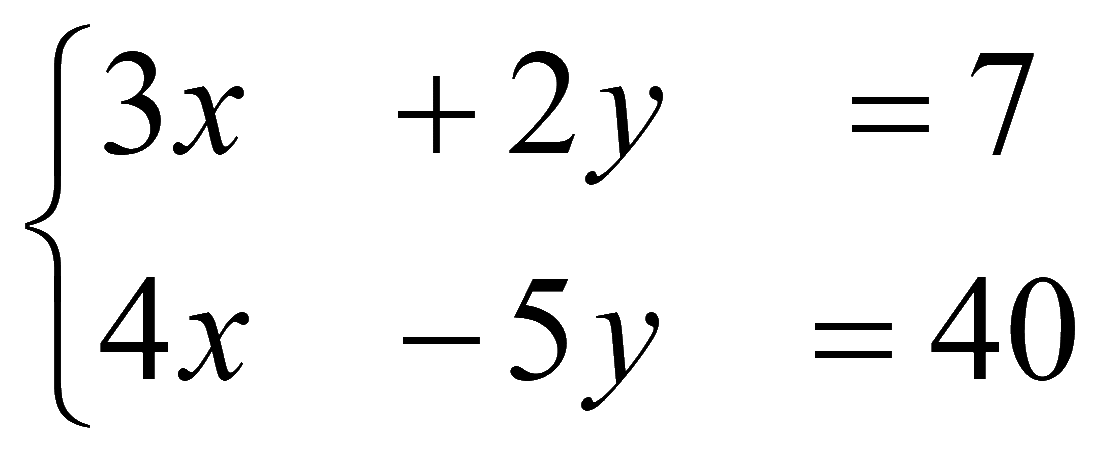
Решение

Метод Гаусса - 1-й способ

Расширенная матрица системы

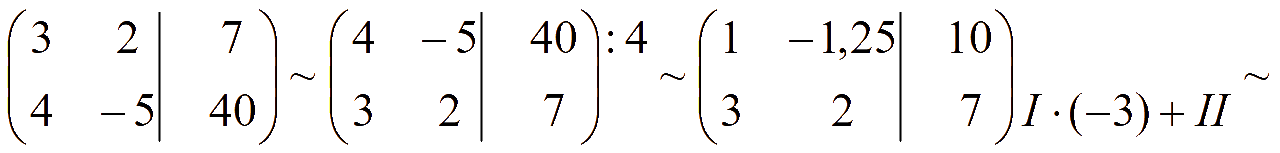
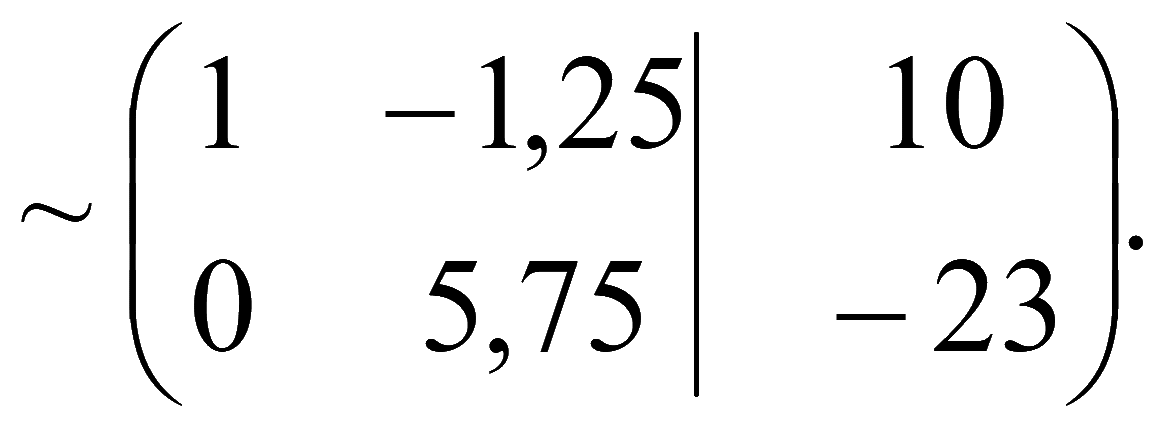
Соответствующая система уравнений

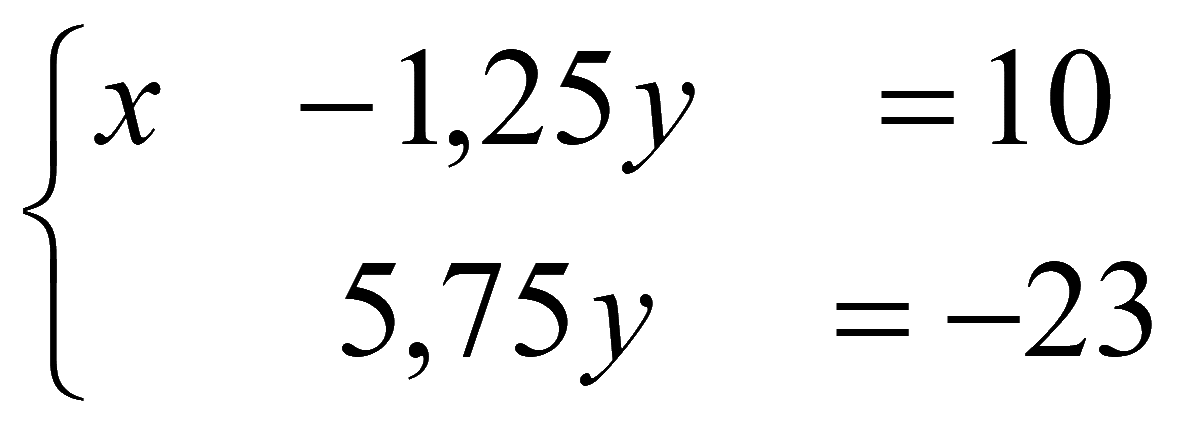
Решаем снизу вверх

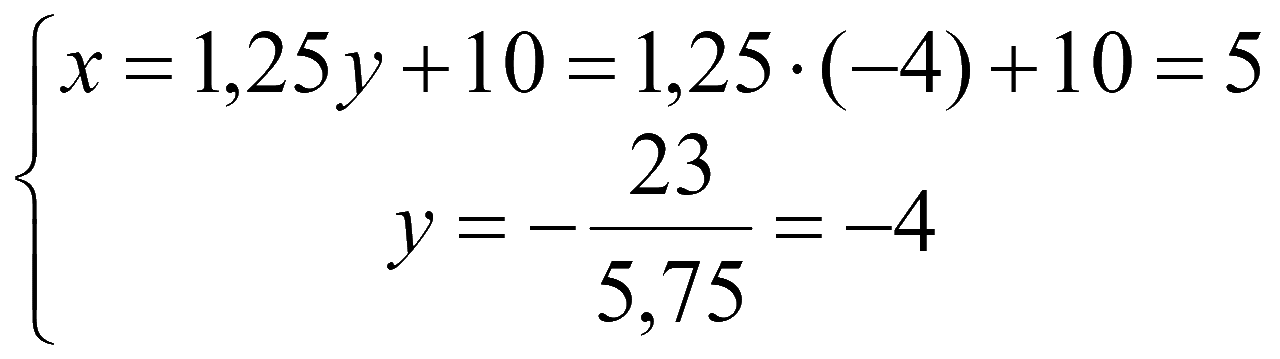
Матричный метод (метод обратной матрицы) - 2-й способ

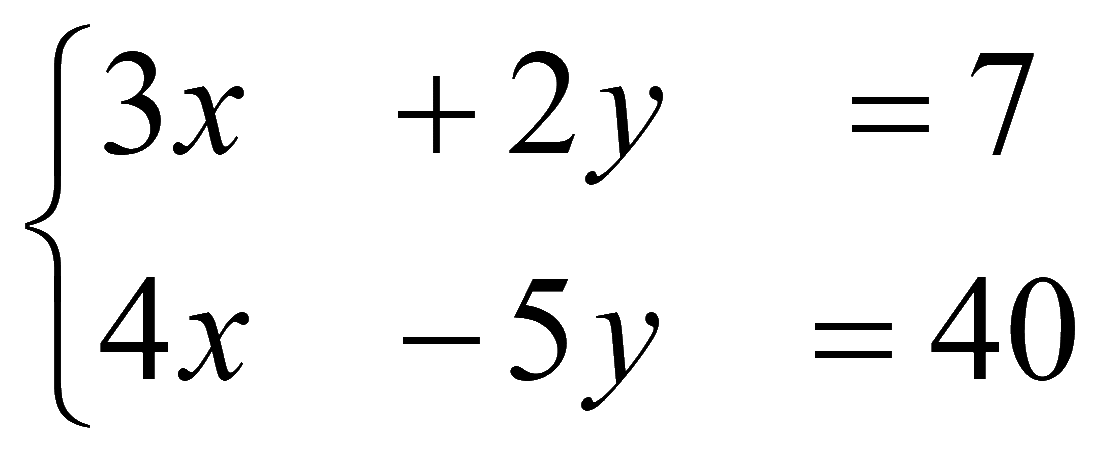
Матрица системы

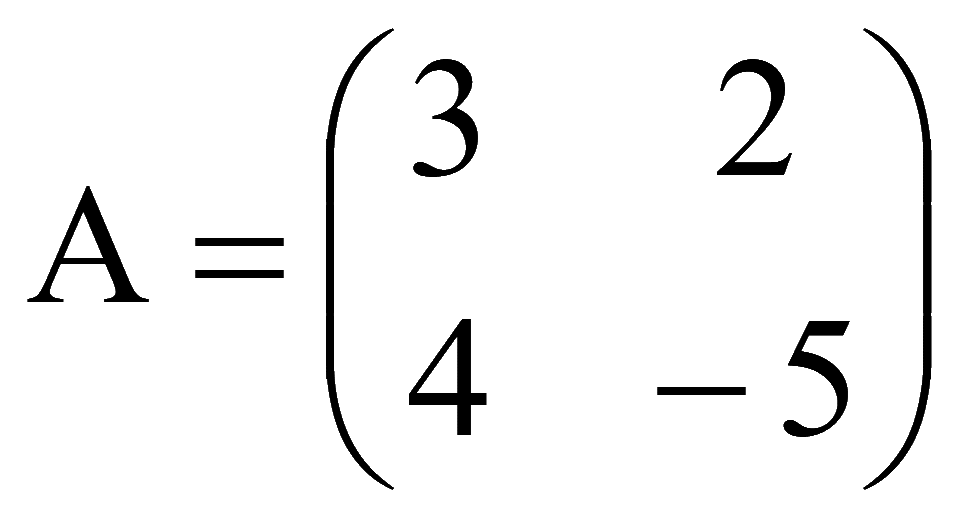
Матрица-столбец неизвестных

Матрица-столбец свободных членов

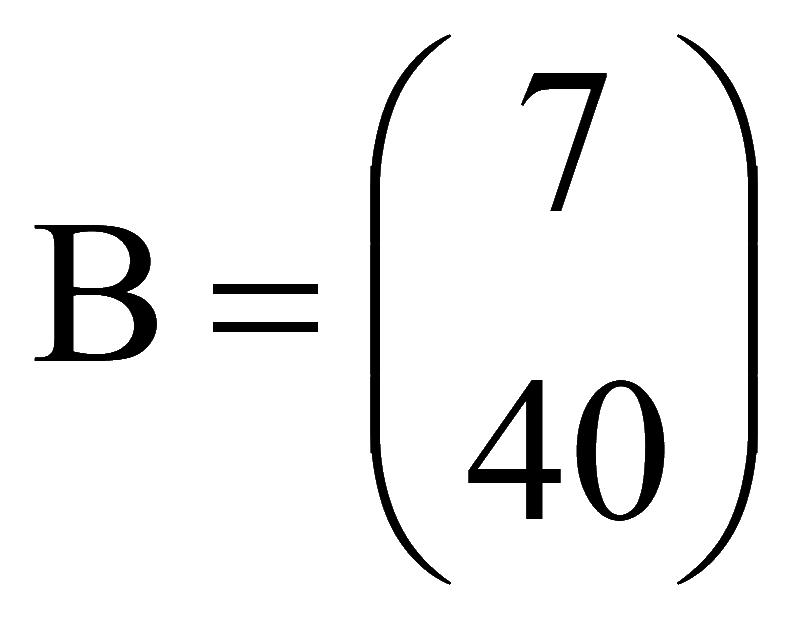
Запишем систему уравнений в матричном виде

AX = B

Решение ищем в виде

X = A^-1B

1-й способ нахождения обратной матрицы

Обратная матрица

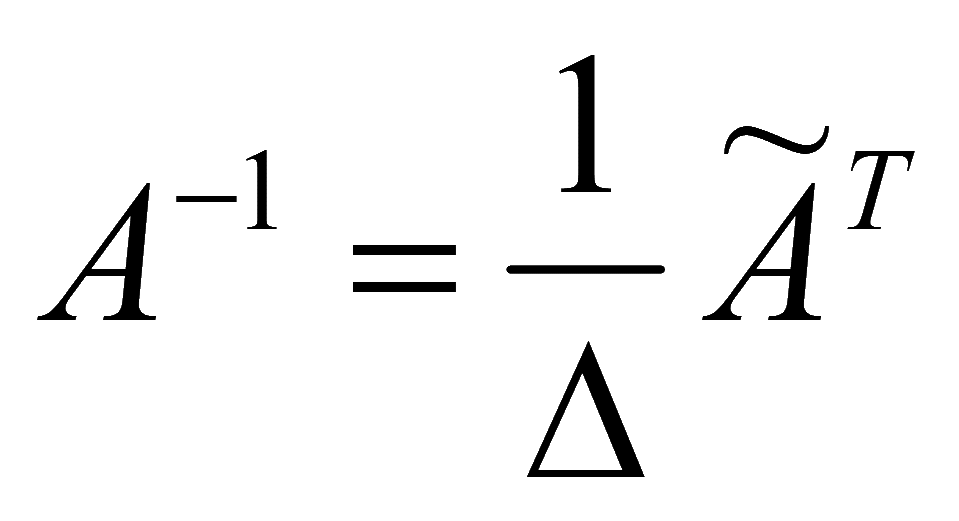
Находим определитель матрицы системы A

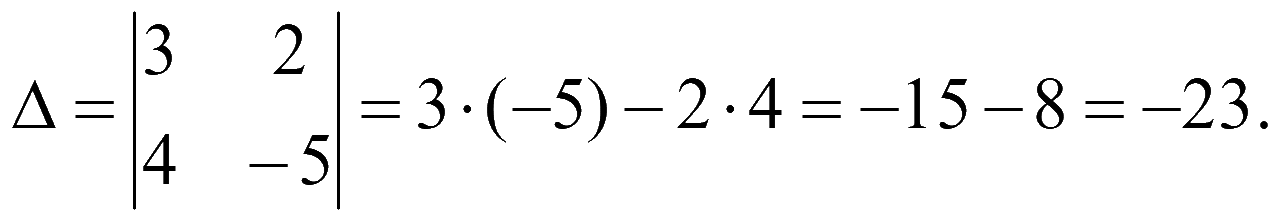
Находим матрицу алгебраических дополнений для матрицы

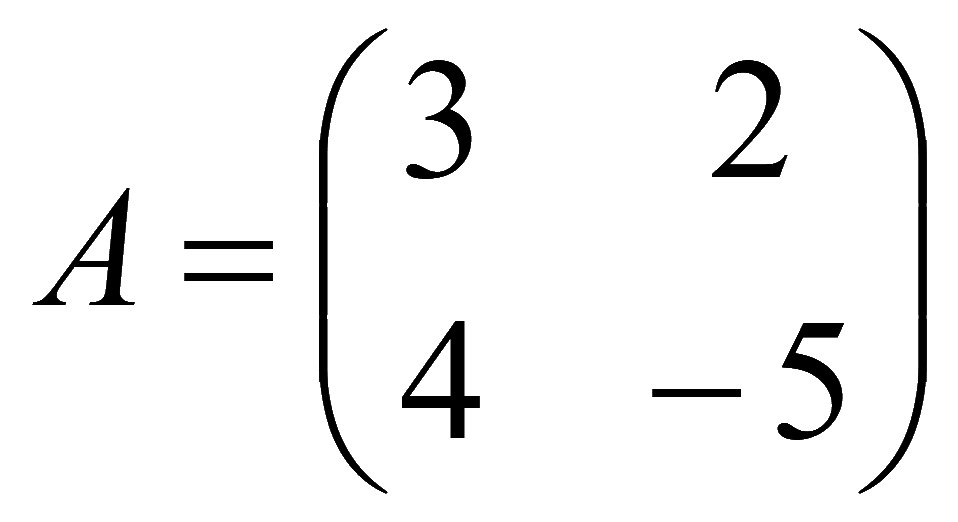
Из алгебраических дополнений составляем союзную матрицу

A₁₁ = (-1)¹⁺¹M₁₁ = (-1)²·(-5) = -5.

A₁₂ = (-1)¹⁺²M₁₂ = (-1)³·4 = -4.

A₂₁ = (-1)²⁺¹M₂₁ = (-1)³·2 = -2.

A₂₂ = (-1)²⁺²M₂₂ = (-1)⁴·3 = 3.

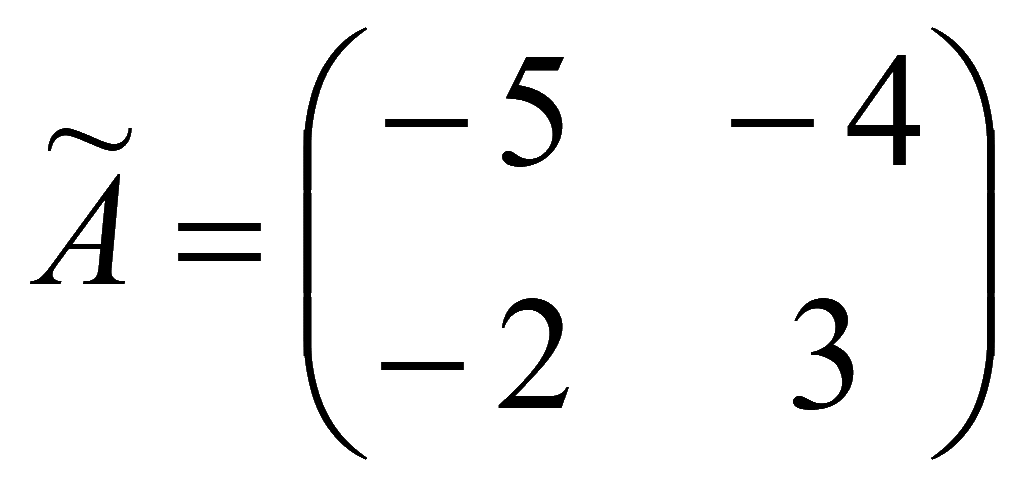
Транспонируем союзную матрицу

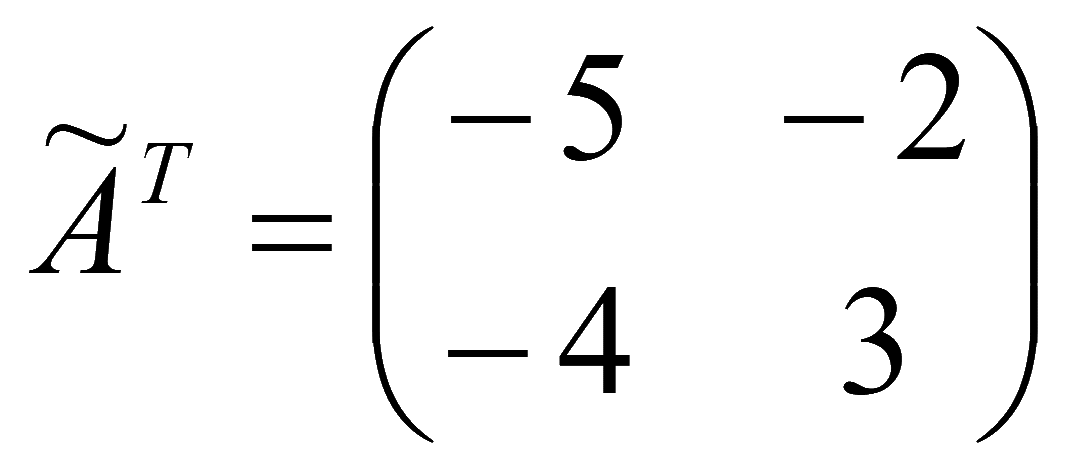
Обратная матрица

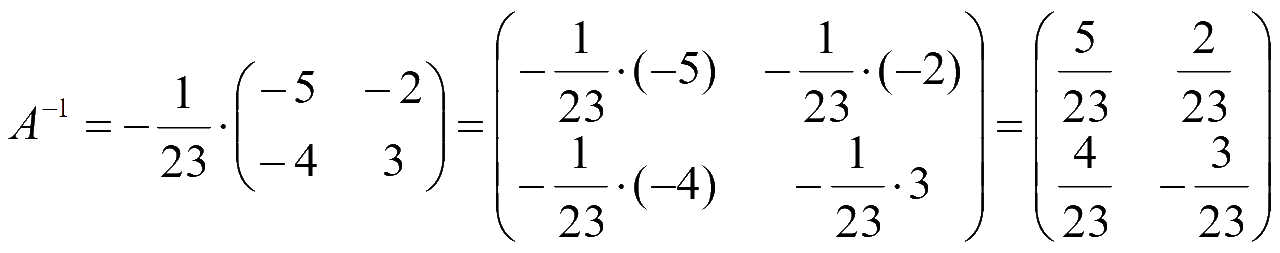
Умножение обратной матрицы на столбец свободных членов дает решение системы

A^-1B = X

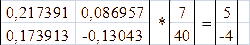
Матрица-столбец решений системы

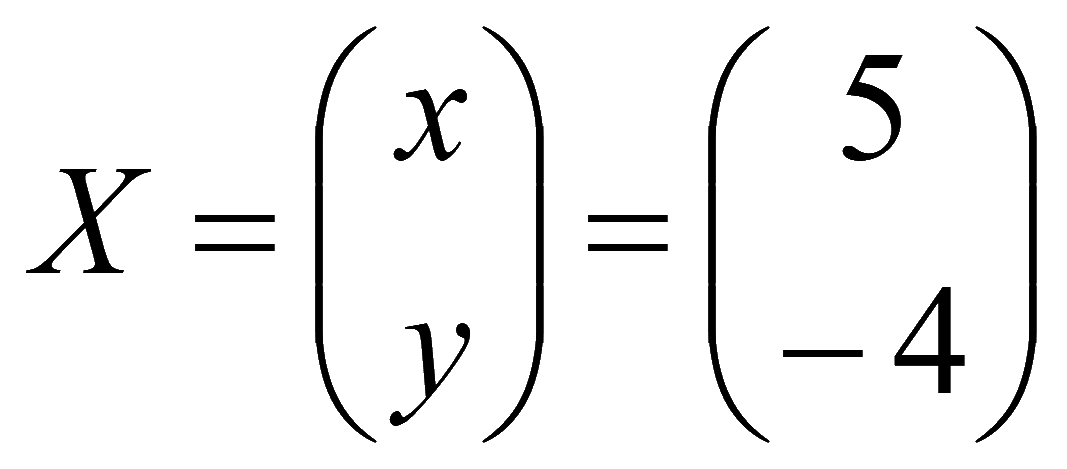
2-й способ нахождения обратной матрицы методом Жордана

К матрице системы A добавляем справа единичную матрицу такого же размера. Затем эквивалентными преобразованиями над строками добиваемся получения единичной матрицы слева, тогда справа получится обратная матрица

(A|E) ~ (E|A^-1).

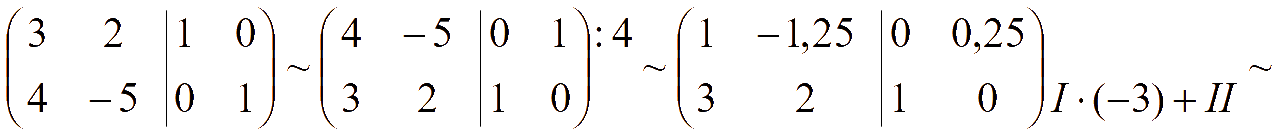
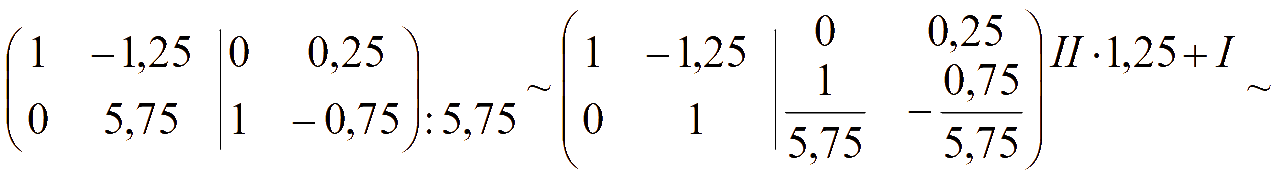
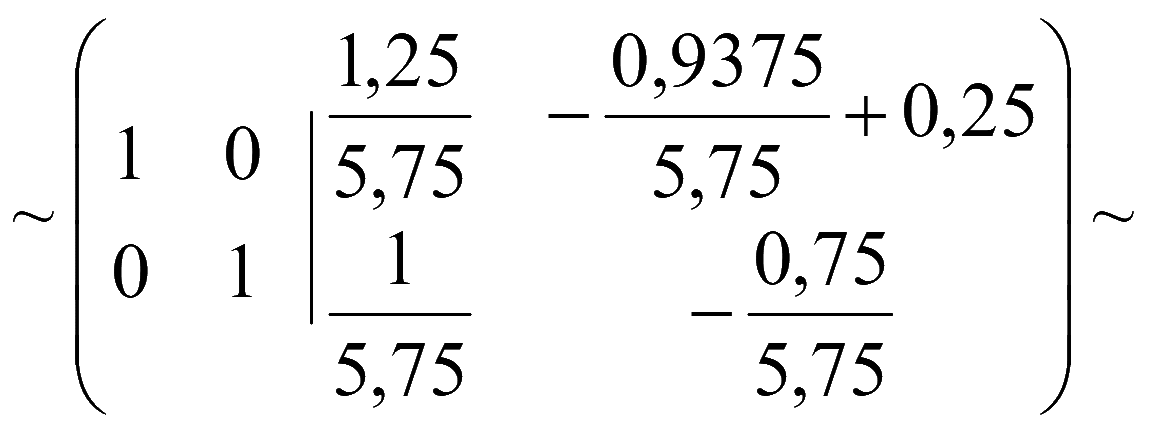
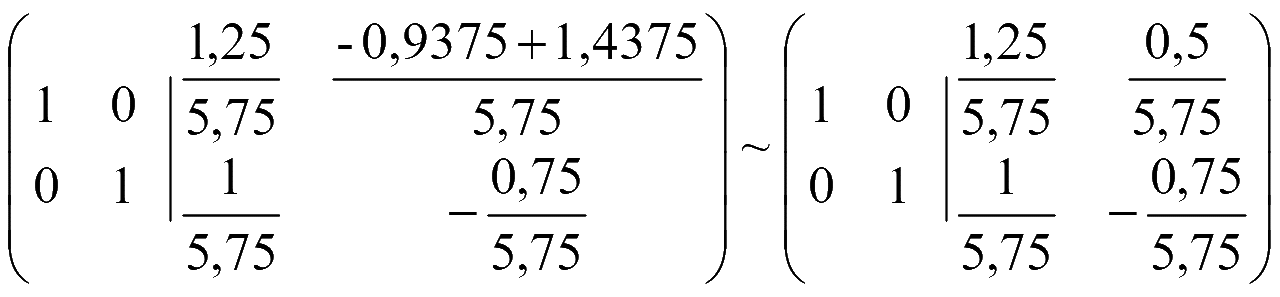
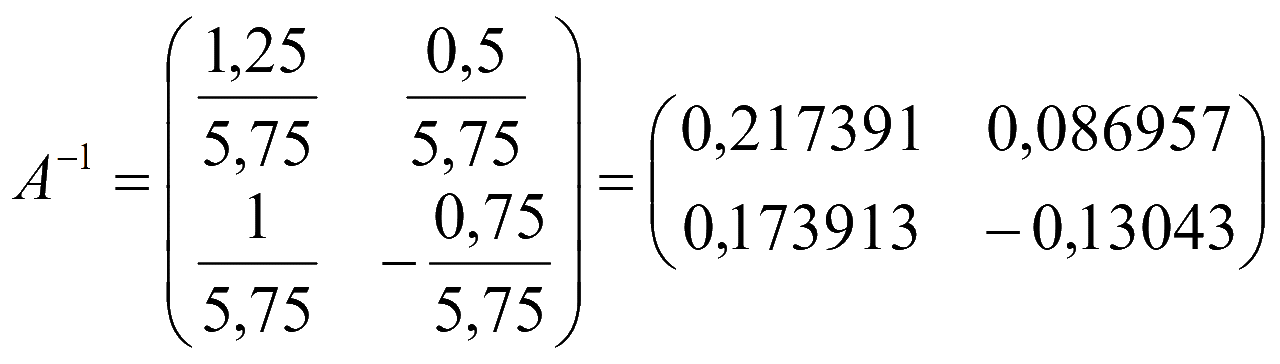
Метод Гаусса - Жордана - 3-й способ решения системы уравнений

Если справа к матрице системы приписать столбец свободных членов (получим расширенную матрицу), то в результате элементарных преобразований на месте матрицы системы необходимо получить единичную матрицу, тогда справа получим матрицу столбец A^-1B, которая равна матрице — столбцу решений системы X

[A|B] → [E|A^-1B] → [E|X]

Расширенная матрица системы

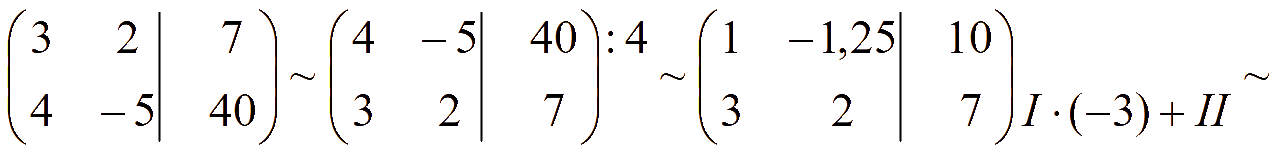
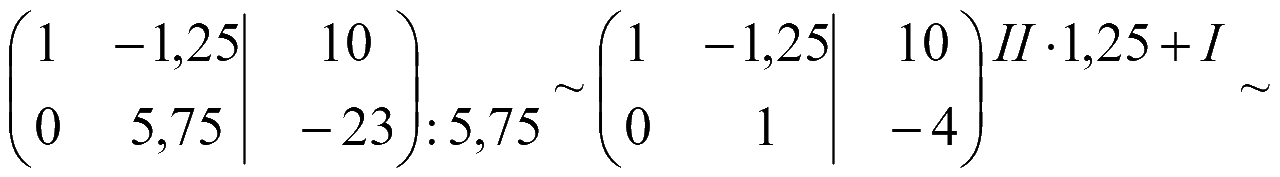
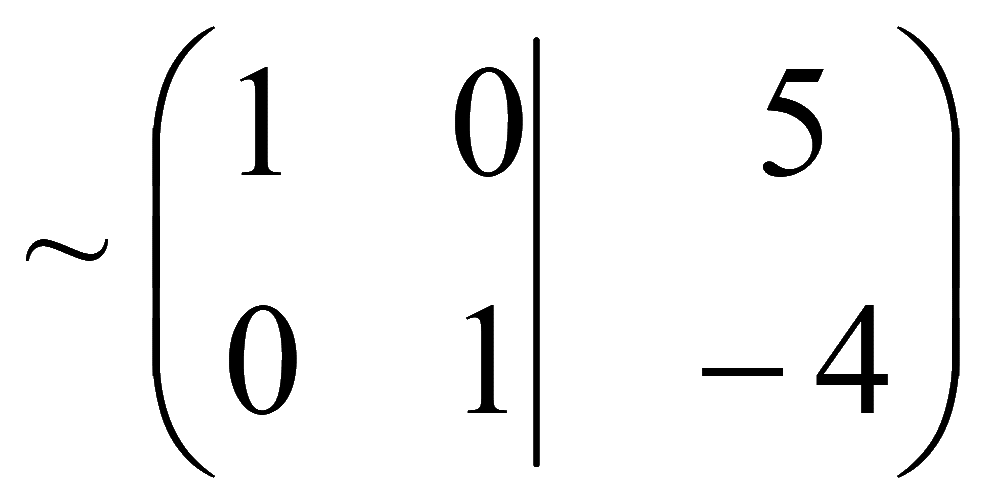
Полученной матрице соответствует система уравнений

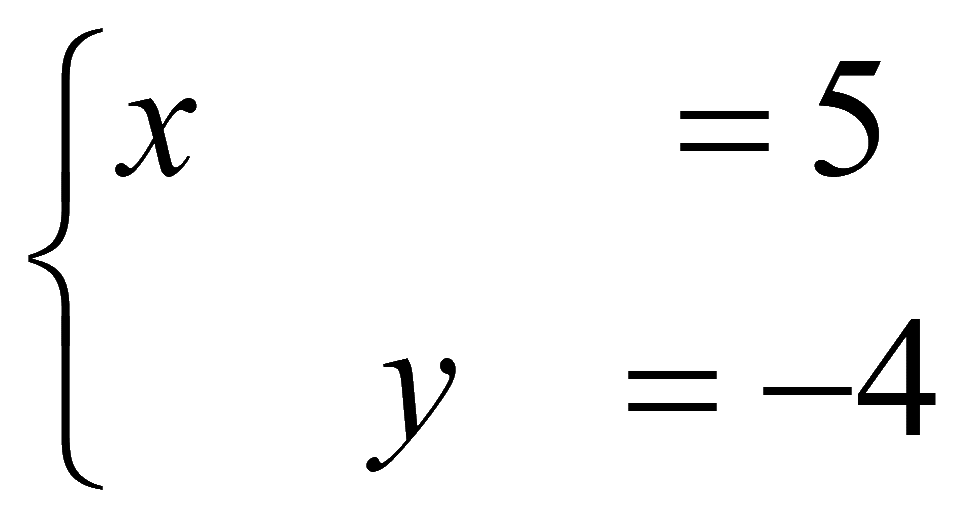
Матрица-столбец решений системы

10 Метод Крамера

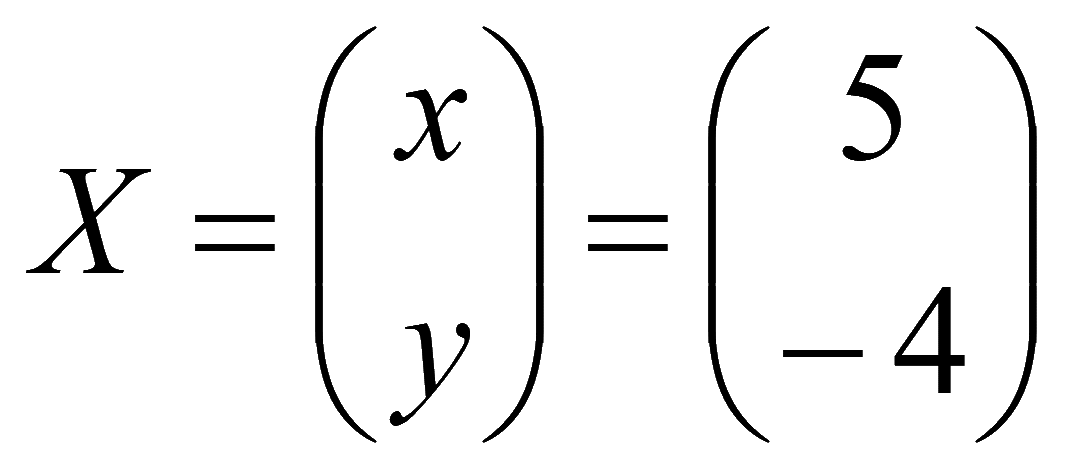
Метод Крамера заключается в следующем. Если определитель системы не равен нулю

,

то первая неизвестная

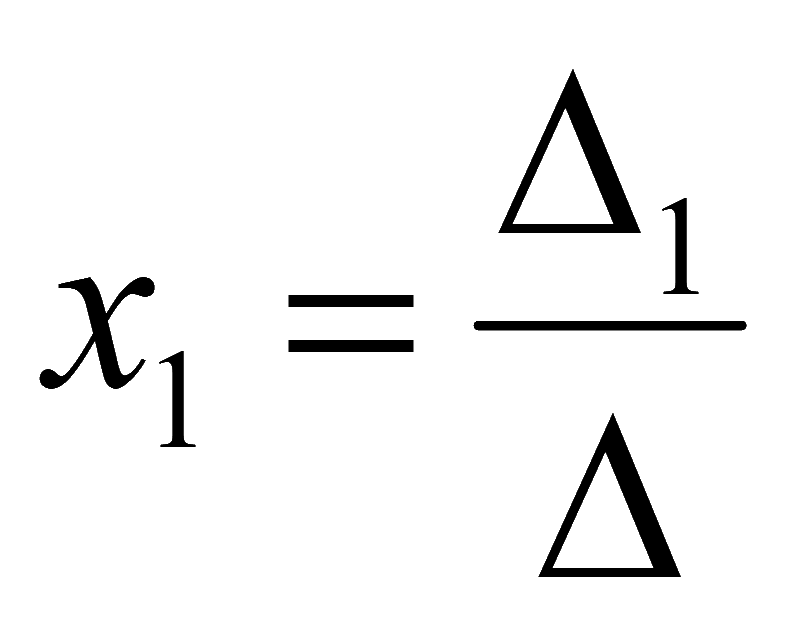
2-ая неизвестная

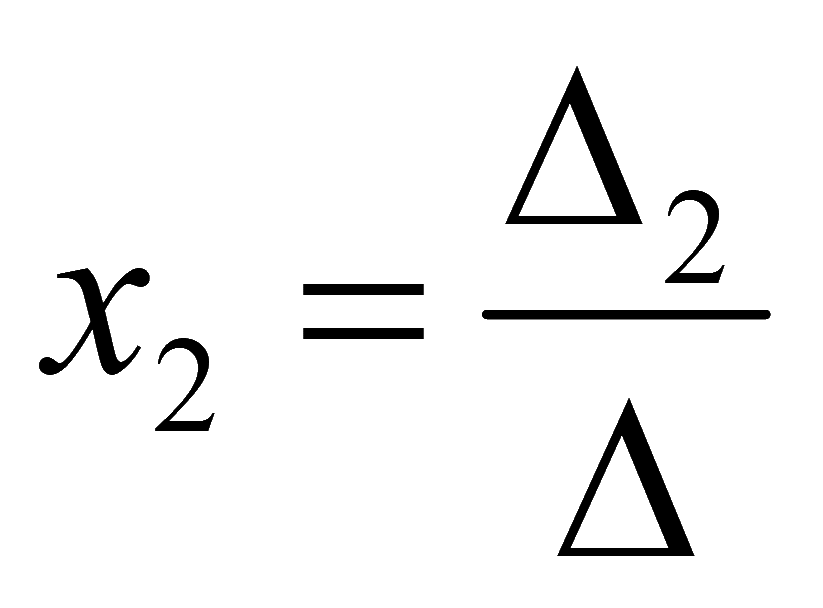
3-я неизвестная

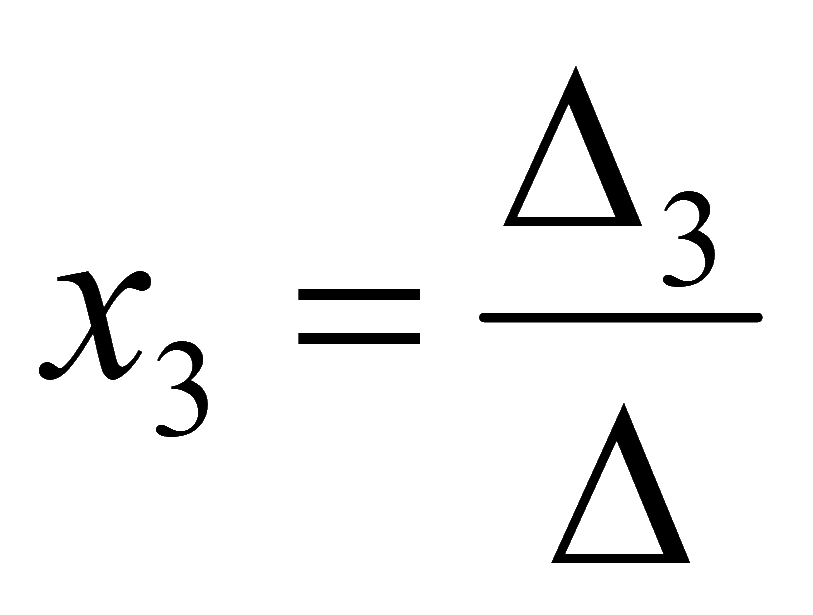
Пример. Решить систему методом Крамера

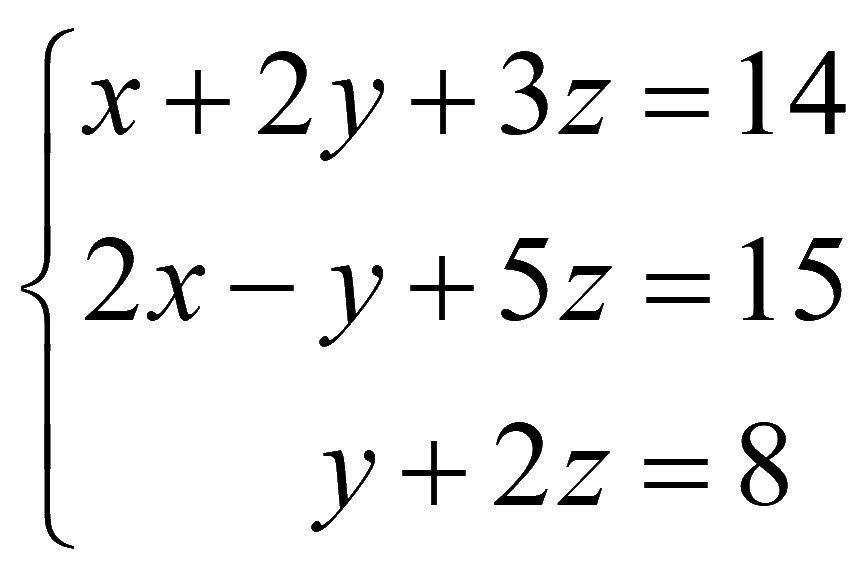
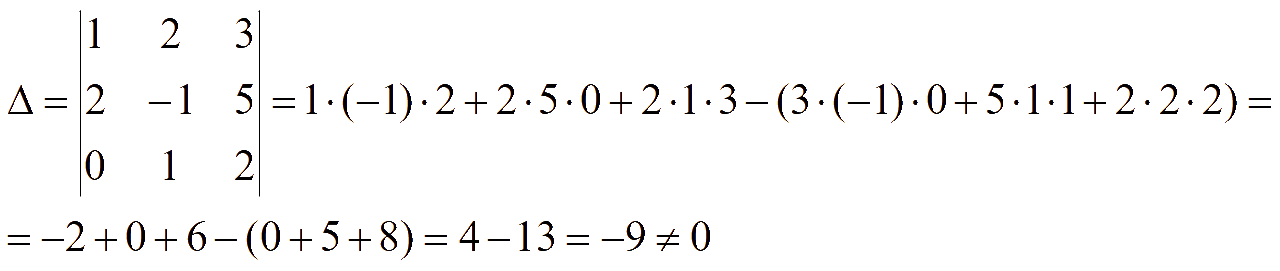
Заменим первый столбец на столбец свободных членов

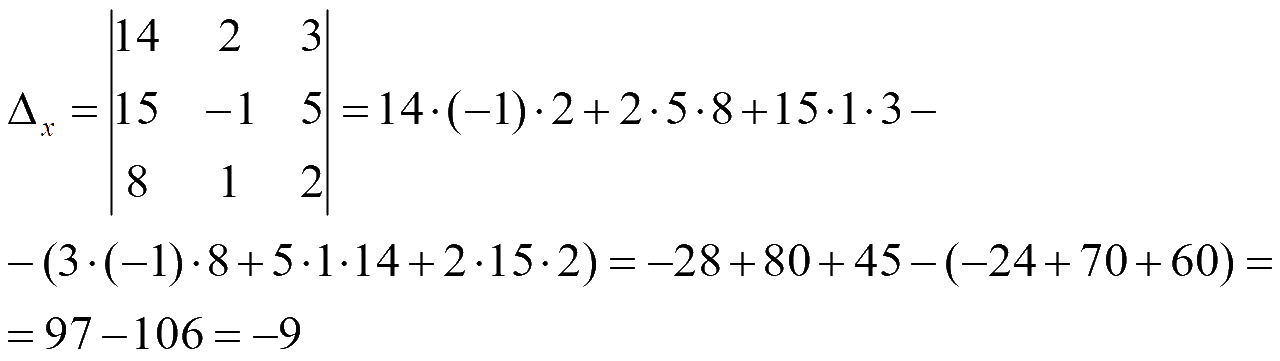
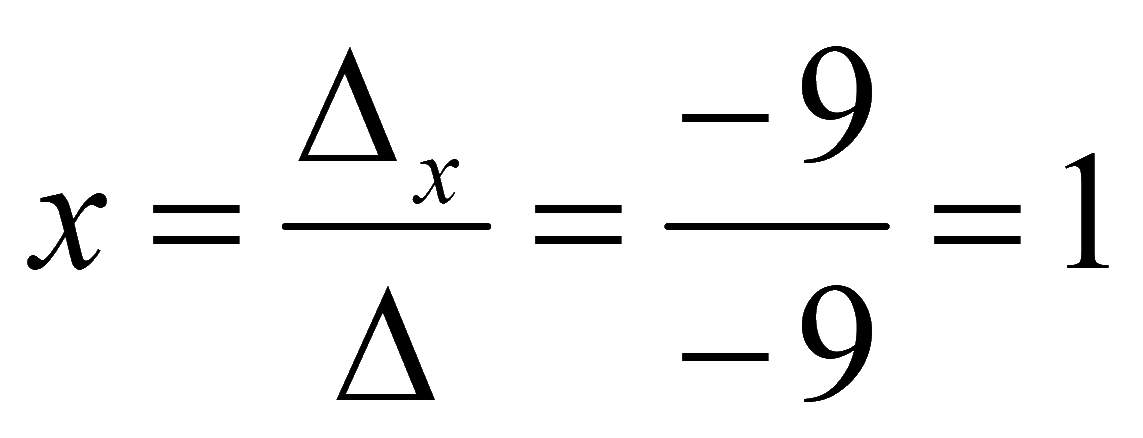
Заменим второй столбец на столбец свободных членов

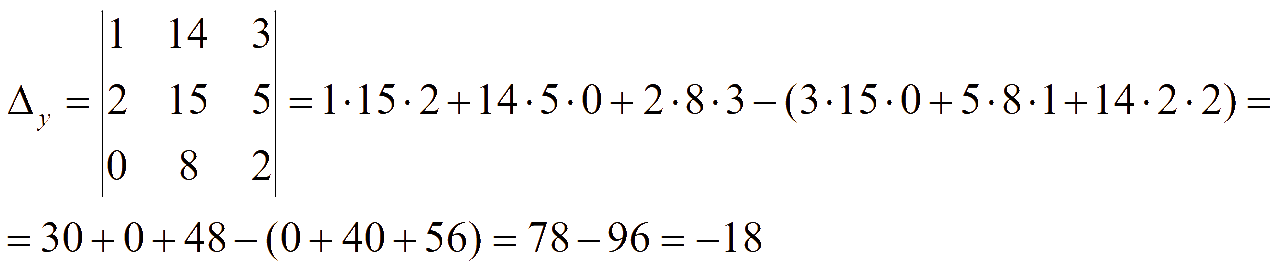
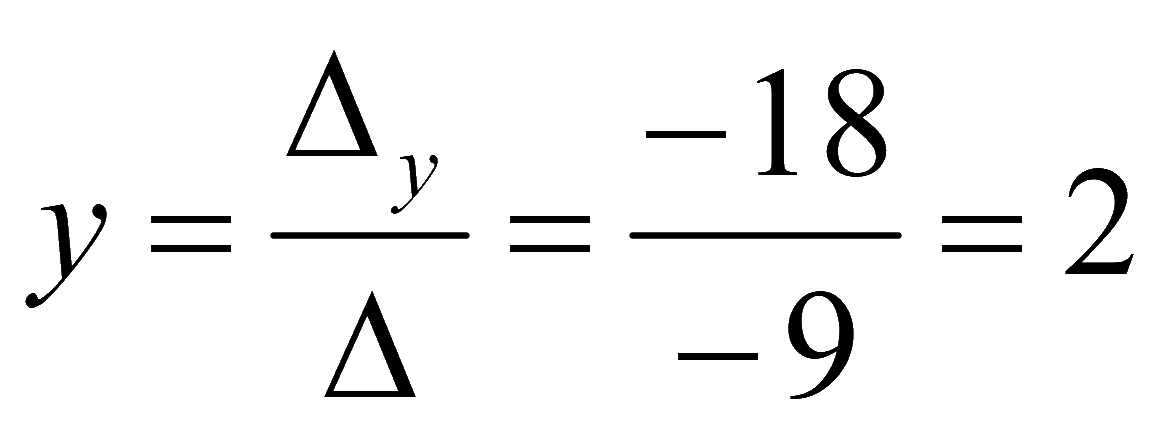
Заменим третий столбец на столбец свободных членов

11 Метод Гаусса (метод исключения неизвестных)

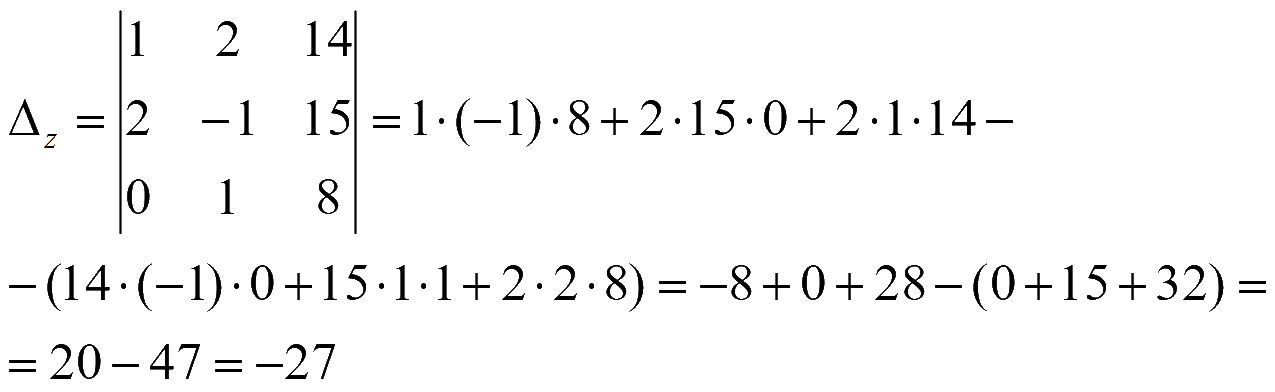
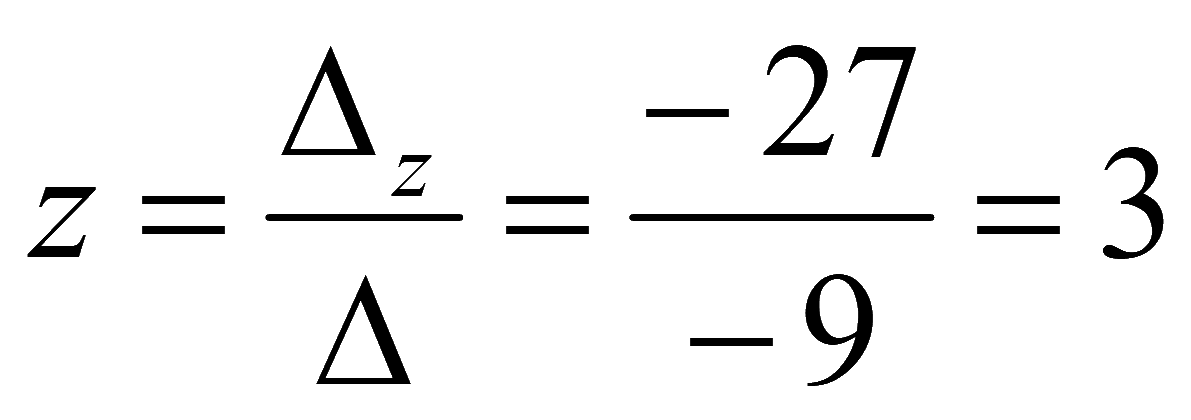
Пример. Решить систему методом Гаусса

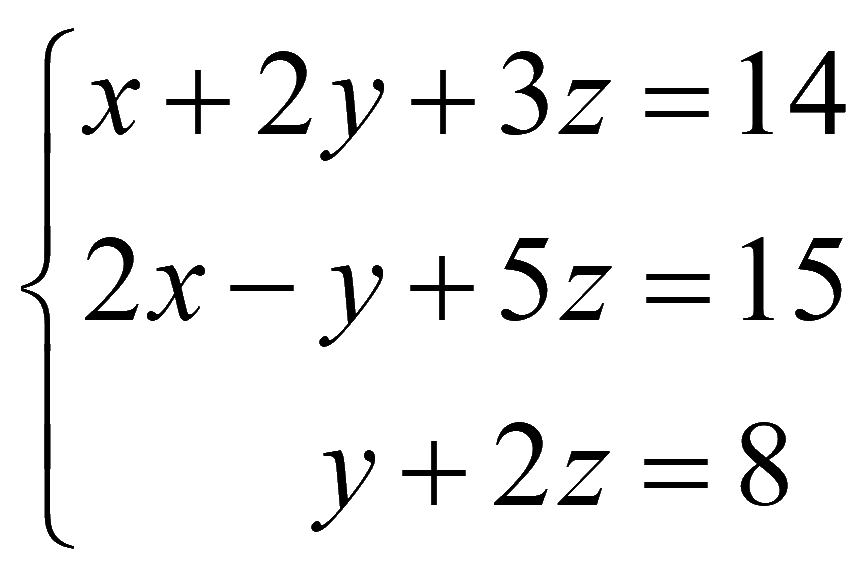
Составим расширенную матрицу и при помощи эквивалентных преобразований обнулим элементы ниже главной диагонали матрицы системы

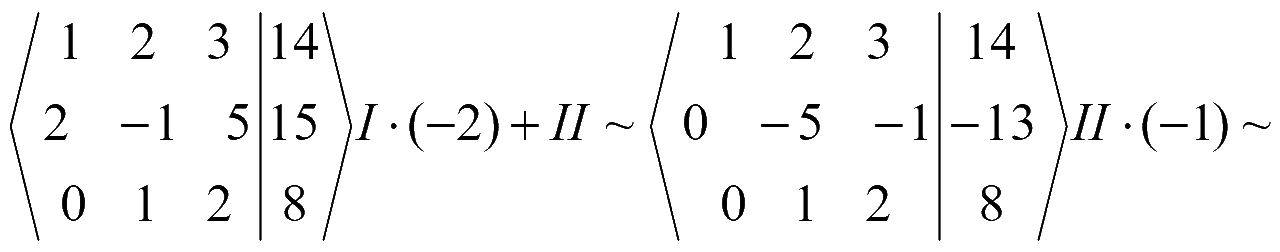
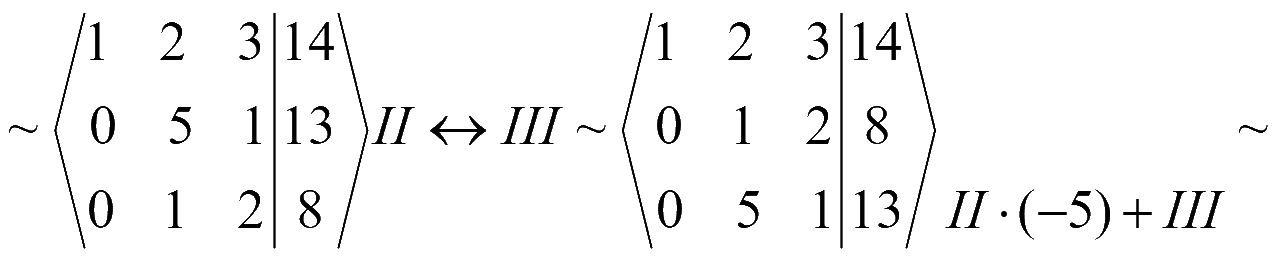
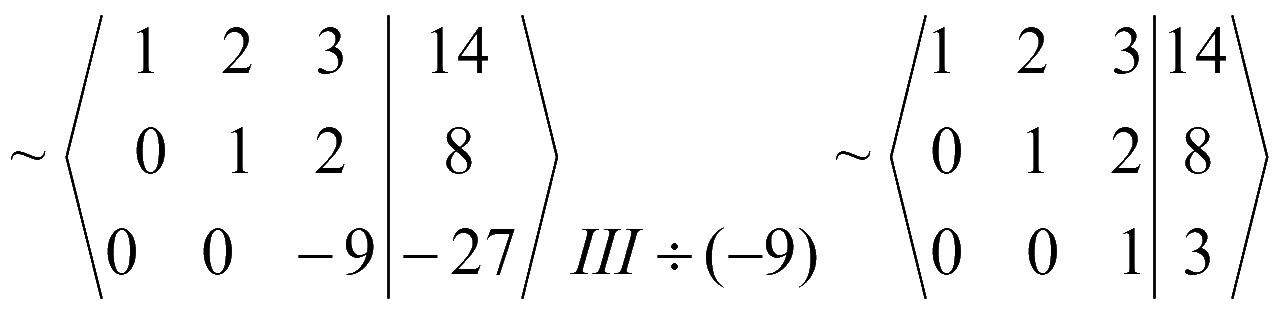
Полученной матрице соответствует система уравнений

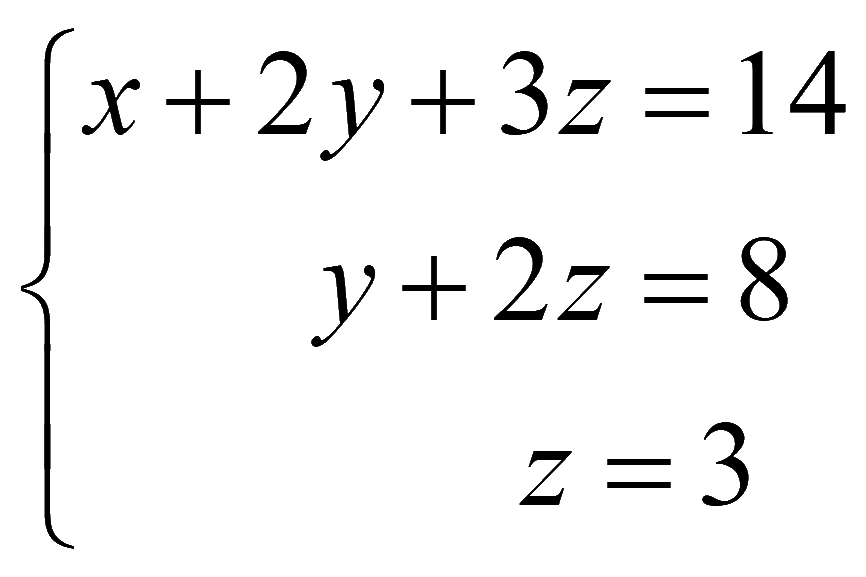
Решаем систему уравнений снизу вверх

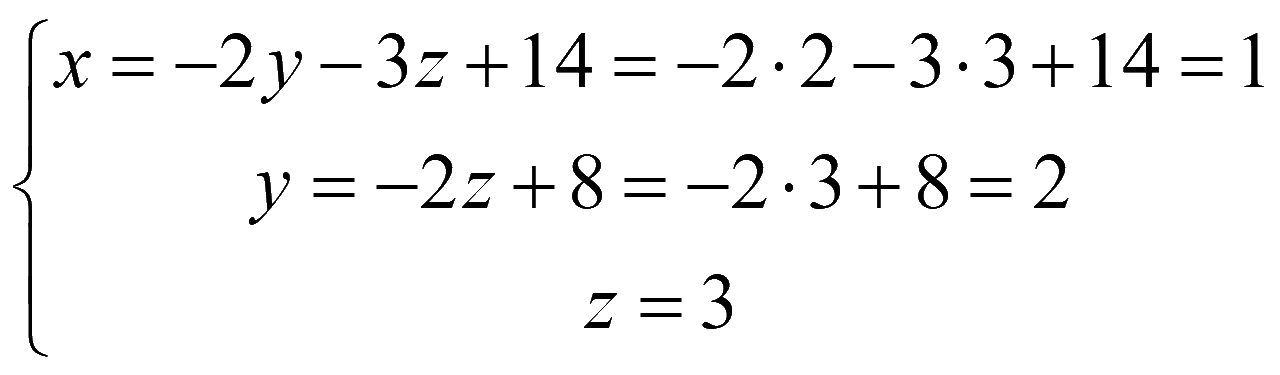
Пример. Решить систему уравнений методом Гаусса

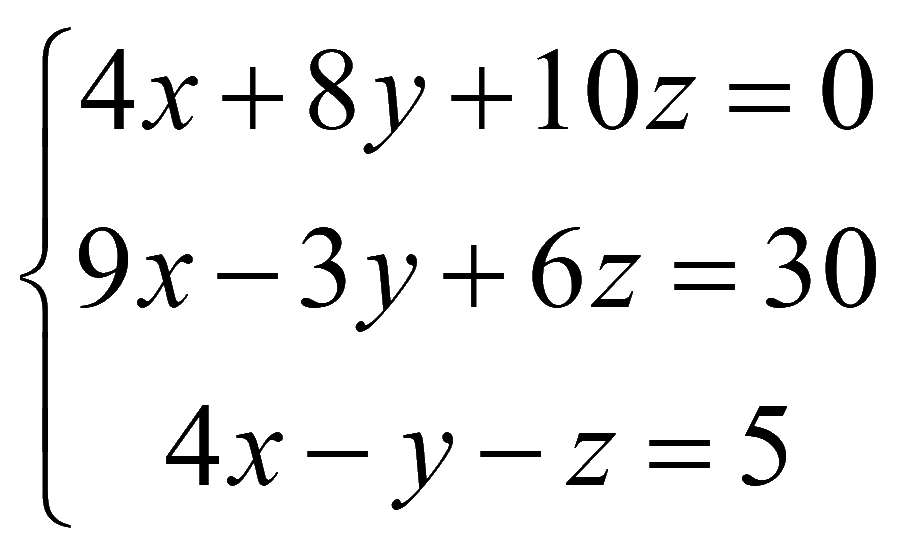
Решение

Составим расширенную матрицу и при помощи эквивалентных преобразований обнулим элементы ниже и выше главной диагонали матрицы системы (метод Гаусса - Жордана)

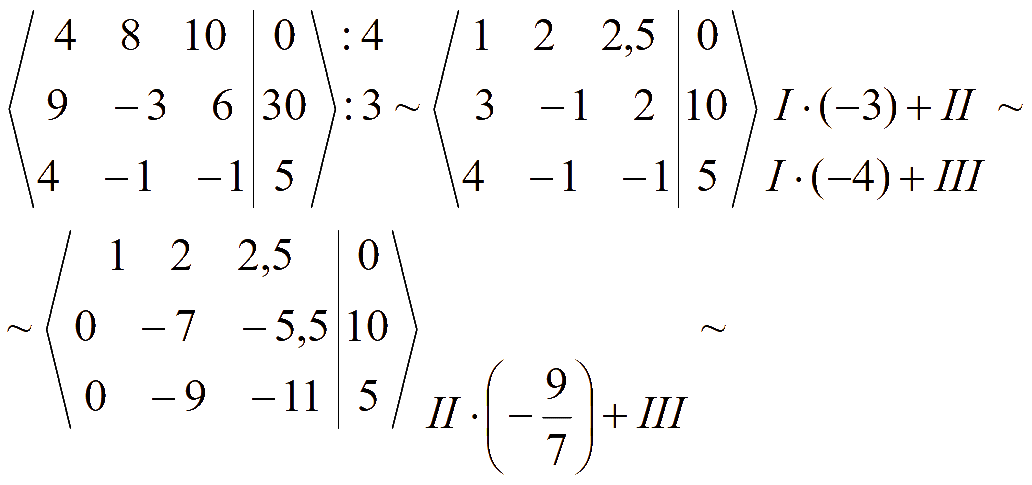
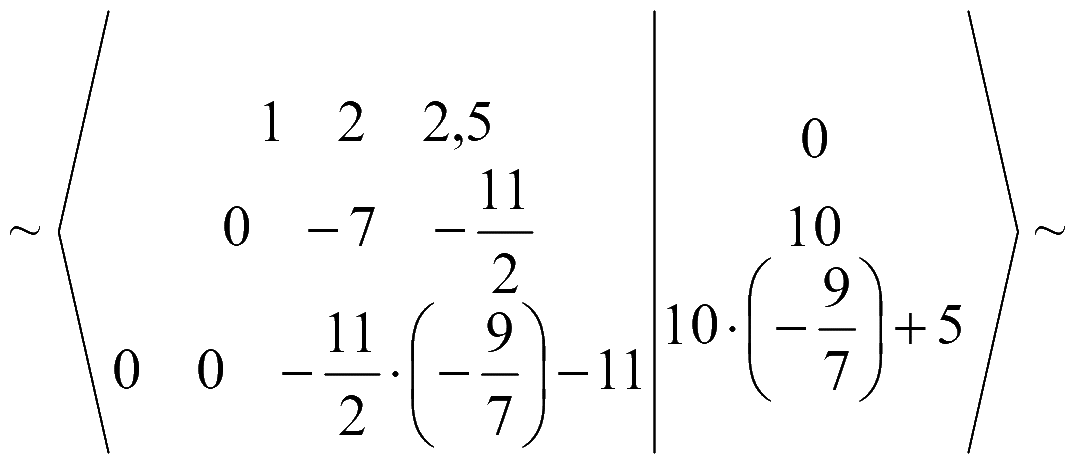
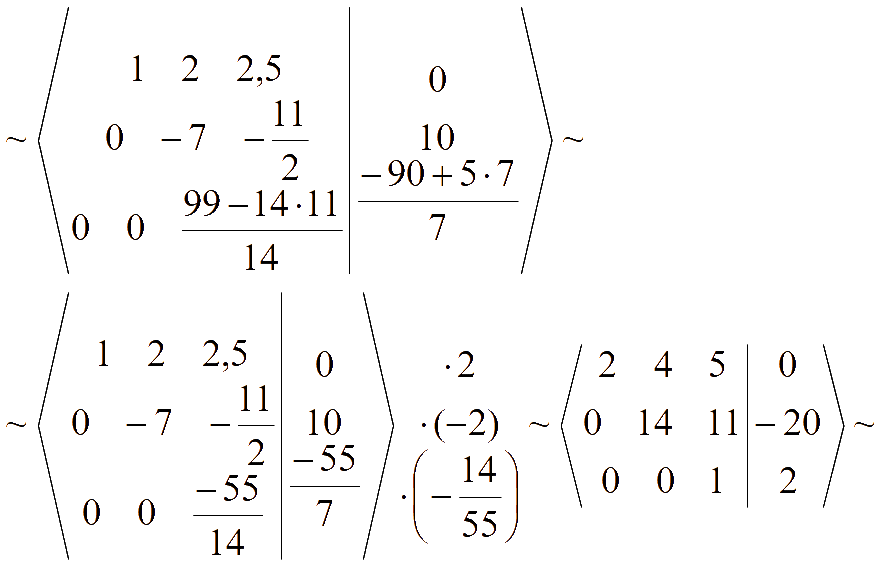
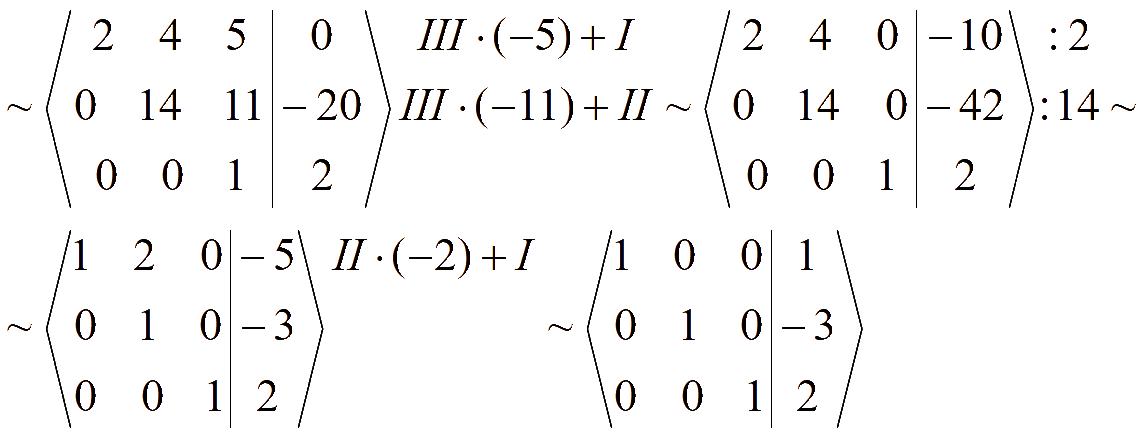
Полученной матрице соответствует система уравнений

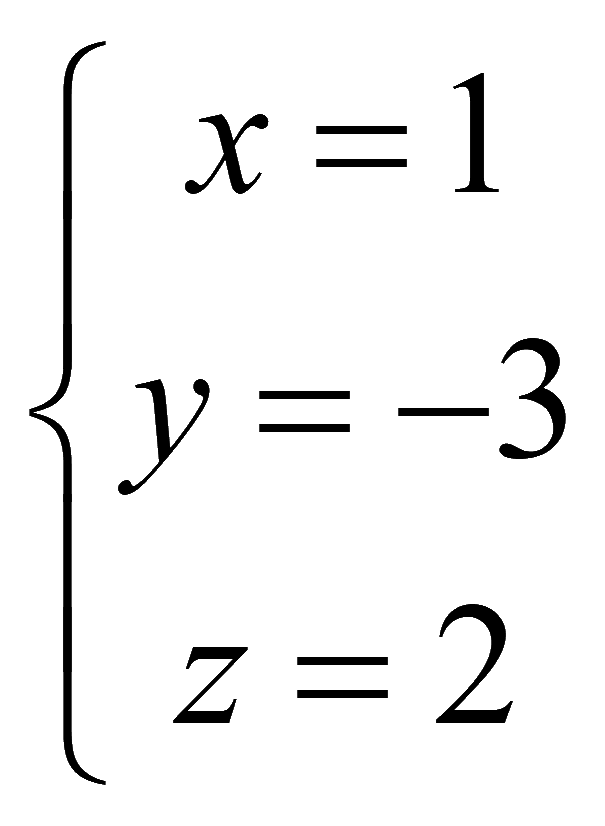
Проверка

Подставим решение в исходную систему уравнений

,

,

,

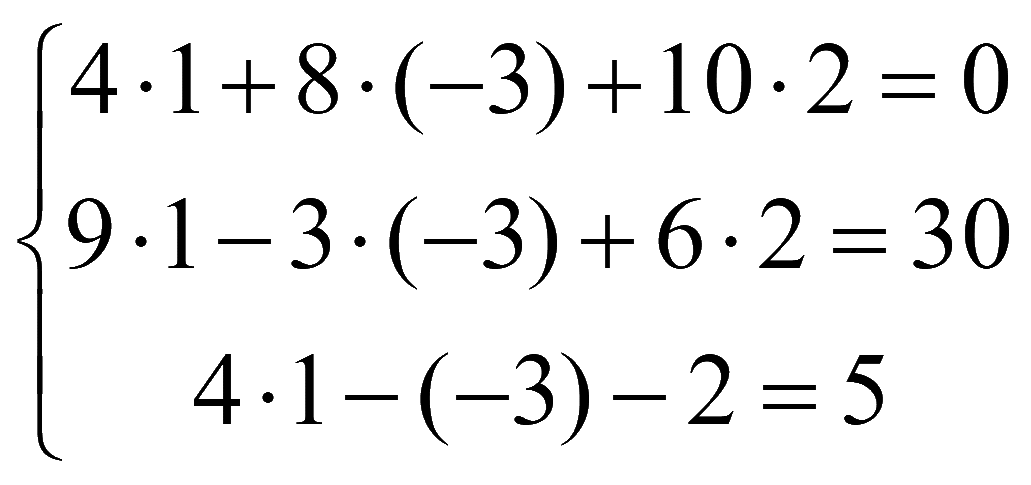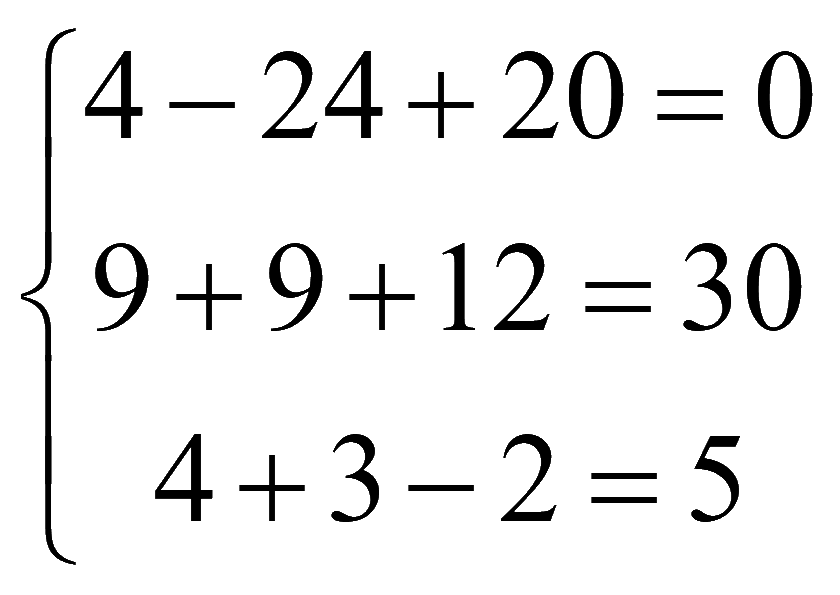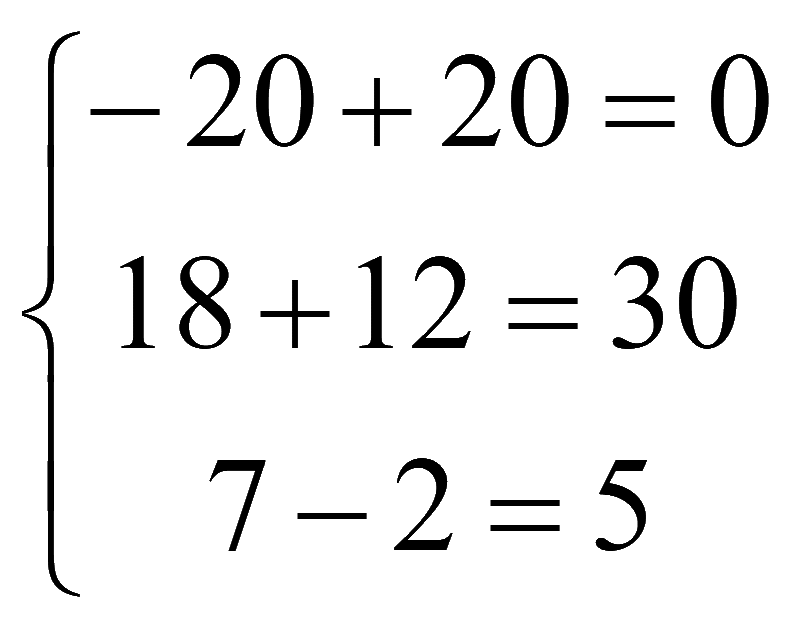верно.

12 Матричный метод

Система уравнений в матричном виде

AX = B

Если определитель матрицы не равен нулю (detA ≠ 0), то существует обратная матрица A^-1.

Матрица, умножаемая на X в матричном уравнении, перемещается в другую часть равенства в виде обратной матрицы умножаемой на B в решении матричного уравнения. Решение системы уравнений в матричном виде

X = A^-1B.

Если система уравнений в матричном виде

XA = B,

то решение системы уравнений в матричном виде. X, умноженный на матрицу в матричном уравнении равен B, умноженной на обратную матрицу в решении матричного уравнения:

X = BA^-1

Если система уравнений в матричном виде содержит матрицы A и C

AXC = B,

то решение системы уравнений в матричном виде

X = A^-1BC^-1

Положение матрицы в матричном уравнении по отношению к X (до или после) сохраняется применительно к положению обратной матрицы по отношению к B (до или после).

Пример 1.4.29 [1]. Решить матричное уравнение

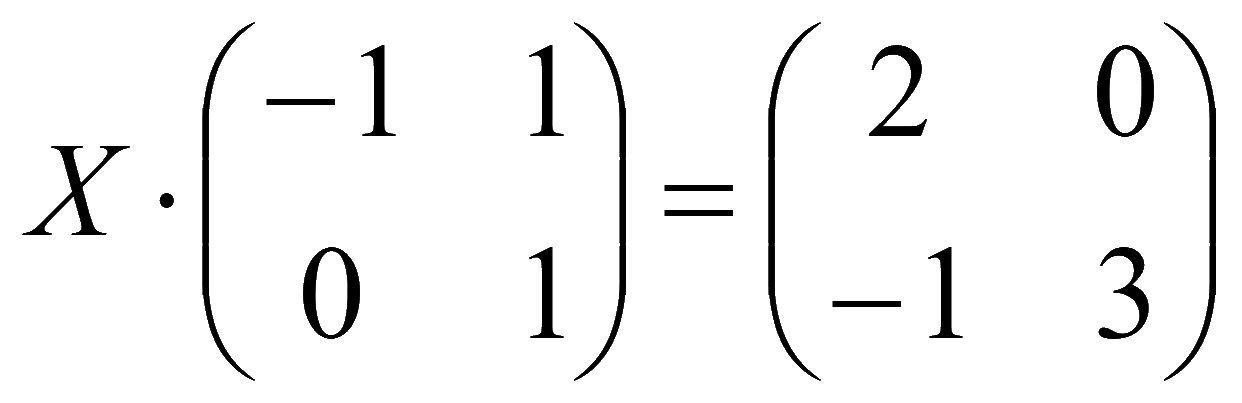
Решение

Матрицы

;

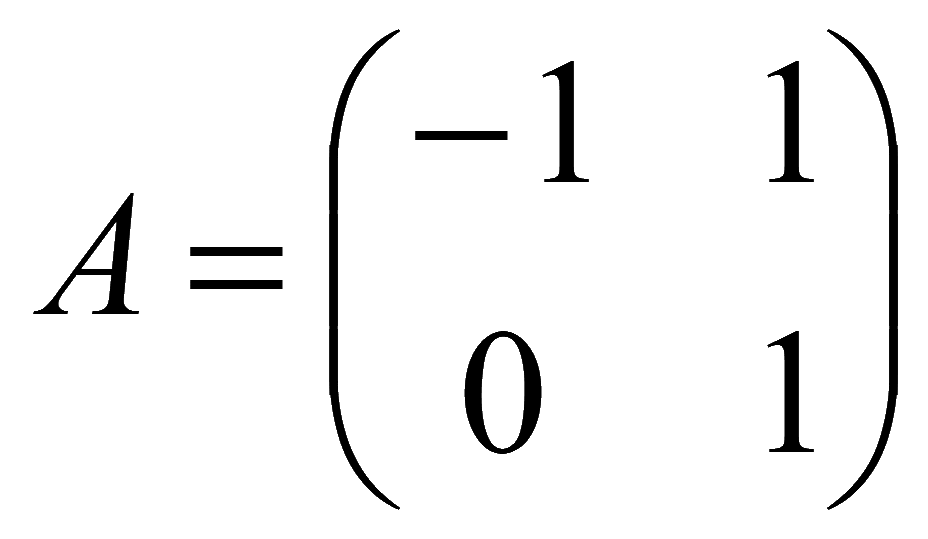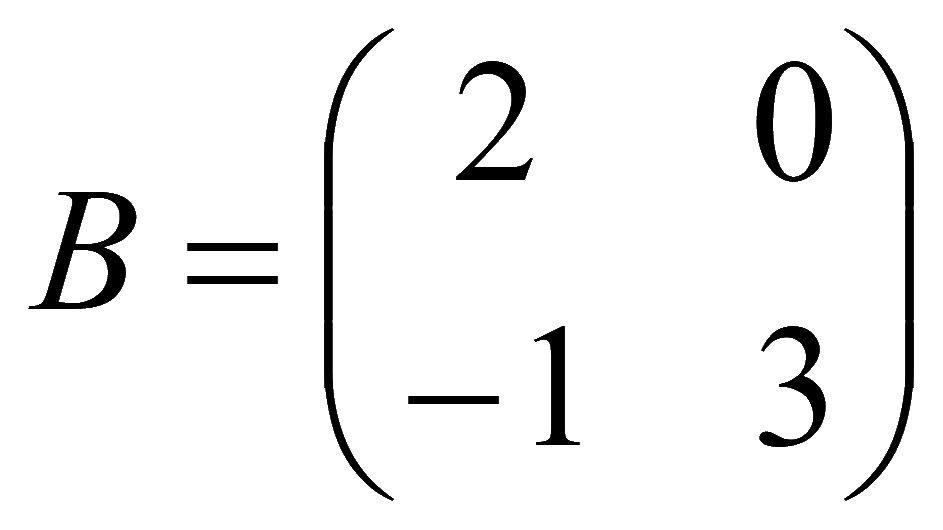
Решение матричного уравнения XA = B в виде

X = BA^-1.

Обратную матрицу найдем методом Жордана. Для этого справа от матрицы системы припишем единичную матрицу, затем при помощи элементарных преобразований получим слева единичную матрицу, тогда справа получим обратную матрицу

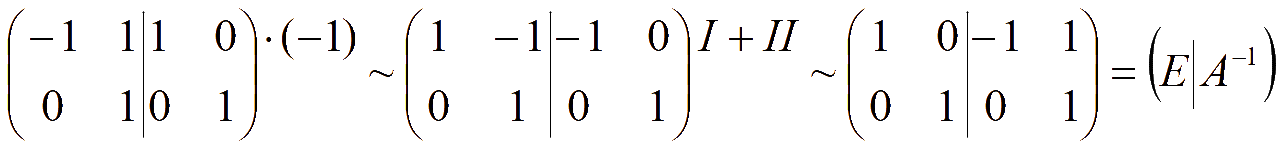
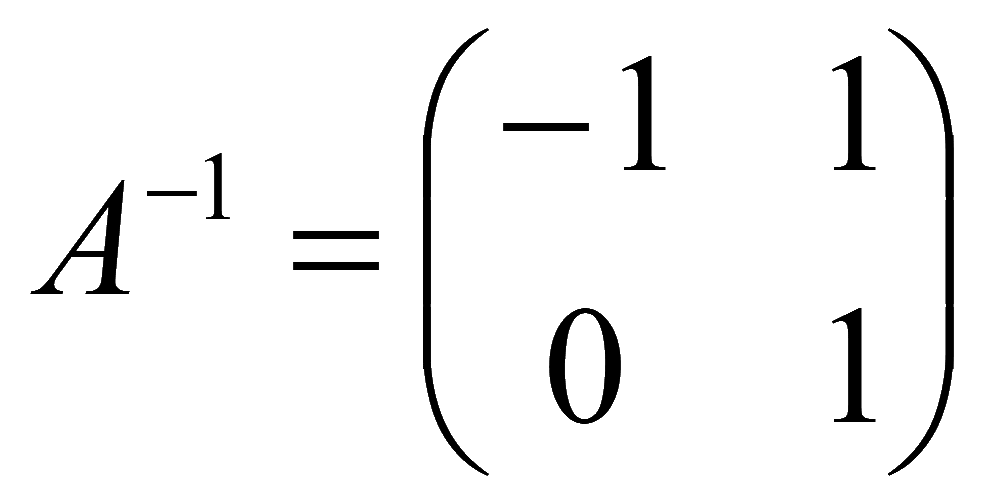
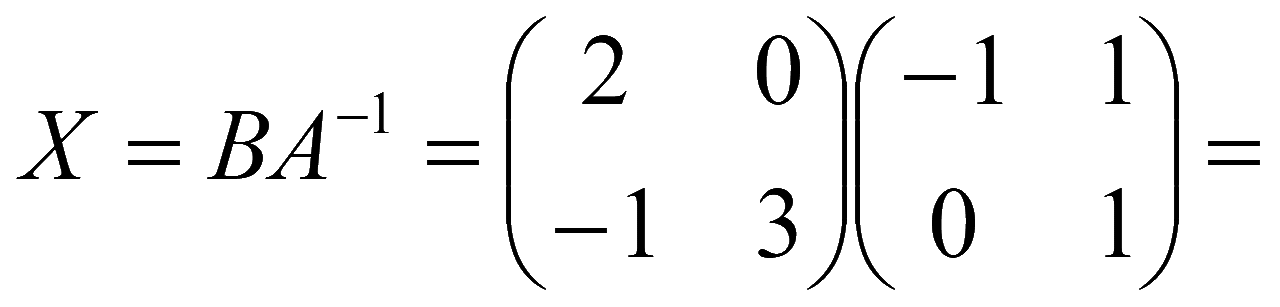
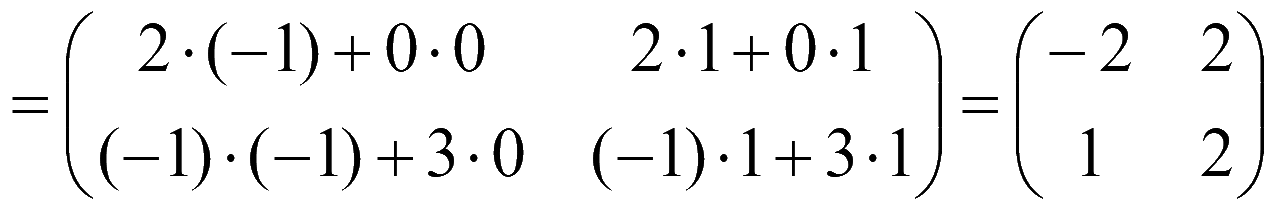
Черновик

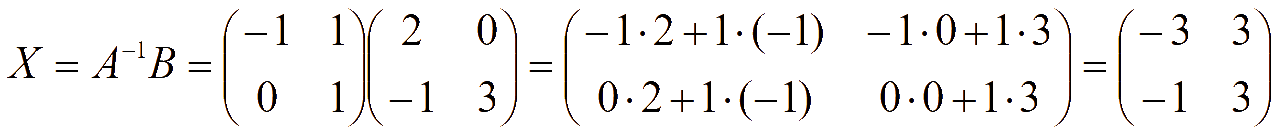
Пример. Решить систему матричным методом

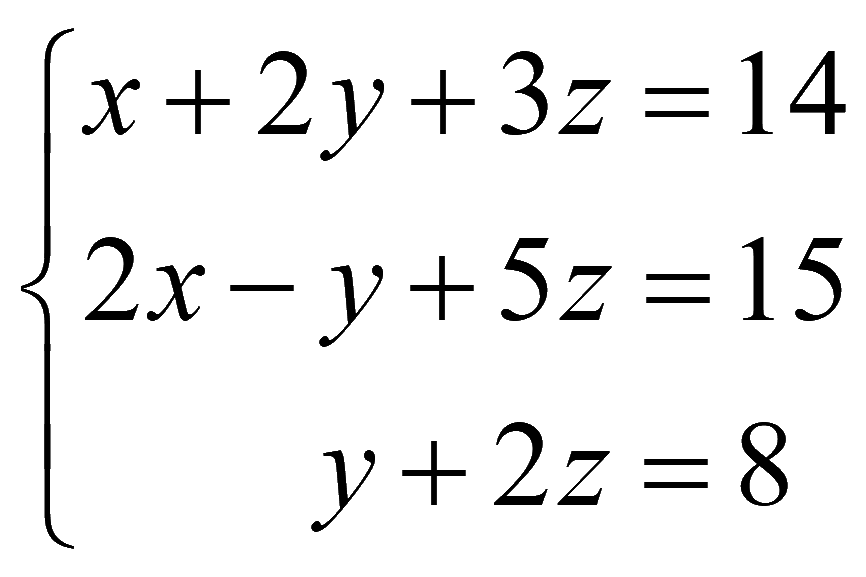
Матрица системы уравнений составляется из коэффициентов при неизвестных

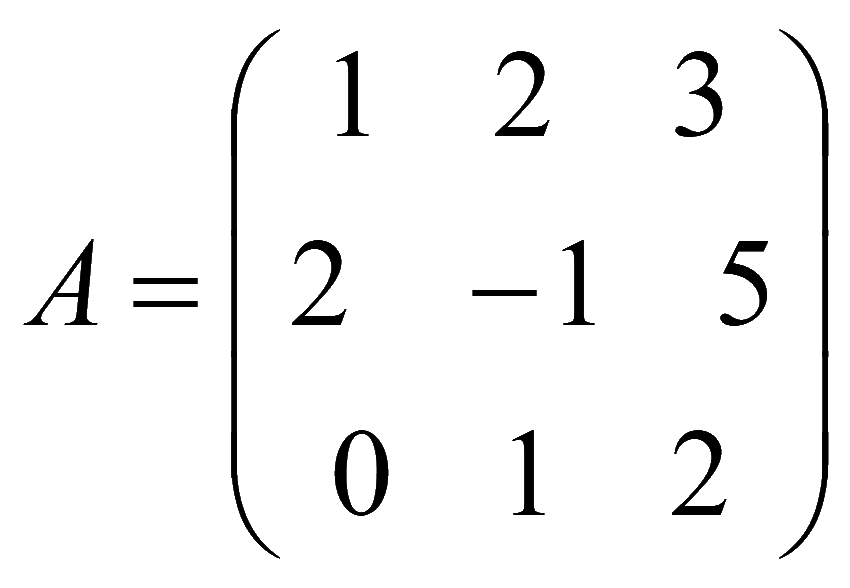
Вектор-столбец неизвестных

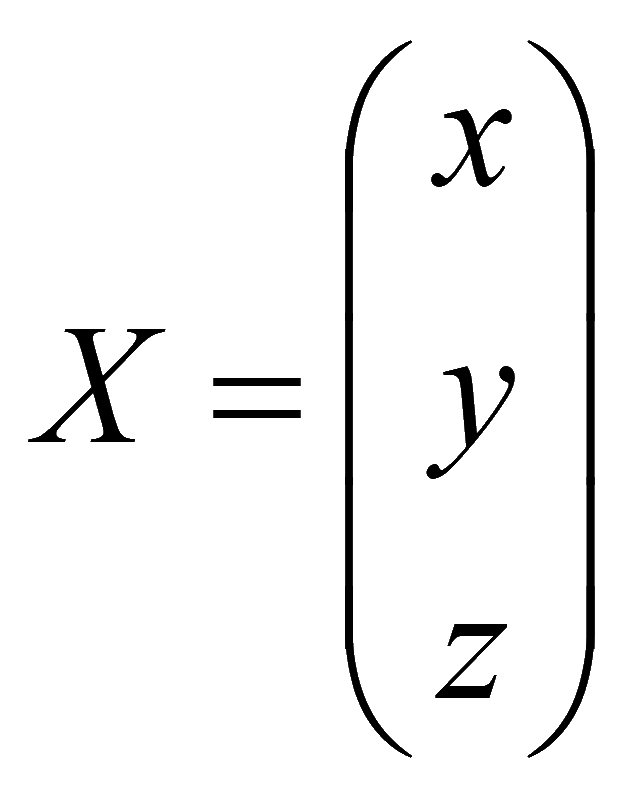
Вектор-столбец свободных членов

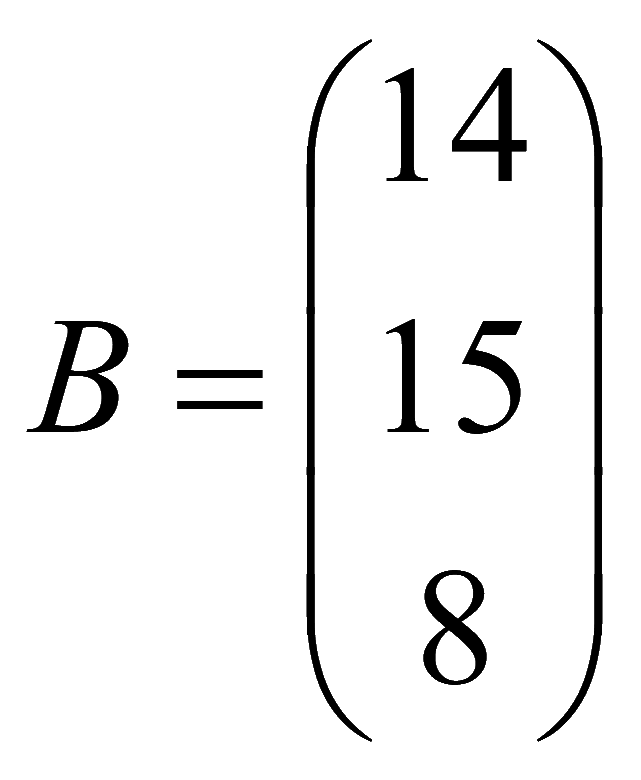
Система уравнений (1) в матричном виде

AX = B

Если определитель матрицы не равен нулю (detA ≠ 0), то существует обратная матрица A^-1. Решение системы уравнений в матричном виде

X = A^-1B.

Определитель матрицы системы уравнений

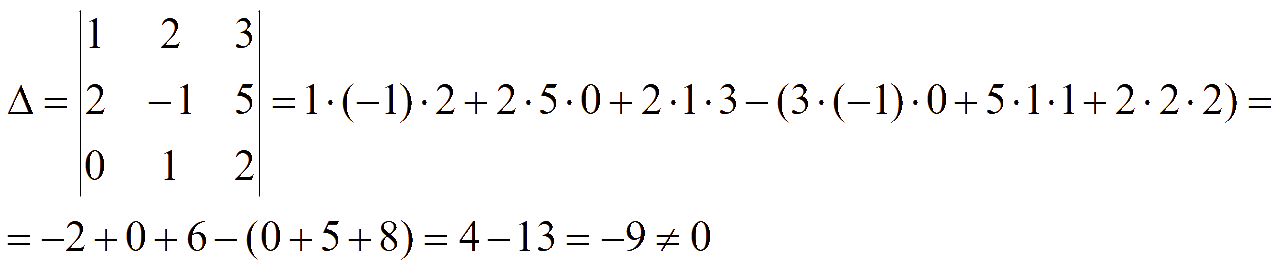
Алгебраические дополнения элементов матрицы

,

,

,

,

...

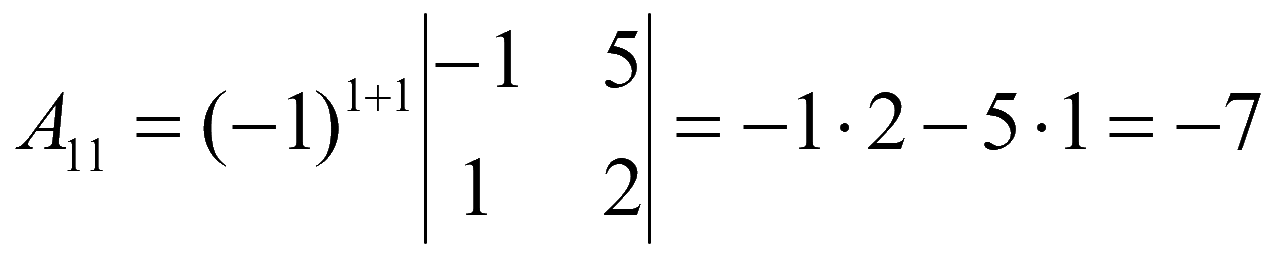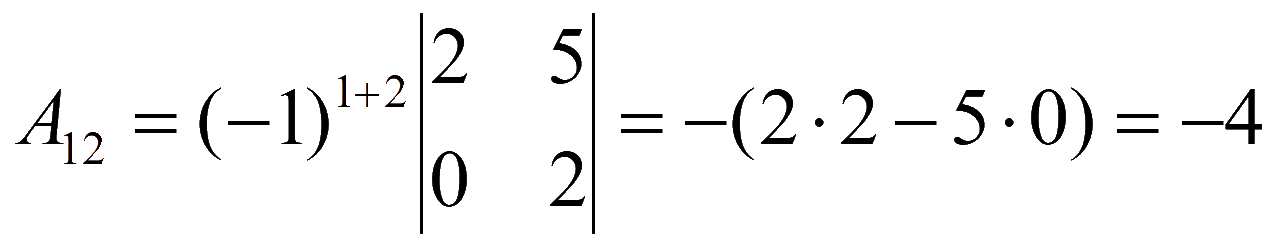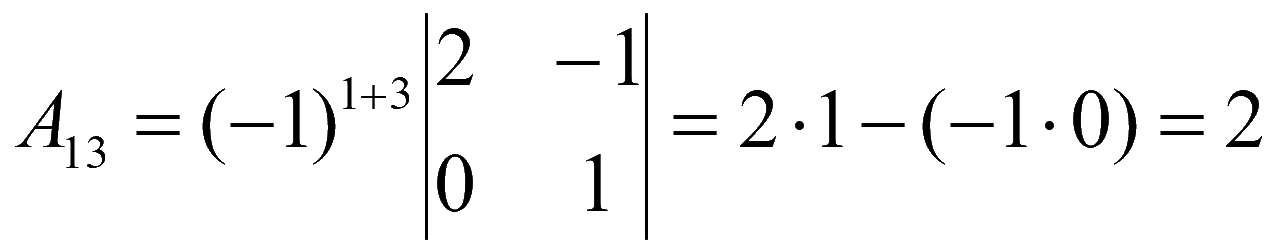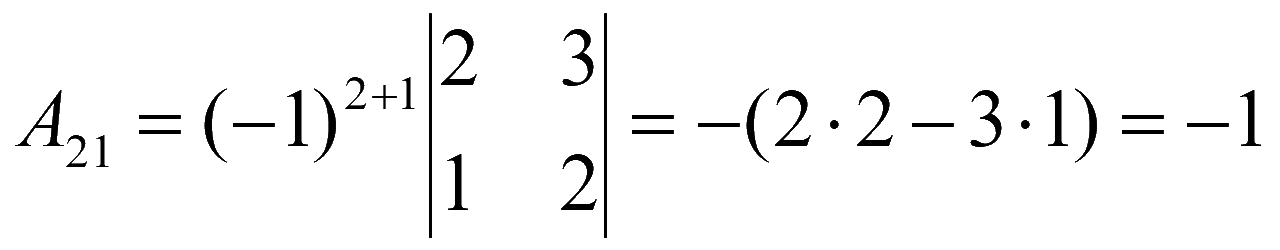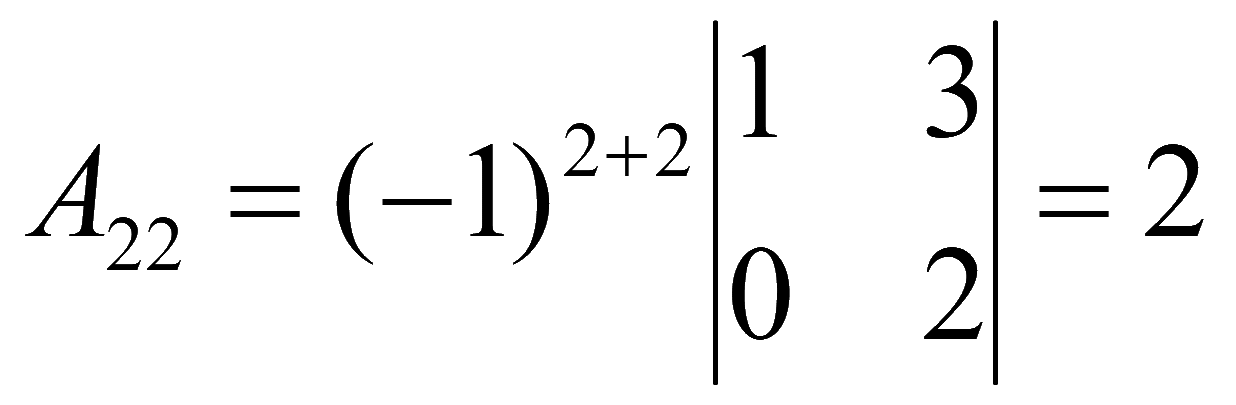
Находим обратную матрицу

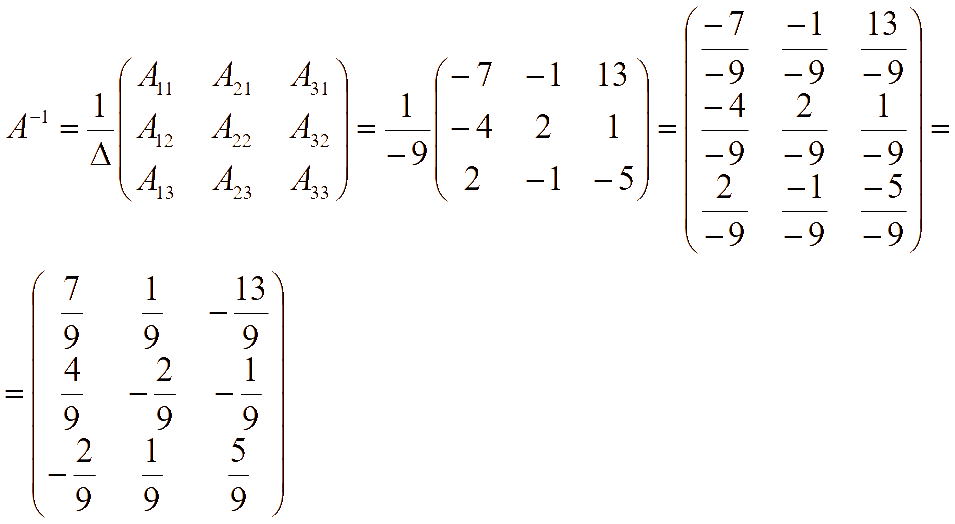
Решение системы

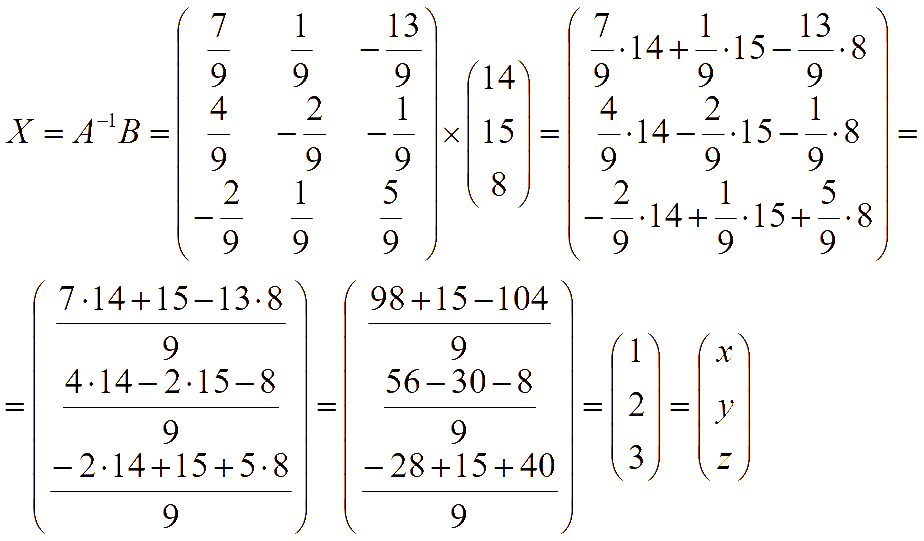
Пример. Решить методом Крамера и методом обратной матрицы

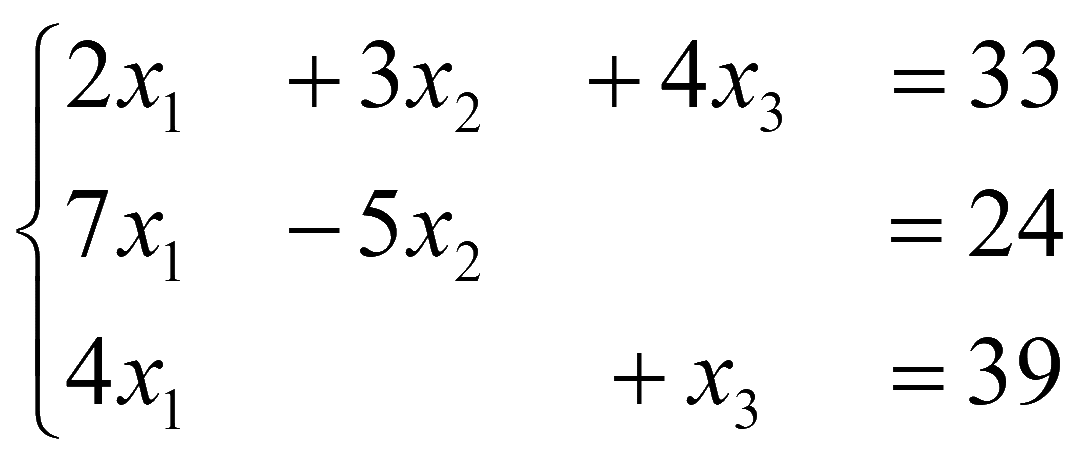
Решение

Метод Крамера

Найдем определитель матрицы системы

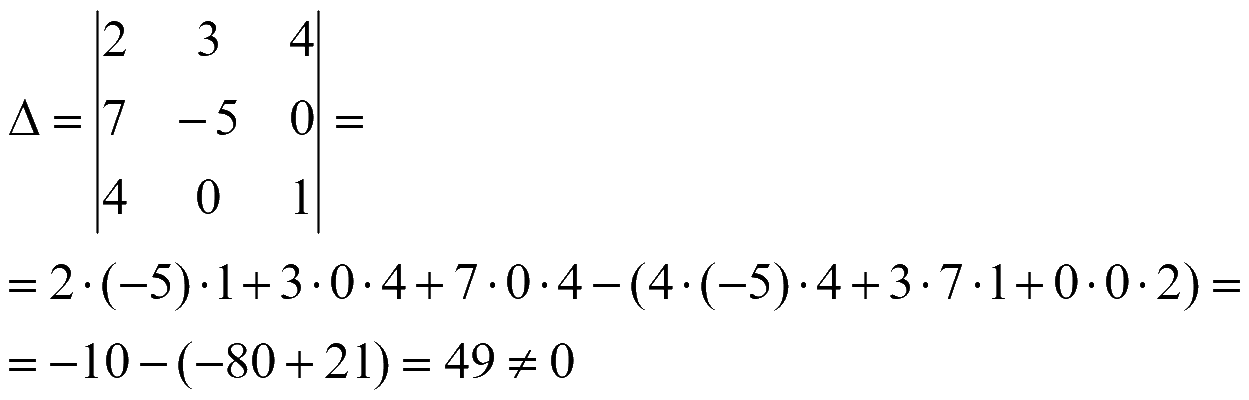
Заменим первый столбец на столбец свободных членов и найдем определитель

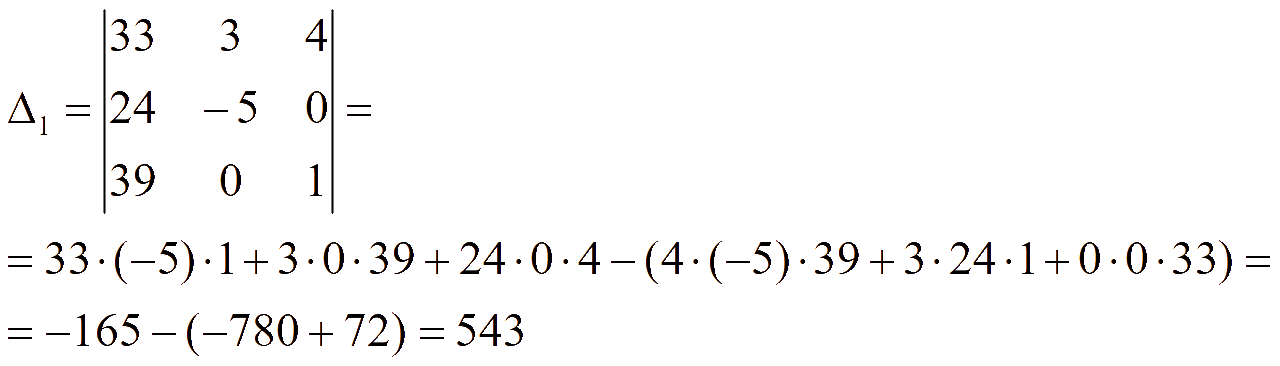
Заменим второй столбец на столбец свободных членов и найдем определитель

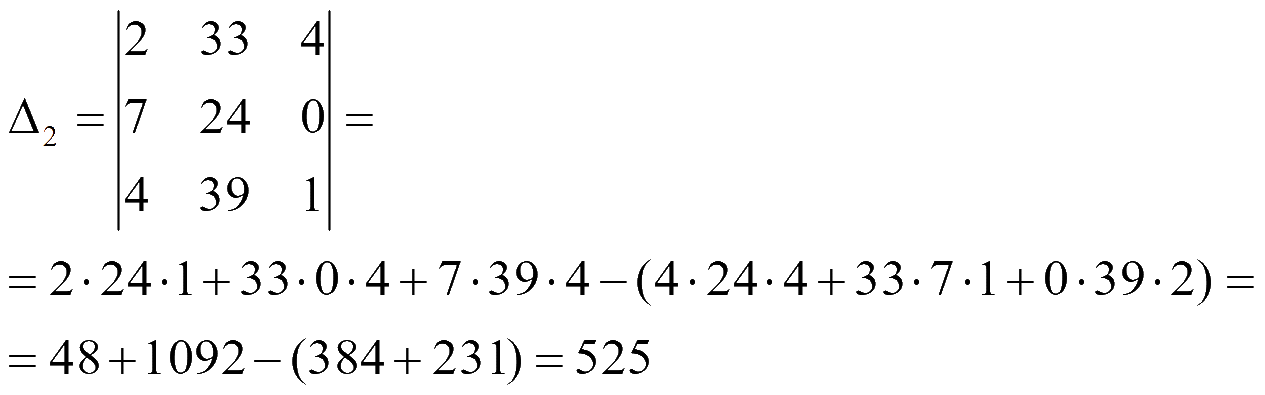
Заменим третий столбец на столбец свободных членов и найдем определитель

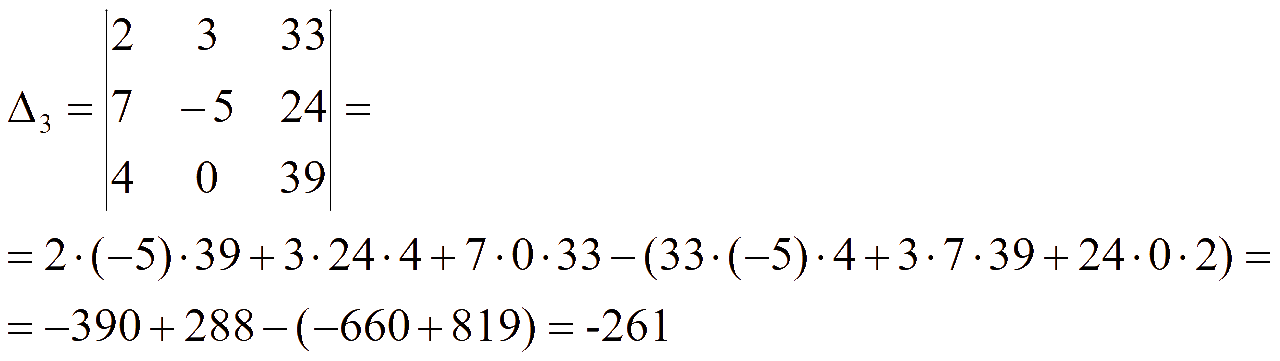
Решение системы уравнений

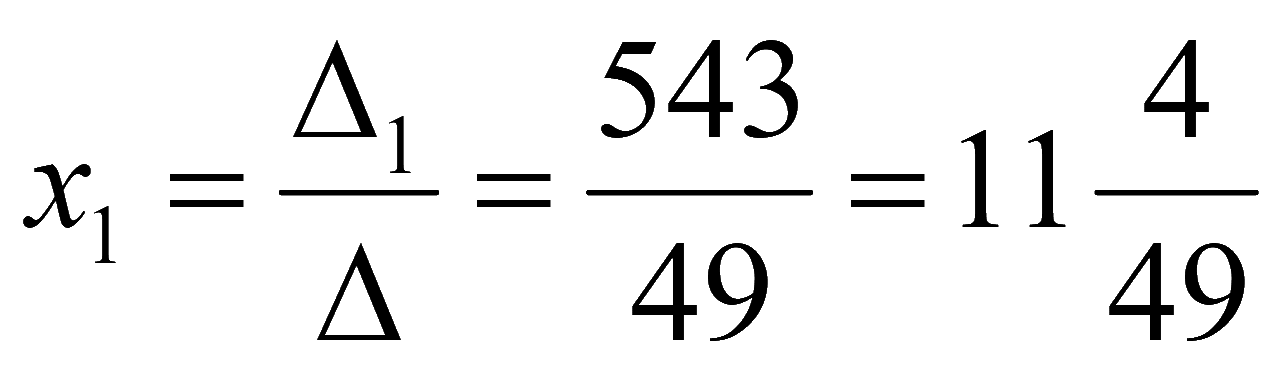
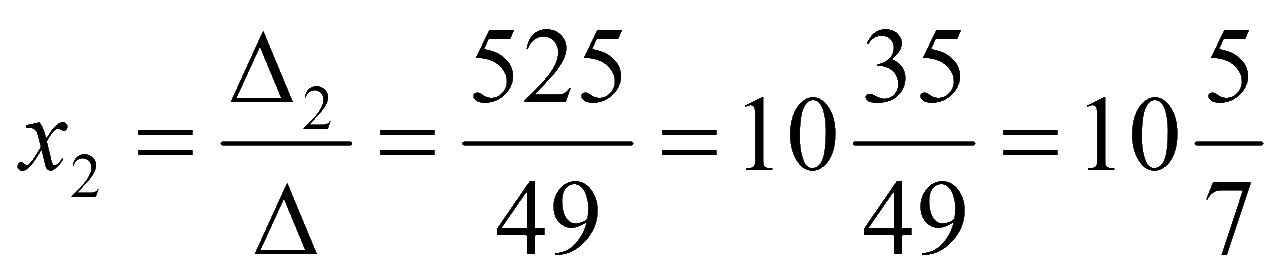
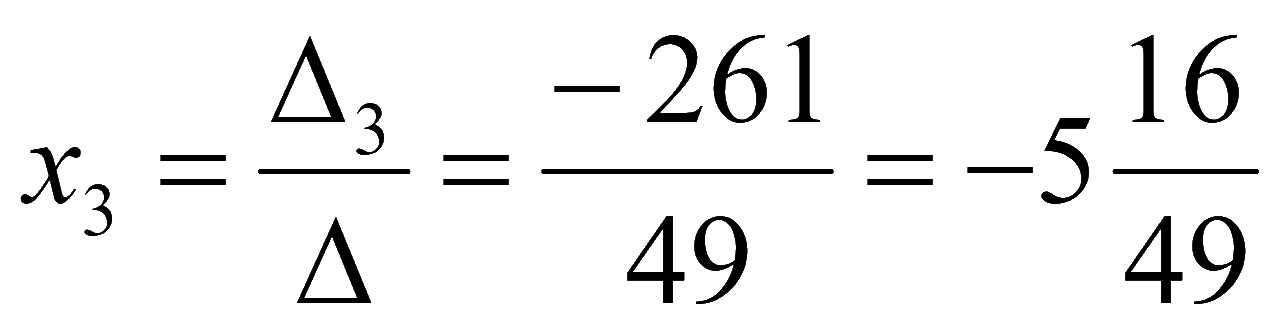
Метод обратной матрицы

Матрица системы уравнений

,

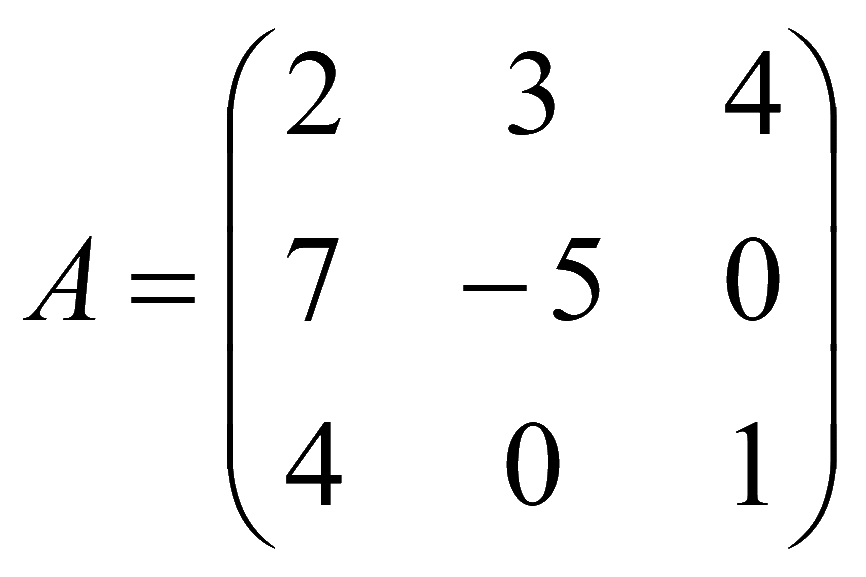вектор-столбец неизвестных

,

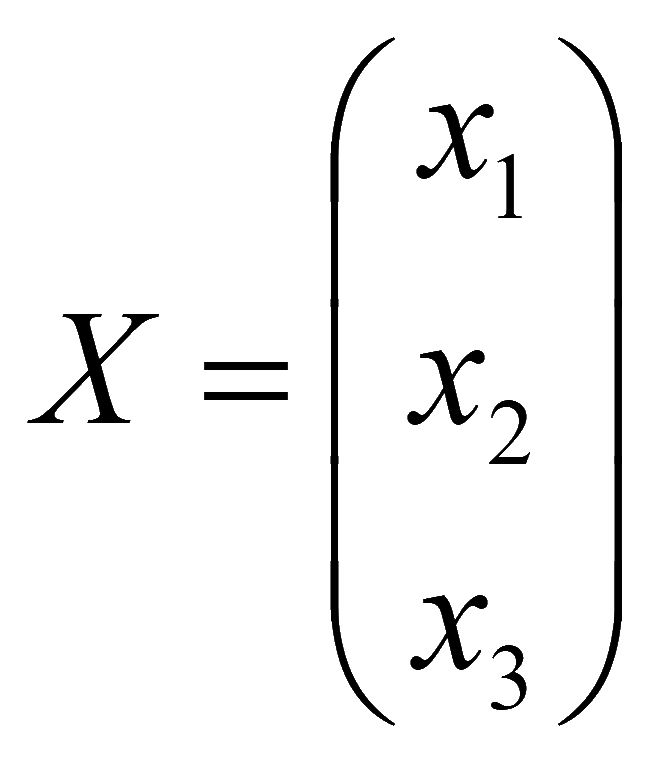вектор-столбец свободных членов

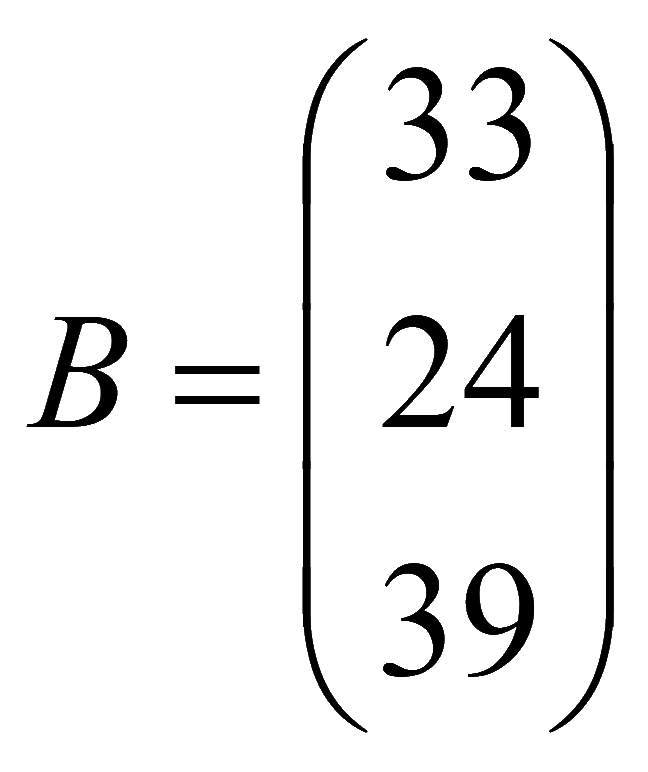
Систему уравнений можно записать в виде уравнения

AX = B,

тогда решение находится из уравнения

X = A^-1B.

Найдем обратную матрицу. Сначала находим определитель матрицы системы

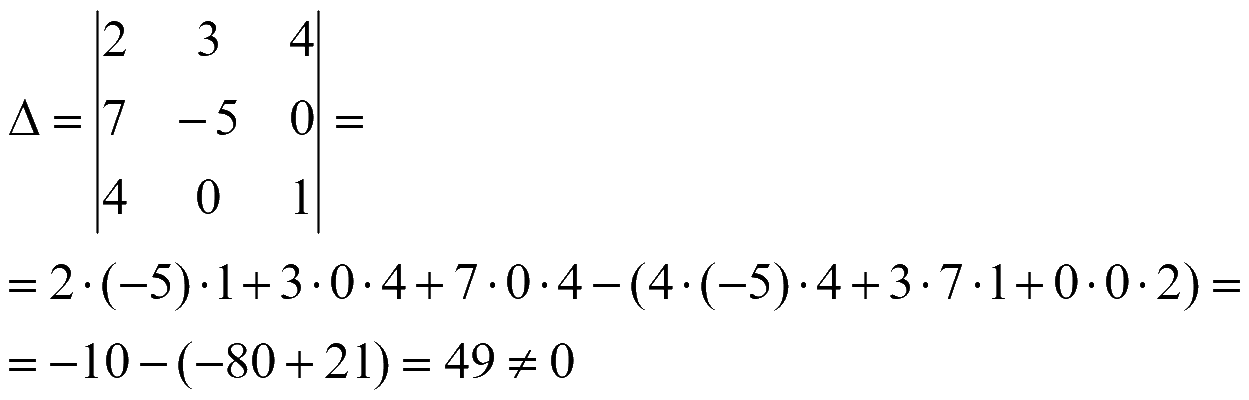
Находим алгебраические дополнения элементов матрицы системы

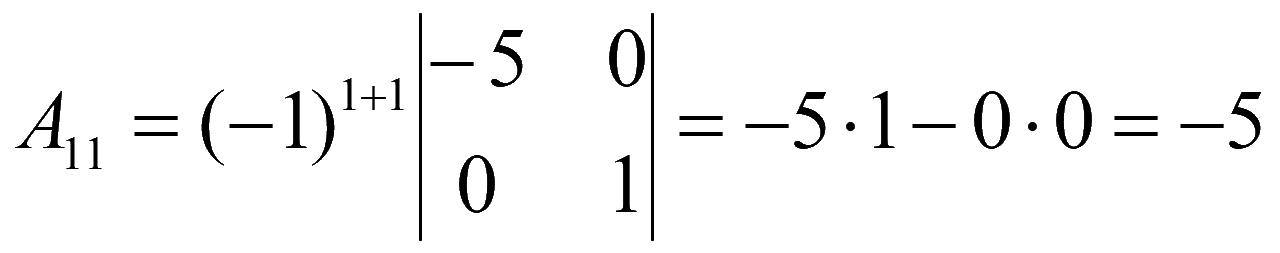
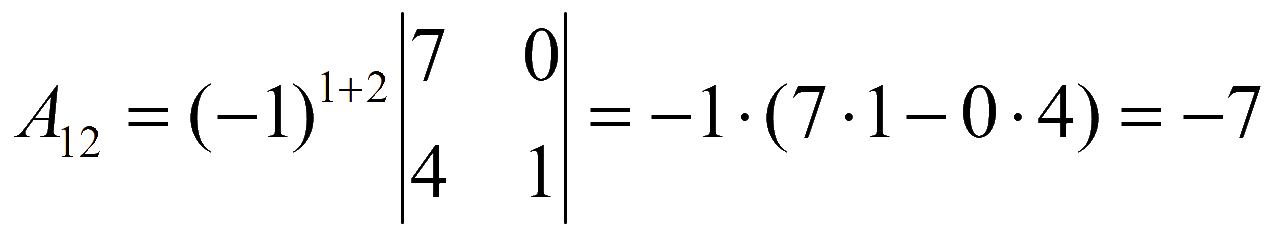
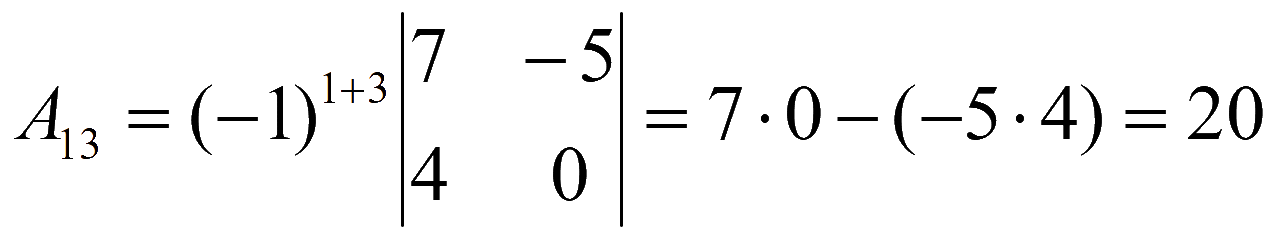
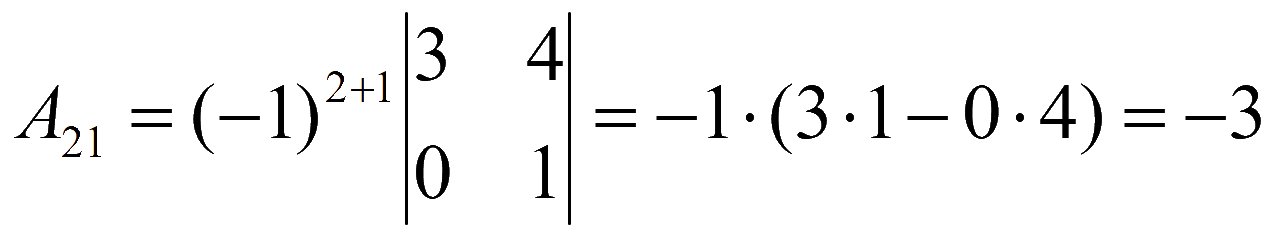
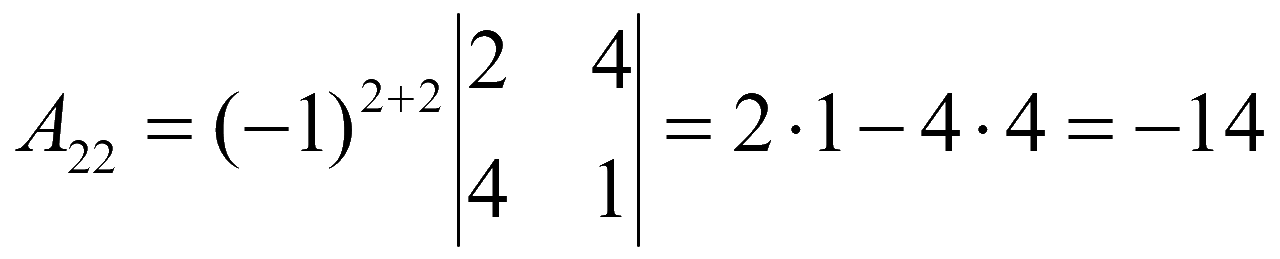
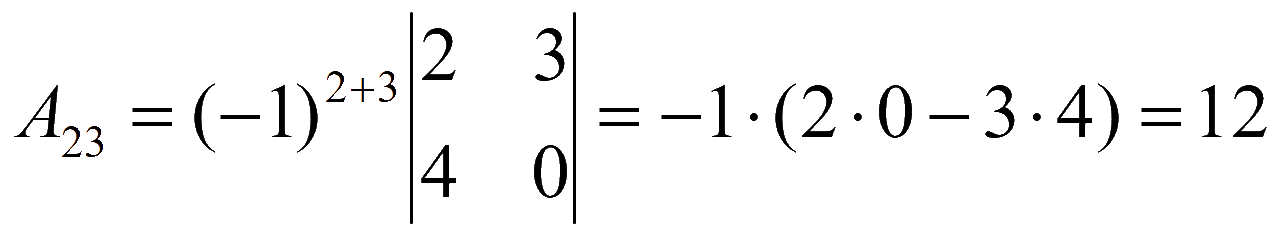
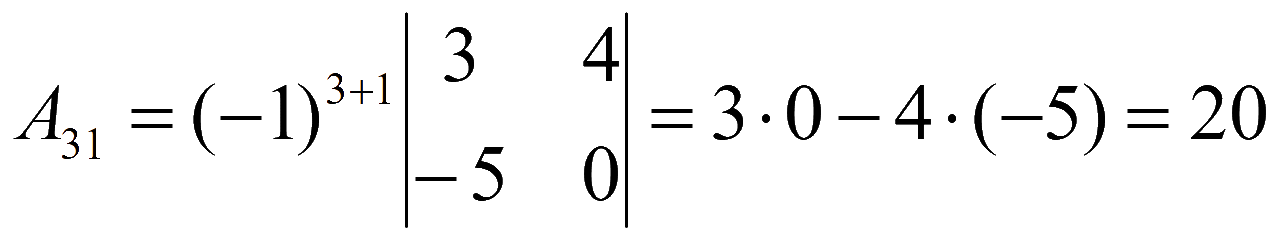
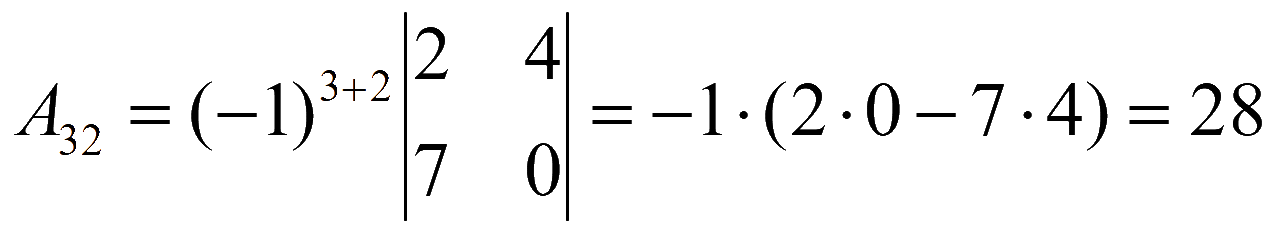
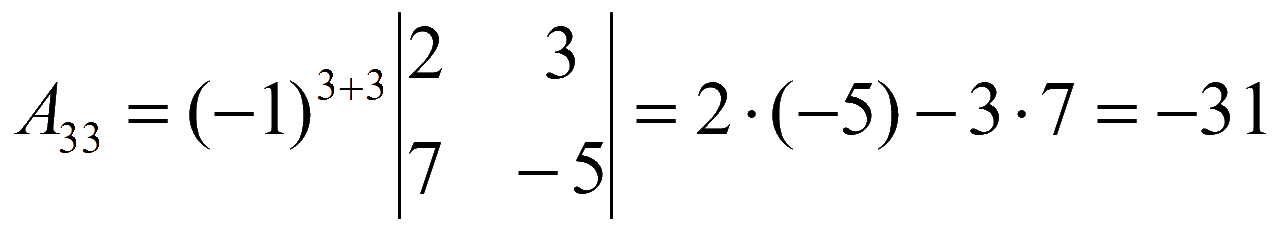
Обратная матрица

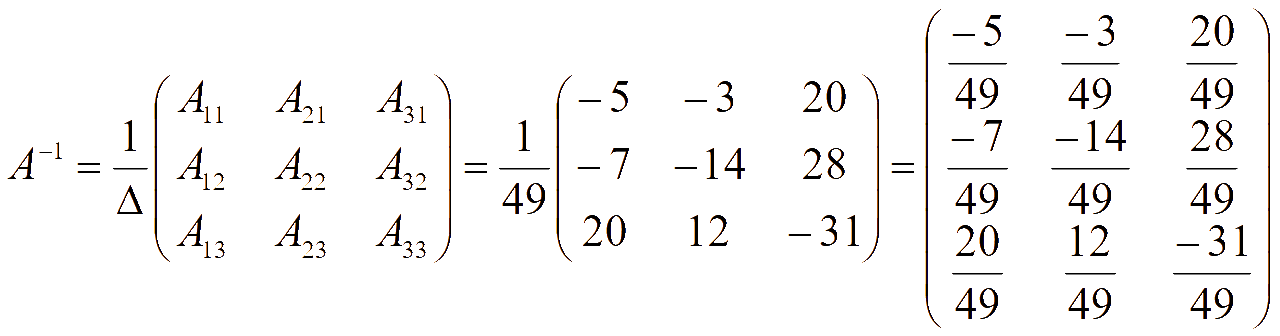
Решение системы

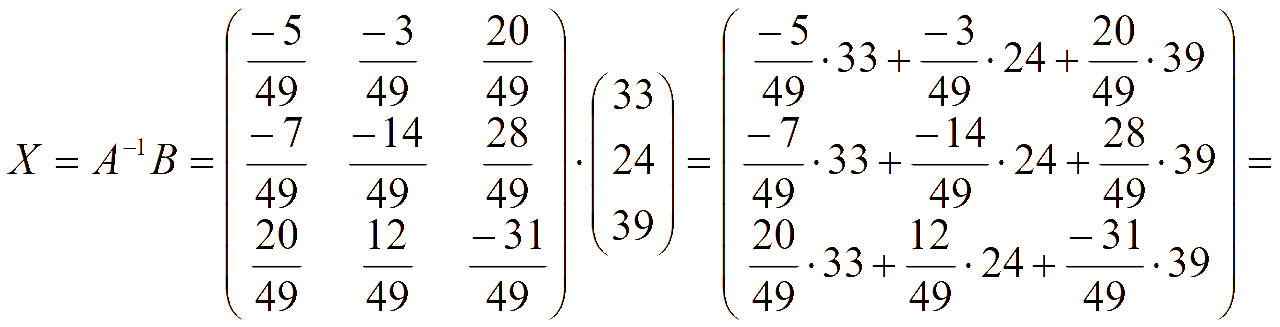
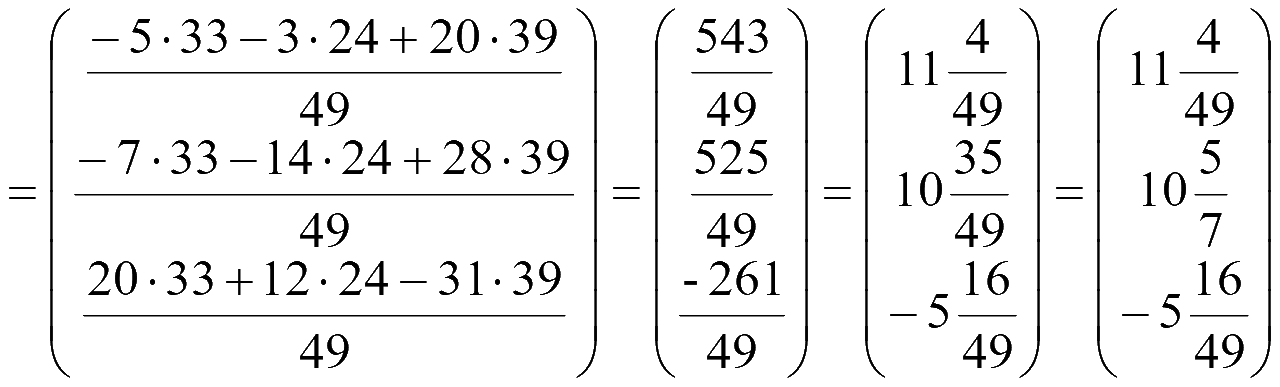
Ответ: вектор-столбец решений системы

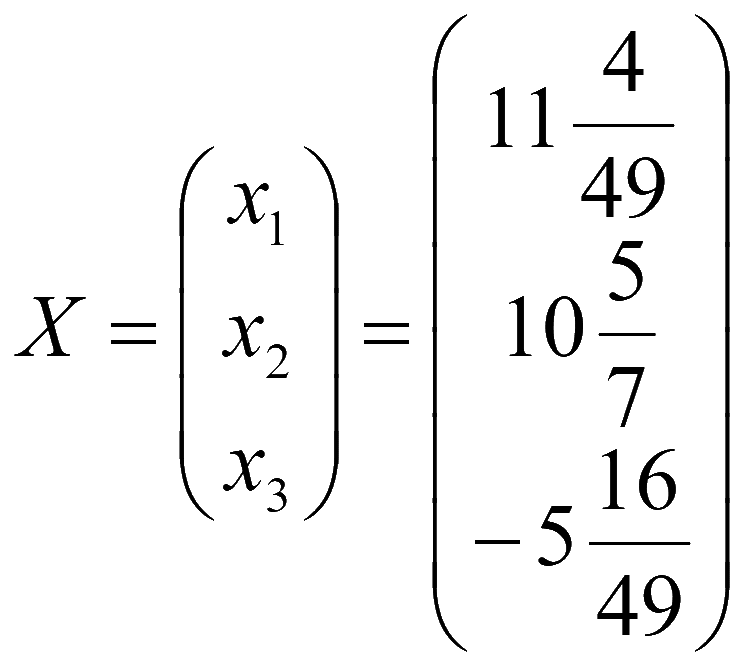
Задача. Запишите систему уравнений, соответствующую расширенной матрице и решите полученную систему уравнений

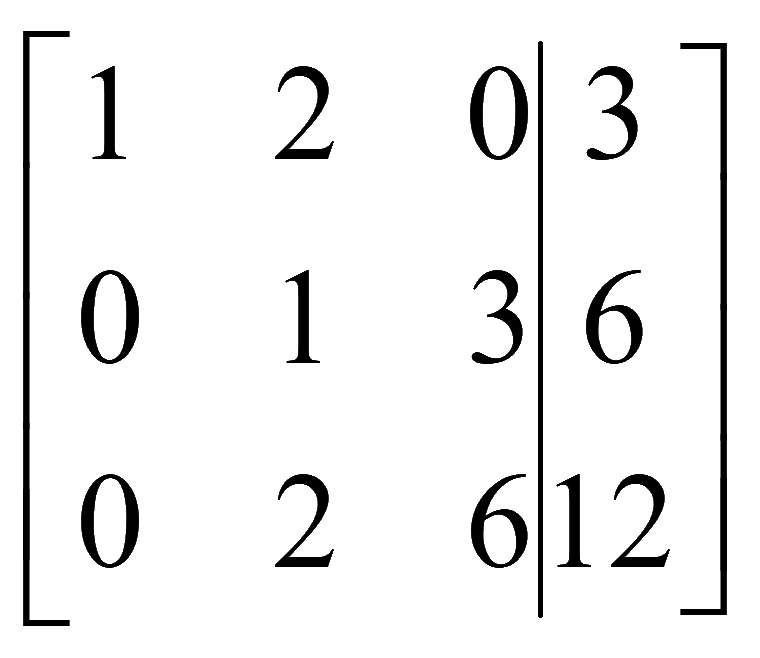
Решение

Обнулим элементы ниже главной диагонали матрицы системы. Для этого домножим 2-ю строку на (-2) и сложим 2-ю строку с 3-й строкой, результат запишем вместо 3-й строки

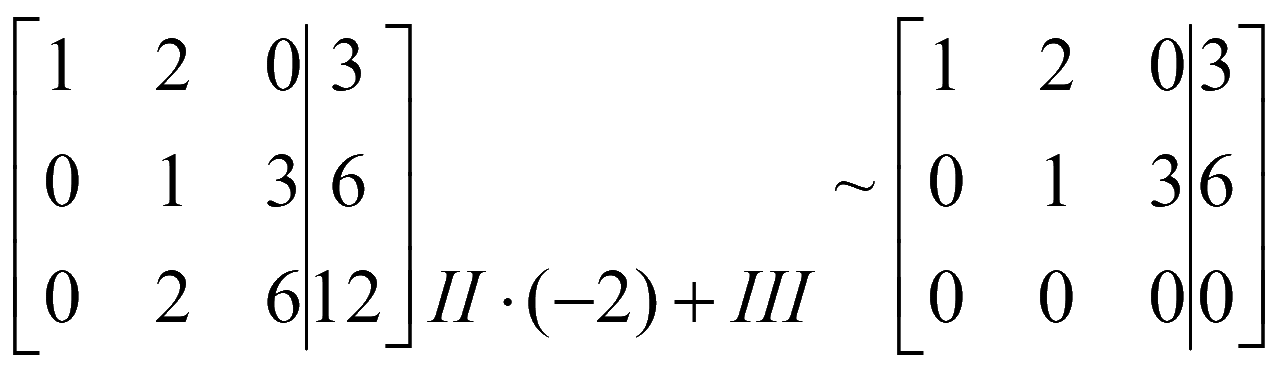
Полученной расширенной матрице соответствует система уравнений

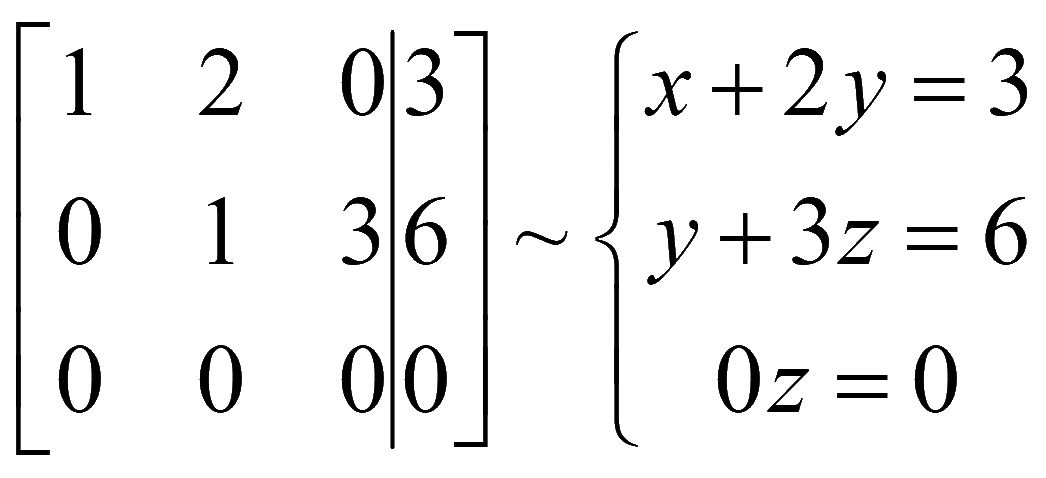
Решаем снизу вверх

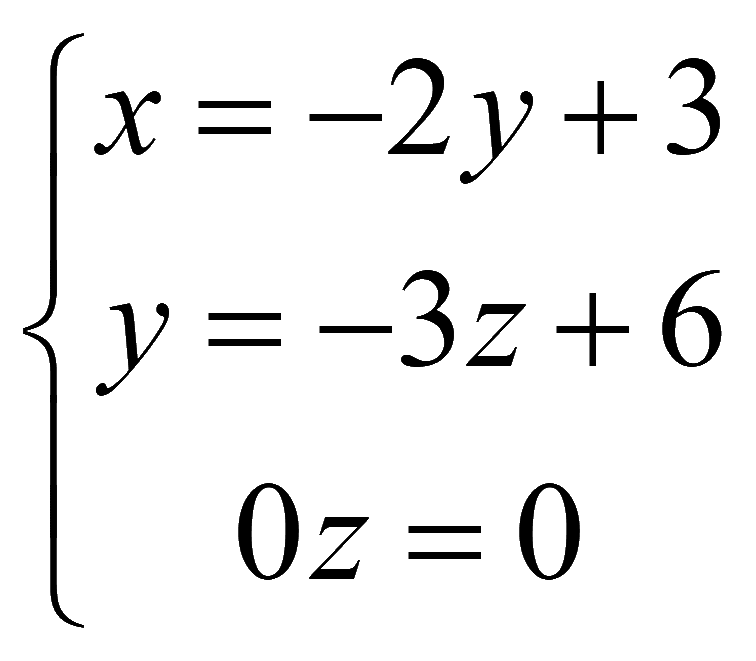
В полученной системе уравнений переменная z однозначно не определена, поэтому нельзя однозначно определить искомые переменные. Переменная z может быть любая, поэтому системе уравнений будет соответствовать бесконечное число решений.

Задача. Решить систему уравнений

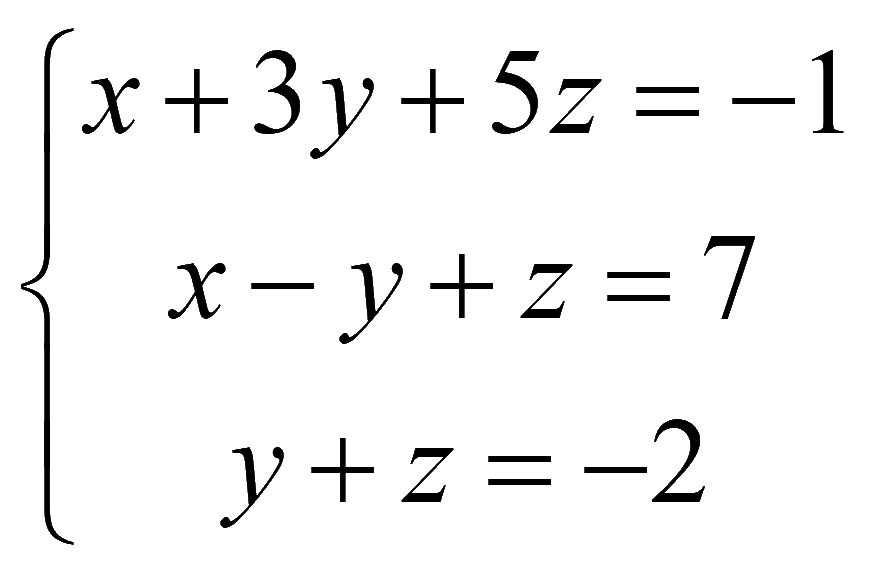
Решение

Расширенная матрица системы

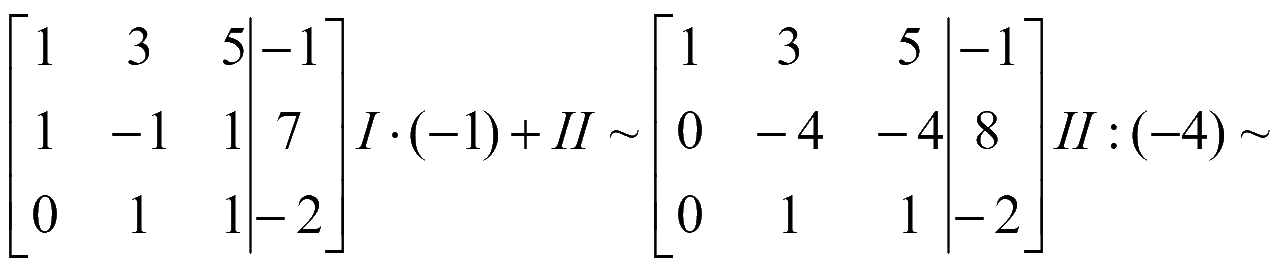
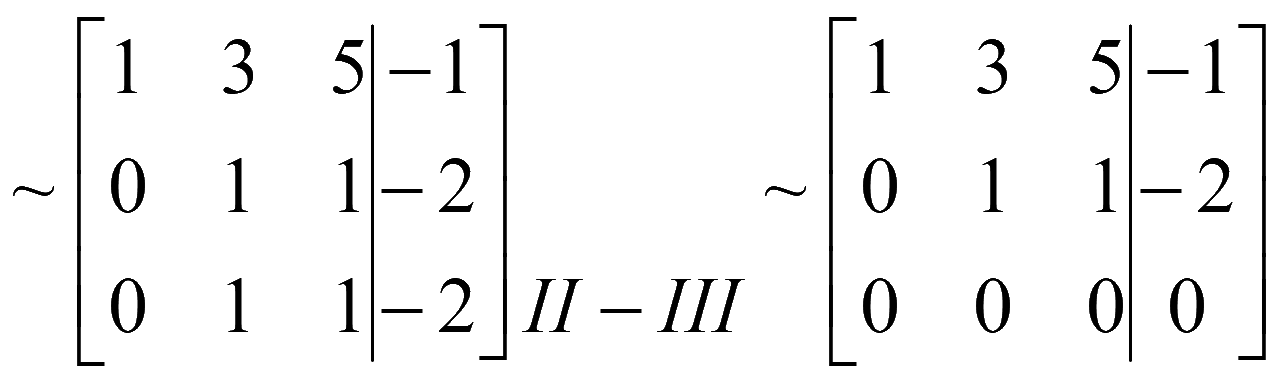
Полученной расширенной матрице соответствует система уравнений

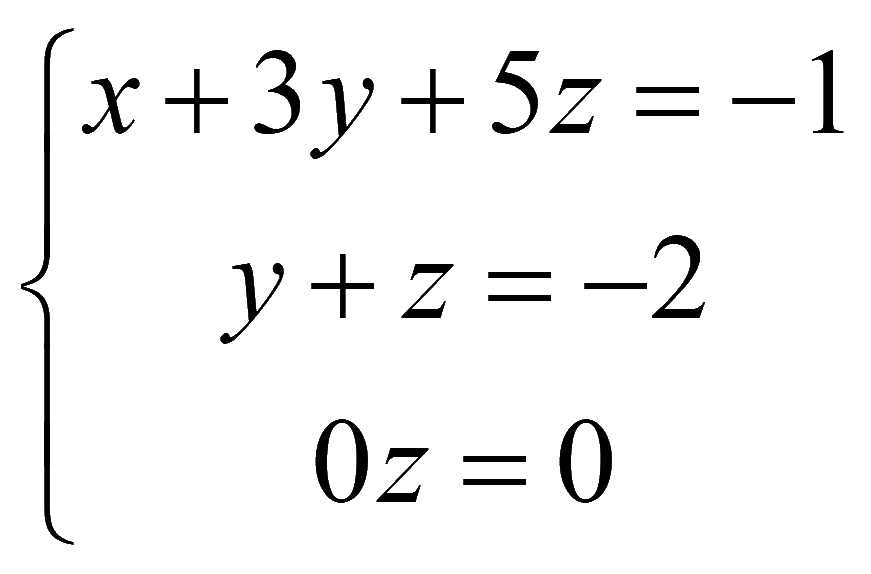
Решаем снизу вверх

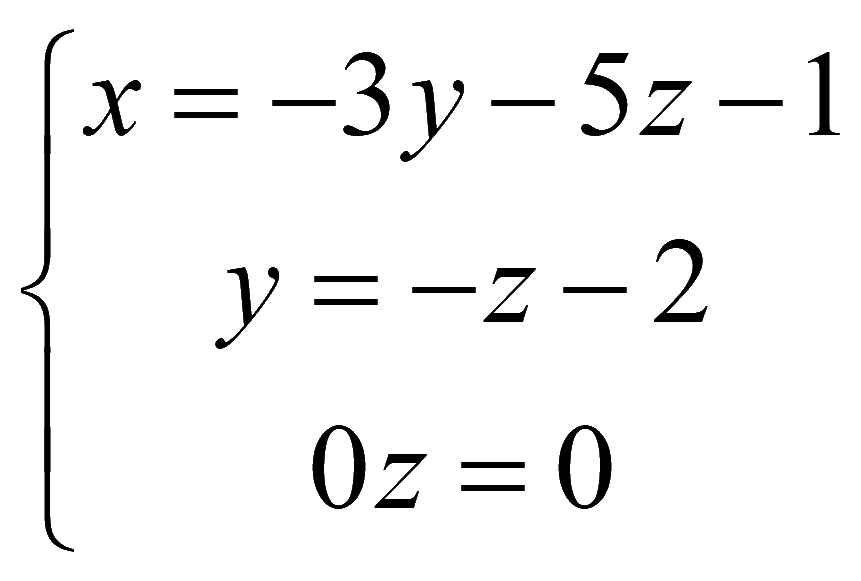
В полученной системе уравнений переменная z однозначно не определена, поэтому нельзя однозначно определить искомые переменные. Переменная z может быть любая, поэтому системе уравнений будет соответствовать бесконечное число решений.

Задача. При каких значениях m и n система уравнений имеет бесконечное число решений

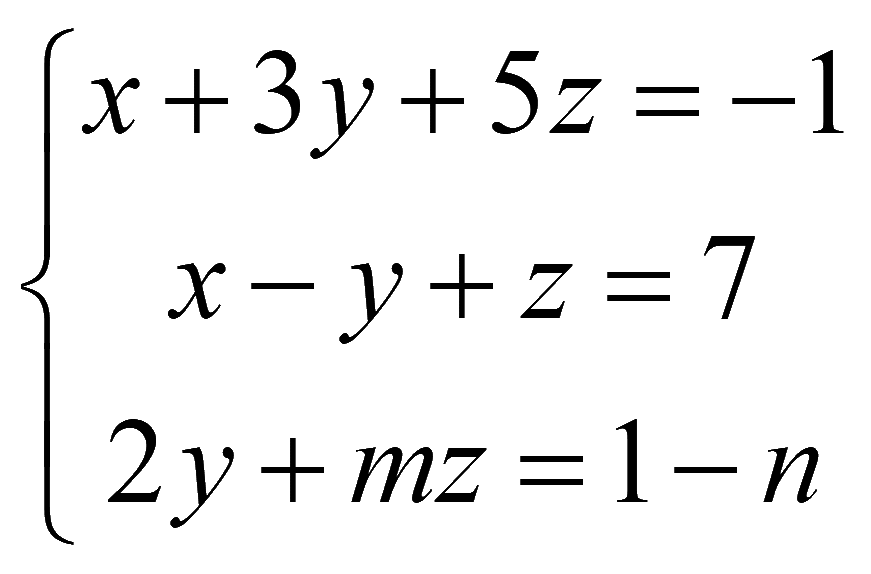
Решение

Расширенная матрица системы

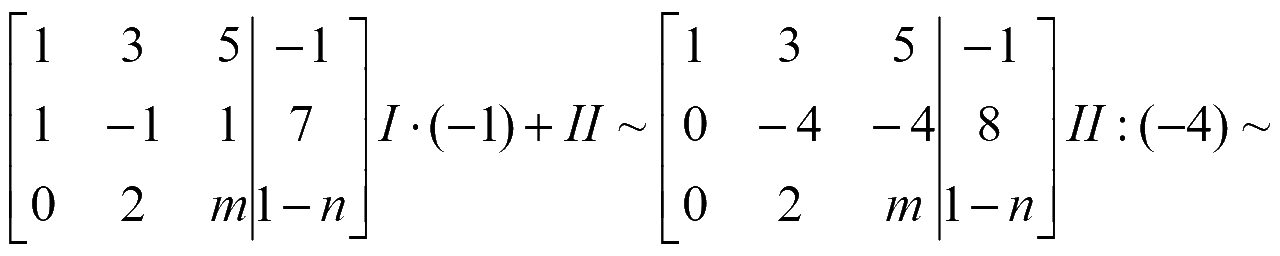
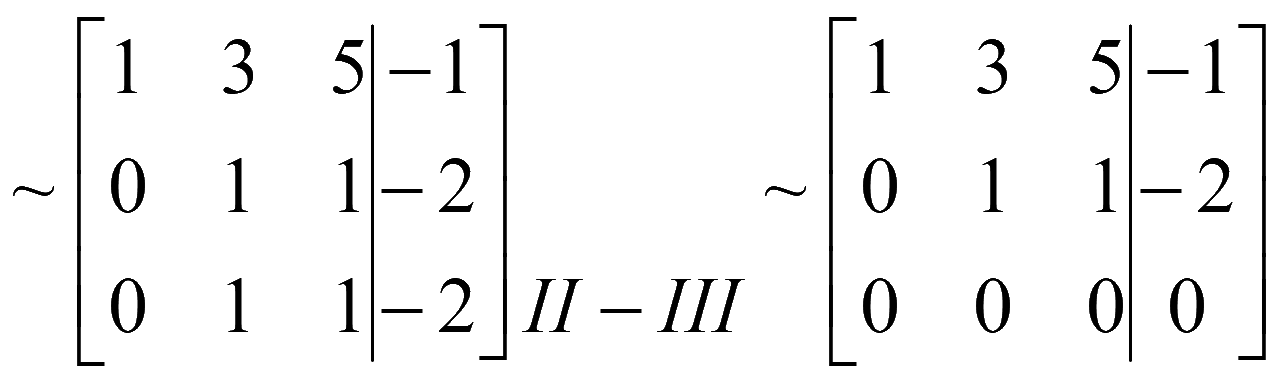
Полученной расширенной матрице соответствует система уравнений

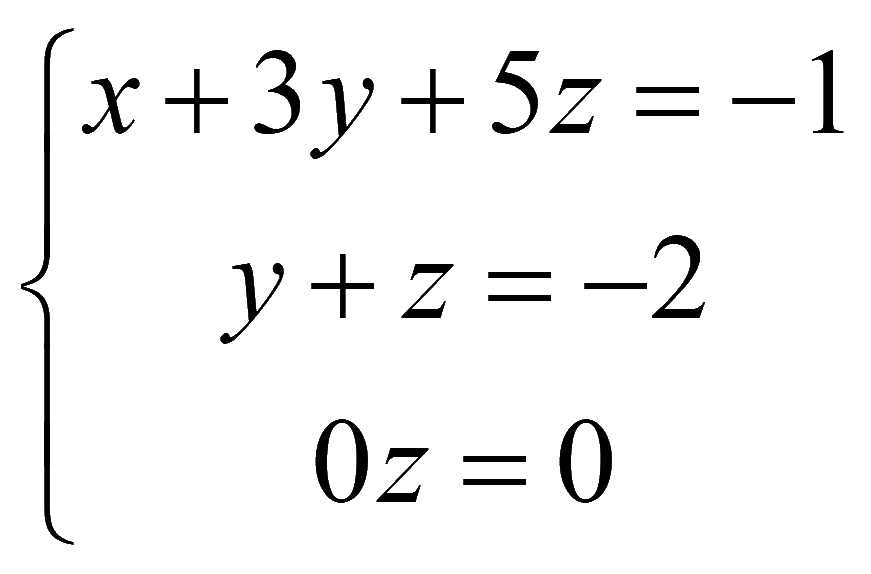
Решаем снизу вверх

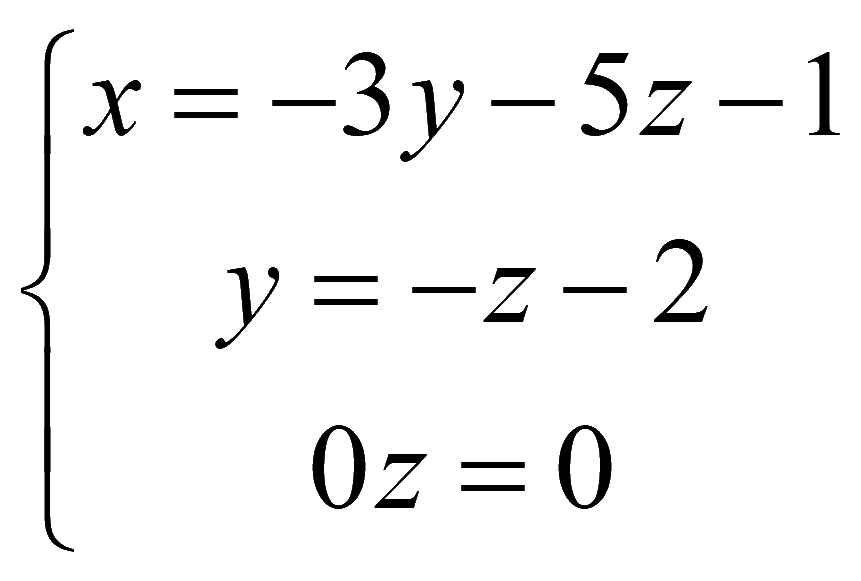
В полученной системе уравнений переменная z однозначно не определена, поэтому нельзя однозначно определить искомые переменные. Переменная z может быть любая, поэтому системе уравнений будет соответствовать бесконечное число решений.

13 Список литературы

1. Лунгу К.Н. Сборник задач по высшей математике. 1 курс / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. 7-е изд. - М.: Айрис-пресс, 2008. - 576 с.

2. Минорский В.П. Сборник задач по высшей математике. М.: Наука. - 1971 - 352с.

© 04.01.2023 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru