© 2021 Ольшевский Андрей Георгиевич репетитор по математике, информатике, физике, программированию, авиации, двигателям, электронике, искусственному интеллекту, техническим дисциплинам по Скайп da.irk.ru
Сайт super-code.ru с полезными темами, которые вы можете сохранить бесплатно
Оглавление
2 Общие принципы решения задач 4
6 Модуль 18
7 Кратное 18
Репетитор по математике, физике, информатике, техническим дисциплинам
9 Уравнения 21
12 Теорема, обратная теореме Пифагора 25
14 Степени 29
15 Одночлены и арифметические операции над ними 31
16 Многочлены и арифметические операции над ними 32
19 Формулы сокращенного умножения 36
21 Гипербола 43
22 Функции четные и нечетные 43
23 Арифметическая прогрессия 45
24 Геометрическая прогрессия 47
25 Логарифмы 49
25.1 График логарифмической функции 52
26 Обратные действия, функции 54
27 Список использованных источников 56
28 Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru 56
На современном этапе у человечества стоит задача переложить опасные, трудоемкие операции на плечи роботов, освободить себя для творческой деятельности. Математика необходима для создания математических моделей реальных задач, написания компьютерных программ с целью автоматизированного решения проблем и управления роботами.
Чем более эффективно будешь заниматься и больше времени затратишь (больше площадь круга на рисунке ниже), тем выше будет оценка.

Иногда достаточно сделать малейший шаг, чтобы увидеть в каком направлении двигаться. Если задачу не удается сразу решить, то попытаться хоть что-то сделать и это может позволить увидеть какой-то способ решения.
Из множества действий старайтесь сначала поделить, затем отнять (сократить с целью значительного упрощения, уменьшения чисел), в крайнем случае, прибавить и упорно старайтесь не умножать, так как сложение и умножение значительно увеличивают числа и являются источником потенциальных ошибок.
Лучше несколькими способами решить задачу, чем не решить или решить не правильно.
Если по 5 секунд экономить каждую минуту, то за 4 часа наберется 20 минут.
Хочешь быстро, но быстрота может привести к ошибкам и неверному результату. Перепроверка с исправлением ошибок требует меньше времени и значительно увеличивает вероятность верного результата.
Начинайте решение с нахождения области определения (области допустимых значений (ОДЗ)), так как на этой стадии может оказаться, что нет решений.
За деревьями видеть лес. То есть во множестве переменных надо увидеть формулу, заменяющую переменные на какую-то величину, которая описывается этой формулой.
Если сразу не удается вывести конечную формулу, то стоит записать все известные формулы, связанные с величинами в задаче. Имея перед собой множество формул, легче выбрать полезные и вывести конечную формулу.
Задачу можно решать с начала, развивая условие, или с конца, сразу определяя искомое. На стыке получится решение.
Неизвестную величину обычно сразу обозначают через x. Словесную формулировку задачи надо выразить уравнениями. Неявно заданную общую величину (работа, путь, время) иногда удобно принять за единицу.
Сравнивать лучше подобные, приведенные к одинаковому виду величины.
Полученное решение проверить:
на соответствие условию задачи;
оценив с другой точки зрения;
произведя грубое оценивающее решение.
Текстовые задачи являются описанием реальных задач. При решении текстовых задач создается математическая модель, то есть текст переводится в математические уравнения или систему уравнений, решение которых дает ответ. Математическая модель может быть запрограммирована и компьютерная программа будет способна найти решение при любых данных. Это позволяет выработать навык автоматизации решения любых жизненных проблем.
Производительность
![]() ,
,
отсюда работа
A = Pt.
Время
![]() .
.
Задача. Паром вышел в 12.30 из пункта A в пункт B. В пункте B он простоял 160 минут и вернулся в пункт A в 20.30. Найдите скорость парома, если расстояние между пунктами A и B 30 км, река течет из A в B со скоростью 3 км/ч.
Решение
Время стоянки в пункте B
![]()
Время отсутствия парома в пункте A
20,5 – 12,5 = 8 часов.
Время в пути
![]()
Формулы равномерного движения
![]()
![]()
s = vt.
Время движения из пункта A в пункт B по течению реки
![]()
Время движения в обратном направлении против течения реки
![]()
Общее время движения равно времени туда tAB и обратно tBA
t = tAB + tBA.
Подставляем
![]()
![]()
![]()
![]()
![]()
Сократим на 2
![]()
![]()
![]()
Получаем квадратное уравнение
8V2парома — 90Vпарома — 72 = 0;
aV2парома — bVпарома — c = 0;
D = b2 – 4ac;
![]()
![]()
![]()
![]()
Ответ: Vпарома = 12 км/ч.
Задача. Из пункта A в пункт B одновременно выехали автомобиль и велосипедист. Скорость автомобиля на 80 км/ч больше скорости велосипеда. Расстояние между пунктами A и B 30 км. Велосипедист приехал в пункт B на 2 часа 40 минут позже автомобиля. Какая скорость велосипеда?
Дано: AB = 30 км, υА = υВ + 80,
![]() .
.
Найти υВ = ?
Решение
Время движения велосипеда из A в B
![]()
Время движения автомобиля из A в B
![]()
Подставим в уравнение
![]()
![]()
![]()
Пусть υВ = x
![]()
![]()
![]()
Сократим числители на 2
![]()
![]()
![]()
Дробь равна нулю, если числитель равен нулю, но знаменатель не равен нулю (на ноль делить нельзя, поэтому 3x(x + 80) ≠ 0)
![]()
Вынесем 15 за скобки и раскроем скобки
![]()
Раскроем скобки
![]()
3x взаимоуничтожается
![]()
Сократим на 4
![]()
Домножим на -1 и переставим члены
![]()
D = b2 – 4ac;
![]()
![]()
![]()
![]()
x = -40 + 50 = 10 км/ч.
Ответ: x = 10 км/ч.
Задача.
Пароход по течению проплывает расстояние из пункта A в пункт B за 5 часов, а против течения проплывает это же расстояние от пункта B в пункт A за 7 часов. Найти время, за которое плот преодолеет расстояние от пункта A до пункта B.
Решение
Время перемещения плота по течению реки из пункта A в пункт B
![]()
Отсюда расстояние от пункта A до пункта B
![]()
Путь парохода по течению равен пути парохода против течения
![]()
Раскрываем скобки и переносим из правой части равенства в левую
![]()
Приводим подобные
![]()
Делим на 2 и выражаем скорость парохода через скорость течения
![]()
Скорость парохода получилась в 6 раз больше скорости течения.
Из двух уравнений, позволяющих выразить время движения парохода по течению и против течения, составляем систему уравнений
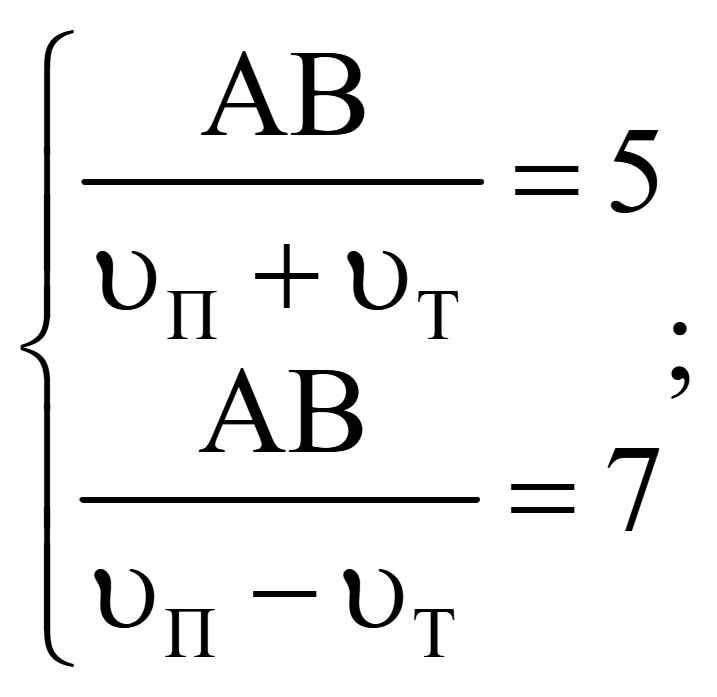
Подставляем вместо AB ранее найденный путь плота
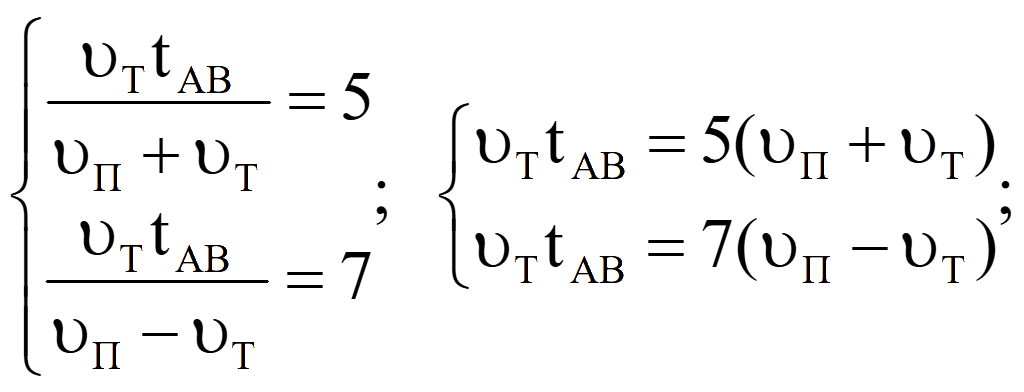
Подстановкой исключим скорость парохода
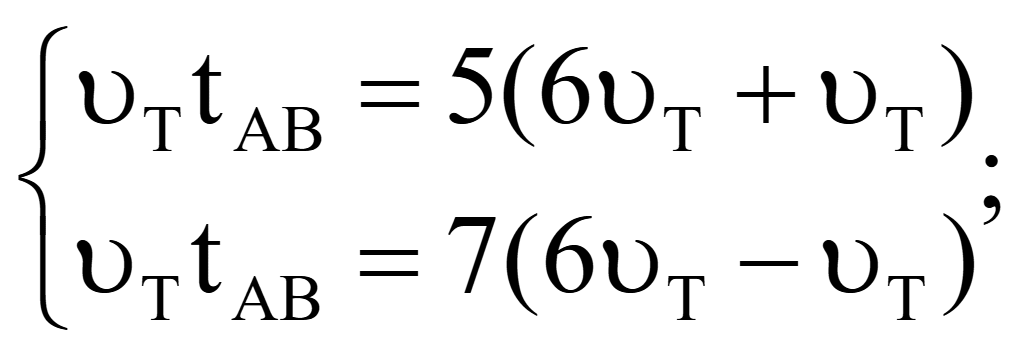
Привели подобные и раскрыли скобки
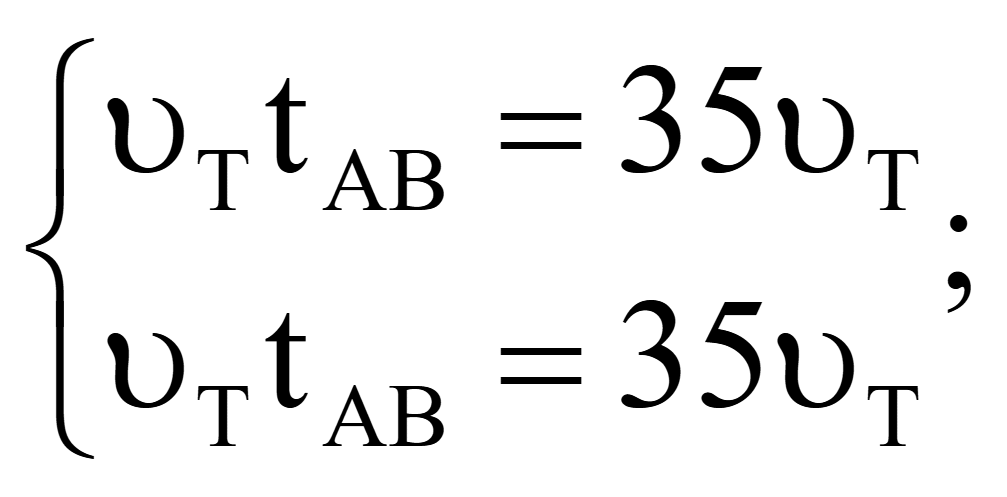
Сократили скорость течения
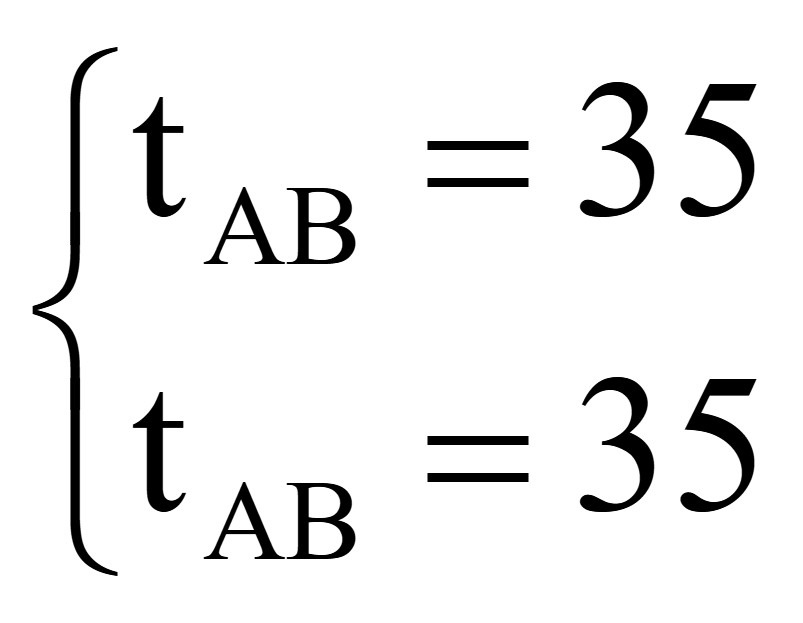
Ответ: tAB = 35 часов - время, за которое плот преодолеет расстояние от пункта A до пункта B.
Задача. Из пункта A в пункт B, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 90 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 36 минут позже автомобилиста. Ответ дайте в км/ч.
Дано:
![]()
Решение
Время езды автомобиля из A в B
![]()
Время езды велосипеда из A в B
![]()
Разница во времени
![]() .
.
Скорость автомобиля больше, подставим ее
![]()
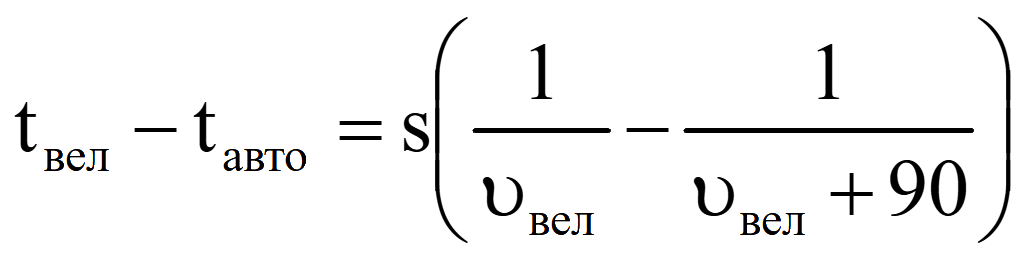
![]()
Приводим к общему знаменателю
![]()
![]()
![]()
![]() .
.
Подставим путь и разницу времени движения
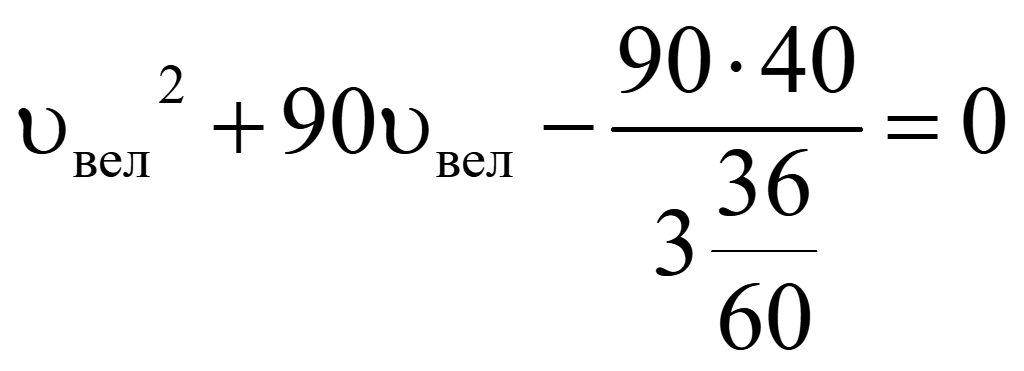
Сократим дробь в знаменателе на 12
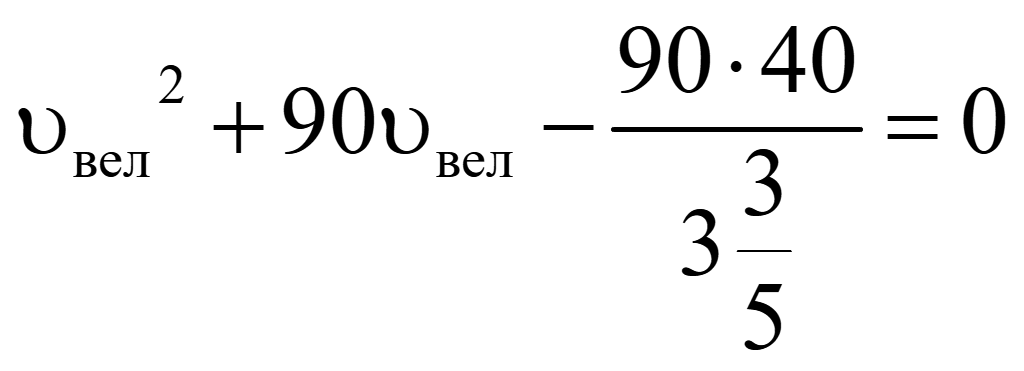
Преобразуем дробь в знаменателе в неправильную дробь
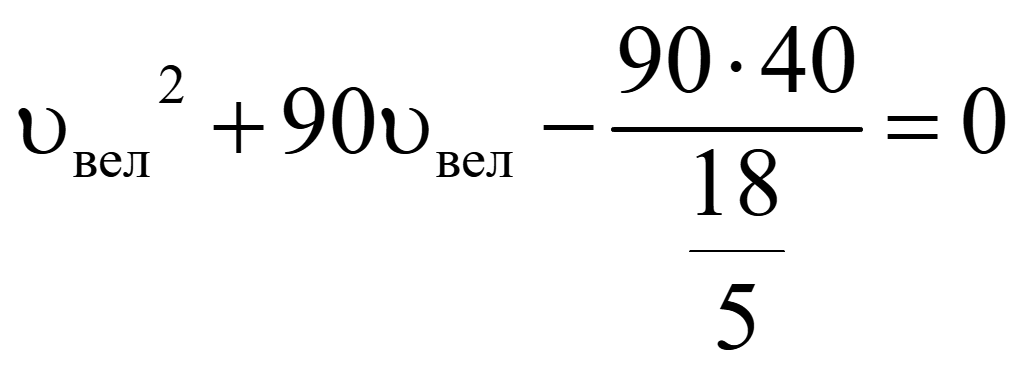
Заменим деление на дробь умножением на обратную или перевернутую дробь
![]()
![]()
![]()
![]()
По теореме Виета сумма корней равна -b = -90, а произведение корней равно c = -1000:
![]()
![]()
Система решается при двух корнях vвел1 = 10 км/ч, vвел2 = -100 км/ч. Квадратное уравнение может иметь максимально лишь 2 корня, поэтому других корней быть не может. Отрицательной скорости не бывает, поэтому скорость велосипеда
vвел = 10 км/ч.
Ответ: vвел = 10 км/ч.
Задача. Катер плыл сначала 8 часов по течению, а затем еще 10 часов против течения реки. Всего катер проплыл 264 км. Найдите собственную скорость катера, если скорость течения реки равна 3 км в час.
Дано:
![]()
Решение
Путь по течению плюс путь против течения равен общему расстоянию, которое проплыл катер
sпо + sпр = s;
Путь катера по течению равен скорости катера по течению, умноженной на время по течению
sпо = vпоtпо.
Скорость катера по течению равна скорости катера плюс скорость течения
vпо = vк + vт.
После подстановки получаем путь катера по течению
sпо = (vк + vт)tпо.
Путь катера против течения равен скорости катера против течения, умноженной на время против течения
sпр = vпрtпр.
Скорость катера против течения равна скорости катера минус скорость течения
vпо = vк - vт.
После подстановки получаем путь катера против течения
sпр = (vк – vт)tпр.
Суммируем пути по и против течения
(vк + vт)tпо + (vк – vт)tпр = s;
Подставим заданные значения
![]()
Сократим на 2 обе части уравнения
![]()
Раскроем скобки
![]()
Приводим подобные
![]()
Переносим числа в правую часть равенства
![]()
Выражаем скорость катера
![]() .
.
Ответ: 15 км/ч.
При переносе слагаемого (члена) в другую часть равенства у него меняется знак. Если необходимо поменять знак слагаемого (члена), его надо перенести в другую часть равенства.
a(b + c) = ab + ac.
a(b - c) = ab – ac.
-(b + c) = - b – c.
(b – c) = - (c - b).
При сложении чисел с разными знаками необходимо отнять от большего по модулю числа меньшее по модулю число и принять знак большего по модулю числа. Например,
1 + (-12) = -11.
Очень важно определить, что принять за 100%.
Если x ≥ 0, то |x| = x.
Если x < 0, то |x| = -x.
Кратным натурального числа а называют натуральное число, для которого а является делителем.
Обыкновенная дробь:
![]() ,
,
![]() .
.
Обыкновенная дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.
![]() ,
если a = 0, но b
≠ 0.
,
если a = 0, но b
≠ 0.
Если числитель и знаменатель обыкновенной дроби домножить на одно и то же число не равное нулю, то получим равную дробь:
![]()
Числитель и знаменатель обыкновенной дроби можно разделить на одно и то же число не равное нулю, в итоге получим равную первоначальной дробь:
![]() .
.
Складывать можно обыкновенные дроби с одинаковым знаменателем. Если знаменатели у дробей разные, то приводим дроби к общему (одинаковому) знаменателю:
![]() .
.
Общий знаменатель можно получить перемножением знаменателей. Тогда каждый знаменатель домножается на множитель, приводящий его к общему знаменателю и числитель дроби домножается на такой же множитель.
При умножении обыкновенных дробей перемножаются числители и знаменатели:
![]() .
.
Делить на дробь – значит умножить на обратную или перевернутую дробь:
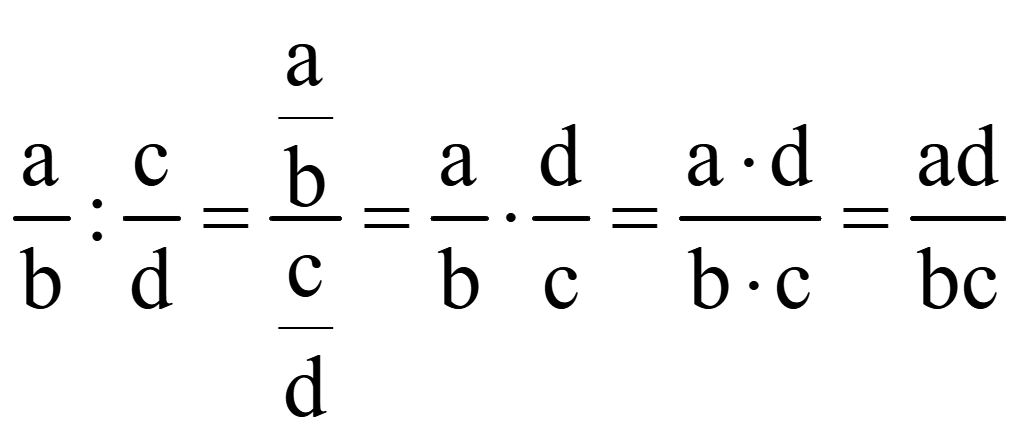 .
.
Сокращать в обыкновенной дроби можно лишь множители
![]()
![]()
![]() .
.
Слагаемые в обыкновенной дроби сокращать нельзя. Например, в дроби
![]()
нельзя сокращать a, но можно вынести слагаемое a из под общего знаменателя
![]() .
.
Число 0,012 читается «ноль целых, двенадцать тысячных»:
![]() .
.
Обыкновенные дроби можно перевести в десятичные следующим образом:
![]() ,
,
![]() .
.
При переносе слагаемого в другую часть равенства меняется знак числа или выражения:
a + b = c,
после переноса слагаемого b получаем
a = c – b.
Если в уравнении неизвестная величина x в первой степени, то члены с x переносятся в левую часть от знака равенства, а без x – в правую часть уравнения.
Чтобы из уравнения
![]()
выразить c можно обе части уравнения домножить на
![]()
![]() ,
,
слева сократится a, справа сократится c:
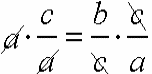
![]() .
.
Или в дроби можно менять местами c и a.
Если из уравнения a = bc необходимо выразить c, то для сокращения b, обе части уравнения надо поделить на b.
Выражение a можно записать как
![]() ,
,
то есть можно сказать, что a расположено в числителе.
При переносе выражения (или числа) из одной части равенства в другую часть от равенства, меняется расположение не являющегося слагаемым выражения:
из числителя перемещается в знаменатель
и![]()
з
знаменателя перемещается в числитель
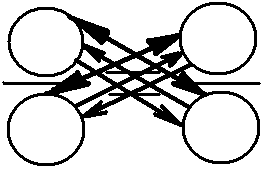
Неравенства (>, ≥, <, ≤, ≠) преобразуются также как равенства (уравнения). Разница лишь в том, что при умножении или делении обеих частей слева и справа от знака неравенства (>, ≥ или <, ≤) на отрицательное число меняются все знаки (левой части неравенства, знак самого неравенства (> меняется на <, ≥ меняется на ≤), правой части).
Неравенство (a и b числа или выражения)
ab < 0
или
![]()
выполняется если
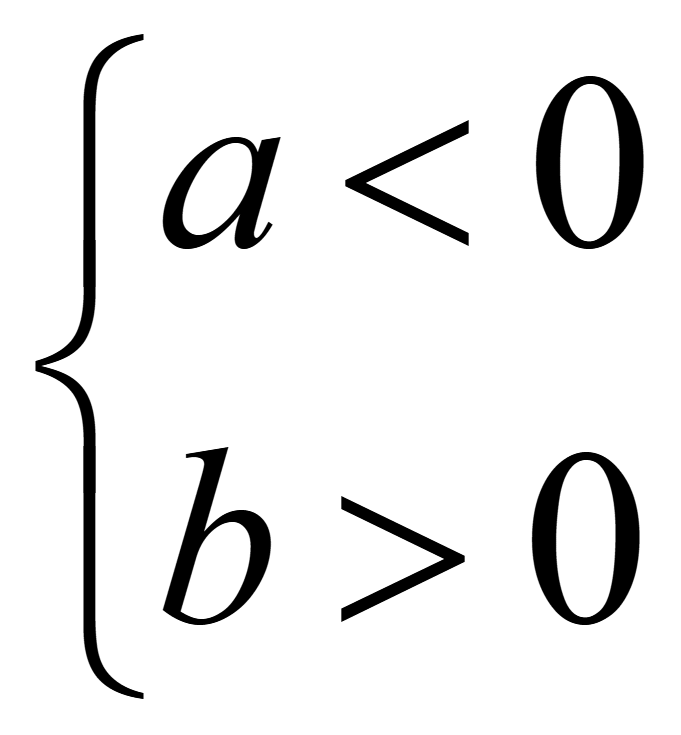 .
.
То есть минус (< 0) деленный на плюс (> 0) дает минус:
![]() .
.
Или
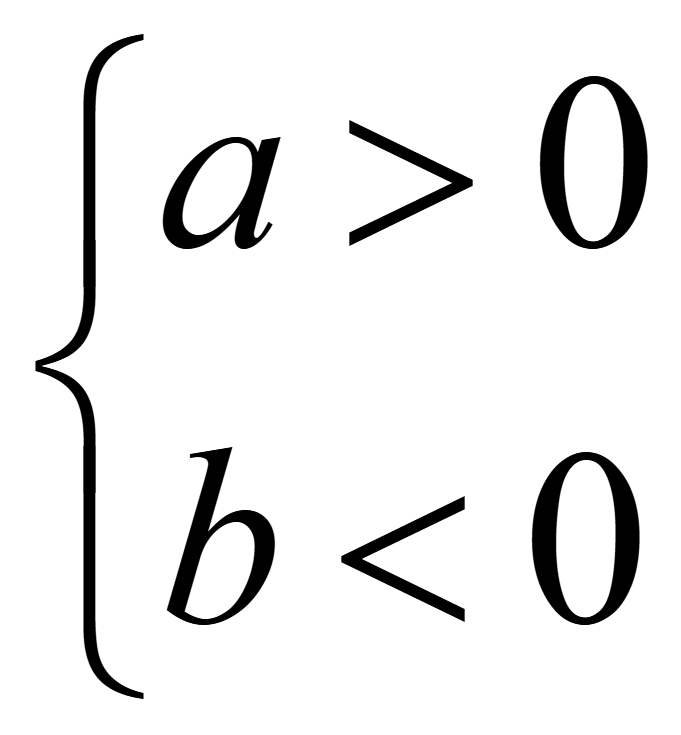 .
.
То есть плюс деленный на минус также дает минус:
![]() .
.
Неравенство
ab > 0
или
![]()
выполняется если
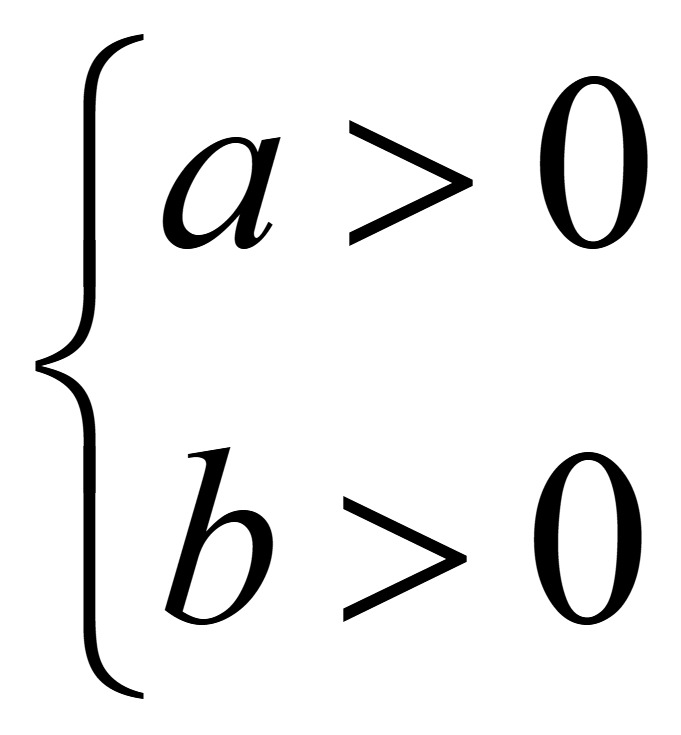 .
.
То есть плюс деленный на плюс дает плюс:
![]() .
.
Или
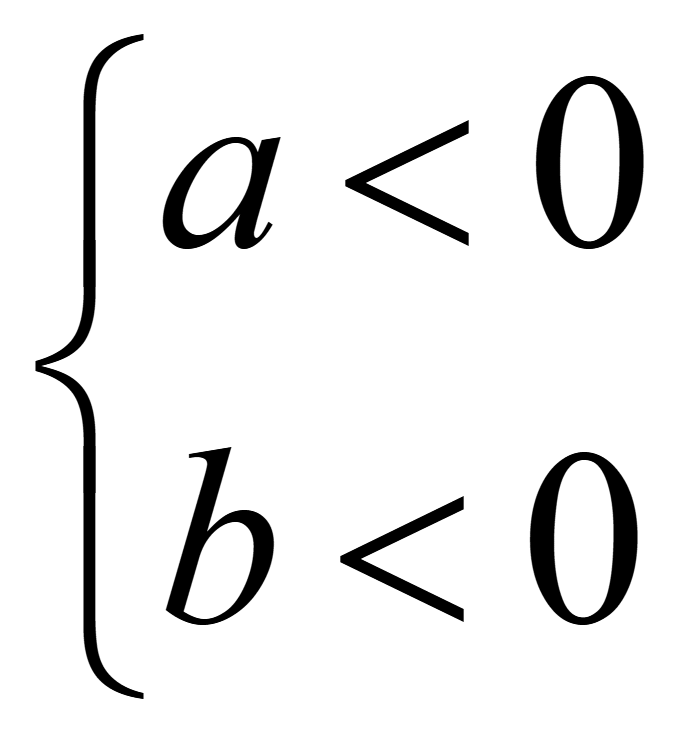 .
.
То есть минус деленный на минус также дает плюс:
![]() .
.
В неравенстве ab ≤ 0 или
![]()
знак «≤» читается: «меньше или равно». Сначала находим когда «или равно»:
![]()
при a = 0 и b ≠ 0.
Произведение ab равно нулю (ab = 0) если a = 0 или (и) b = 0.
Затем решаем неравенство «меньше» нуля ab < 0 или:
![]()
(способ решения смотрите выше).
В неравенстве
![]()
знак «≥» читается: «больше или равно». Сначала находим когда «или равно»:
![]()
если a = 0 (b ≠ 0). Затем решаем неравенство «больше» нуля:
![]()
(способ решения смотрите выше).
Квадрат гипотенузы равен сумме квадратов катетов
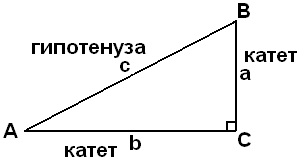
c2 = a2 + b2;
![]()
![]()
![]() .
.
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то этот треугольник прямоугольный.
Доказательство
В ∆ABC AB2 = AC2 + BC2.
Зададим ∆A1B1C1, в котором угол C1 = 900, A1C1 = AC; BC = B1C1.
A1B12 = A1C12 + B1C12.
A1B12 = AC2 + BC2.
AC2 + BC2 = AB2 = A1B12
AB = A1B1
∆ABC = ∆A1B1C1 по трем сторонам. Следовательно,
угол C = углу C1 = 900.
Следовательно, ∆ABC – прямоугольный.
Задача
В6 [1].
В треугольнике ABC AC
= BC = 4,
![]() .
.
Найти AB.
Решение

![]()
![]()
Из теоремы Пифагора
![]()
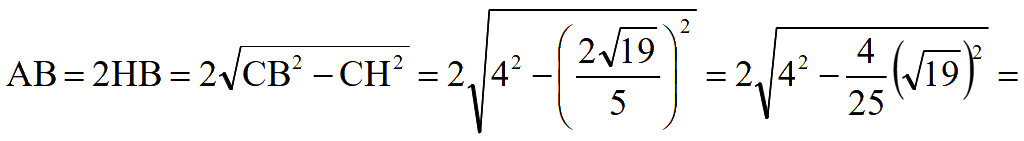
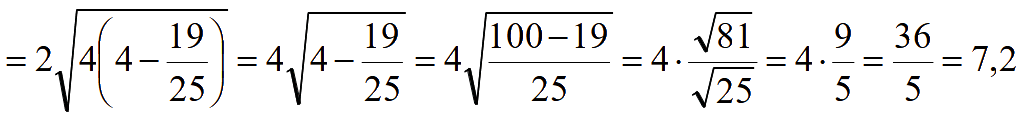
Ответ: AB = 7,2.
Графиком линейной функции является прямая.
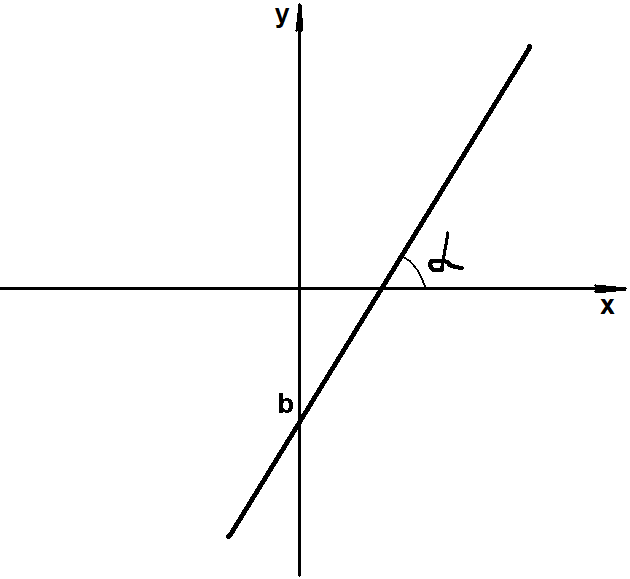
Уравнение прямой с угловым коэффициентом
y = kx + b,
где k – угловой коэффициент наклона прямой;
x – аргумент функции;
b – отрезок, отсекаемый на оси y.
α - угол наклона прямой к оси x.
![]() .
.
Если угол α острый, то
![]() .
.
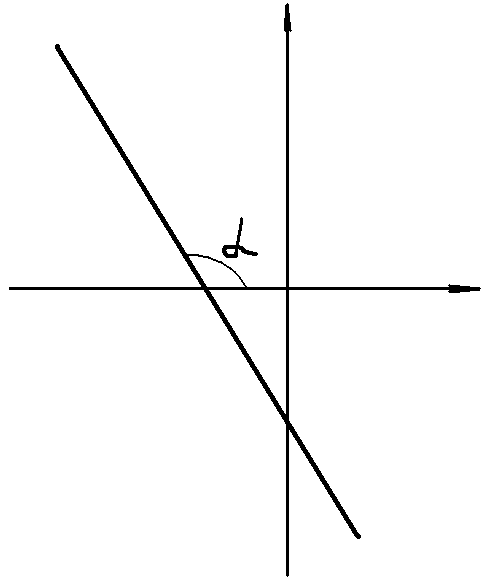
Если угол α тупой, то
![]() .
.
Задача. Найти угловой коэффициент прямой, заданной уравнением
3x + 4y – 6 = 0
Решение
Найдем уравнение прямой с угловым коэффициентом
4y = -3x + 6
![]()
![]()
y = - 0,75x + 1,5
Ответ: k = - 0,75.
Степень
an,
где a – основание степени;
n – показатель степени.
При n ≤ 0 основание не должно быть равно нулю
a ≠ 0,
так как выражения 00 и 0n лишены смысла. При n < 0 ноль в отрицательной степени преобразуется в деление на 0, а это недопустимо.
При n > 0
0n = 0.
Степень является перемножением основания a n раз:
![]() .
.
При любом выражении a выражение в квадрате больше или равно нулю:
a2 ≥ 0.
Например, (-2)2 = 4 и 22 = 4.
При любом выражении a выражение в четной степени 2n больше или равно нулю:
a2n ≥ 0.
Выражение a в нечетной степени 2n + 1
a2n + 1
может иметь любой знак.
При смене знака показателя степени, степень перемещается из числителя в знаменатель или из знаменателя в числитель:
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
в частности
![]() ;
;
![]()
Любое выражение, отличное от нуля, в степени 0 равно 1
a0 = 1.
Единица в любой степени равна единице:
1n = 1; 1 = 12; 1 = 13; 1 = 1n.
Умножение и деление степеней с одинаковым основанием или показателем степени. При умножении степеней с одинаковым основанием показатели степеней складываются
![]() ;
;
![]()
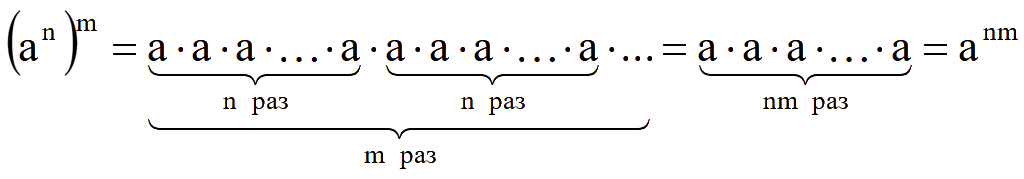
![]()
![]()
При делении степеней с одинаковым основанием показатели степеней отнимаются
![]() ;
;
![]() .
.
Способы раскрывания скобок в степенях
![]()
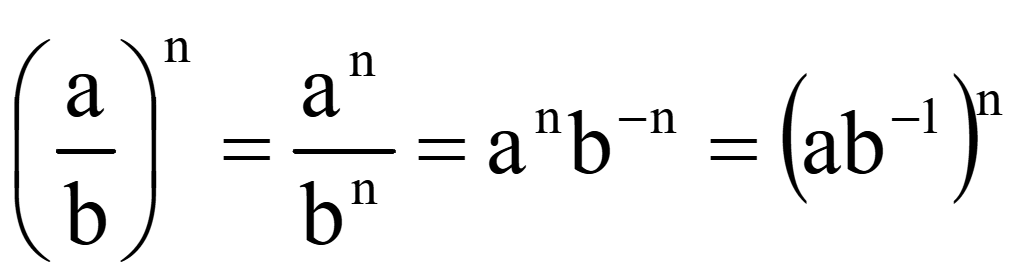
(ab)n = anbn.
Корень
n – ной степени от выражения равен
выражению в степени
![]() :
:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
Арифметический квадратный корень положительный, отрицательное число в квадрате становится положительным, поэтому необходим модуль, чтобы возможное отрицательное число a превратить в положительное с помощью модуля
![]()
В следующем случае модуль не требуется так как под корнем должно быть a ≥ 0
![]()
![]() ;
;
![]() ;
;
![]()
Вычислить
![]() .
.
Решение
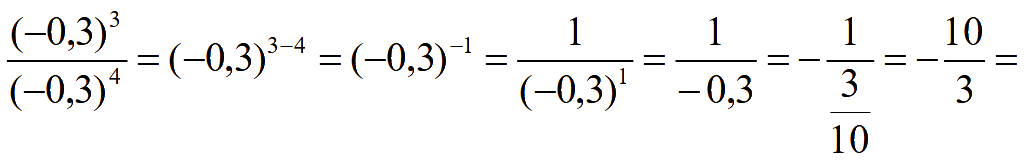
![]() .
.
Одночленами являются числа, переменные, произведение чисел, переменных и степени переменных. Член, содержащий деление на переменную не является одночленом.
Чтобы привести любой одночлен к стандартному виду надо перемножить числовые множители и полученный коэффициент одночлена записать на первом месте, затем перемножая степени с одинаковыми переменными в основании, записать их и остальные переменные в виде множителей.
Одночлены с одинаковыми переменными, возведенными в одинаковую степень, называются подобными. Подобные одночлены, предварительно приведенные к стандартному виду, можно складывать, суммируя их коэффициенты, которые могут быть положительными или отрицательными. Если одночлен не имеет коэффициента, то подразумевается, что коэффициент равен 1.
Умножение одночленов дает новый одночлен, который требуется привести к стандартному виду. Возведение одночлена в степень фактически является многократным перемножением одночленов и выполняется по правилам возведения в степень.
Многочлен — это сумма одночленов.
Умножение многочлена на одночлен происходит по распределительному закону умножения:
(a + b)c = ac + bc,
где a, b, c – одночлены.
Степенной называется функция
y = xr,
где r – рациональное число.
Задача 12.10. Постройте график функции
y = -(x +2)3 – 1
Построение
График функции y = -(x +2)3 – 1 получается из графика функции y = x3
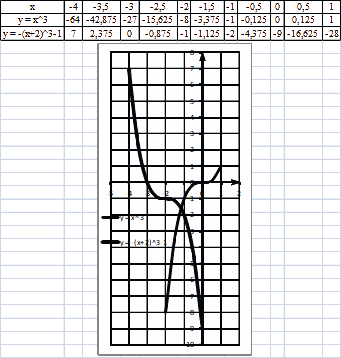
симметричным отображением относительно оси OX, смещением влево на 2 единицы и смещением вниз на 1 единицу.
Показательной называется функция
y = ax,
где a – основание, постоянная a > 0 и a ≠ 1.
При a > 1 функция y = ax возрастает. Построим график показательной функции y = 2x.
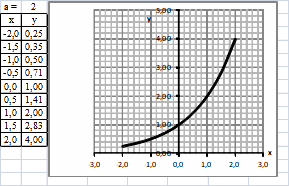
Касательная к графику функции y = 2x в точке (0; 1) составляет угол с осью Ox менее 450.
Построим график показательной функции y = 3x.
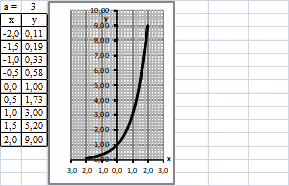
Касательная к графику функции y = 3x в точке (0; 1) составляет угол с осью Ox более 450.
Было найдено такое число e, при котором касательная к графику функции y = ex в точке (0; 1) составляет угол с осью Ox 450. Число e в диапазоне 2 < e < 3, примерно оно равно e ≈ 2,72. Показательную функцию y = ex с основанием e и ее график называют экспонентой
y = ex = exp(x).
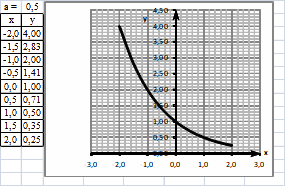
При
a < 1 функция y
= ax
убывает. Построим график показательной функции
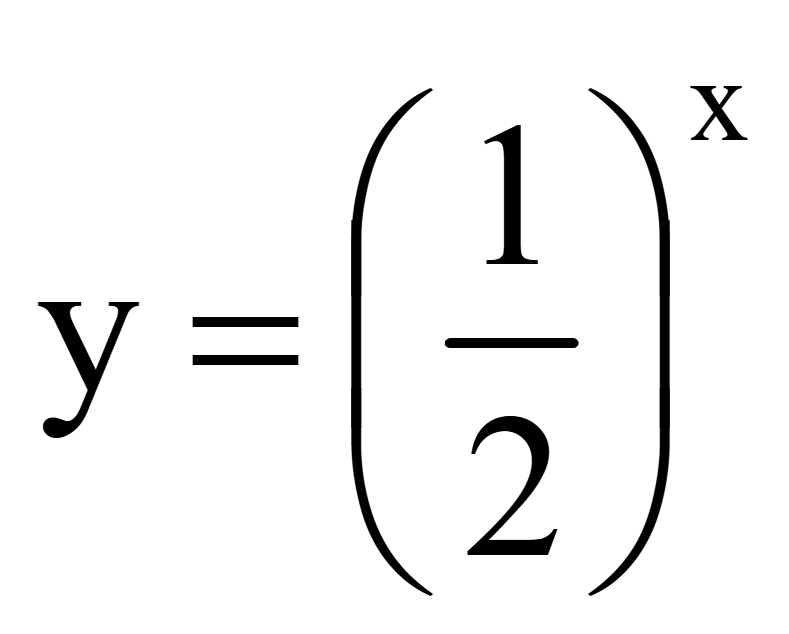 .
.
Если уравнение удается свести к виду
af(x) = ag(x),
в котором основания равны, то показатели степени также равны
f(x) = g(x).
В формулах сокращенного умножения скобки присутствуют лишь в одной части равенства.
Квадрат суммы (a + b)2 = a2 + 2ab + b2.
Квадрат разности (a - b)2 = a2 - 2ab + b2.
Разность квадратов a2 - b2 = (a - b)(a + b).
Разность кубов a3 - b3 = (a - b)(a2 + ab + b2).
Сумма кубов a3 + b3 = (a + b)(a2 – ab + b2).
Куб разности (a - b)3 = a3 - 3a2b + 3ab2 - b3.
Куб суммы (a + b)3 = a3 + 3a2b + 3ab2 + b3.
Последние две формулы являются следствием бинома Ньютона:
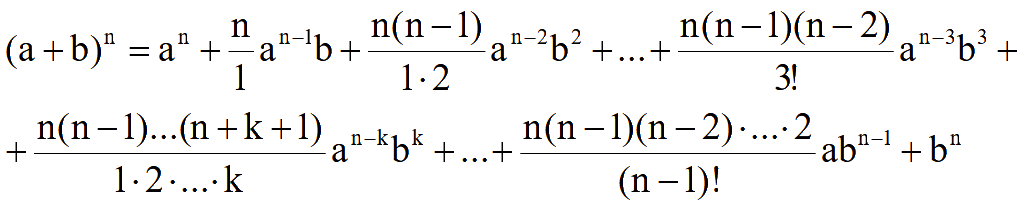
В выражении в четной степени можно поменять знаки всех слагаемых. Для квадрата разности можно записать:
(a - b)2 = a2 - 2ab + b2 = b2 - 2ab + a2 = (a - b)2.
(a - b)2 = (a - b)2.
Квадратное уравнение
ax2 + bx + c = 0.
Дискриминант
D = b2 - 4ac.
Если D > 0, то квадратное уравнение имеет два различных корня
![]()
Если D = 0, то квадратное уравнение имеет два одинаковых корня
![]()
Если D < 0, то действительных корней нет.
Графиком квадратичной функции
![]()
является парабола. Она получается из графика функции
![]()
смещением вершины параболы по осям x и y, а также сжатием или растяжением вдоль оси x.
Для определения координаты xв вершины параболы вынесем из под общего знаменателя формулу определения корней квадратного уравнения
![]()
Отсюда координата вершины параболы
![]()
Координата yв вершины параболы может быть найдена подстановкой координаты xв в уравнение параболы.
Для нахождения координат вершины параболы выделим полный квадрат
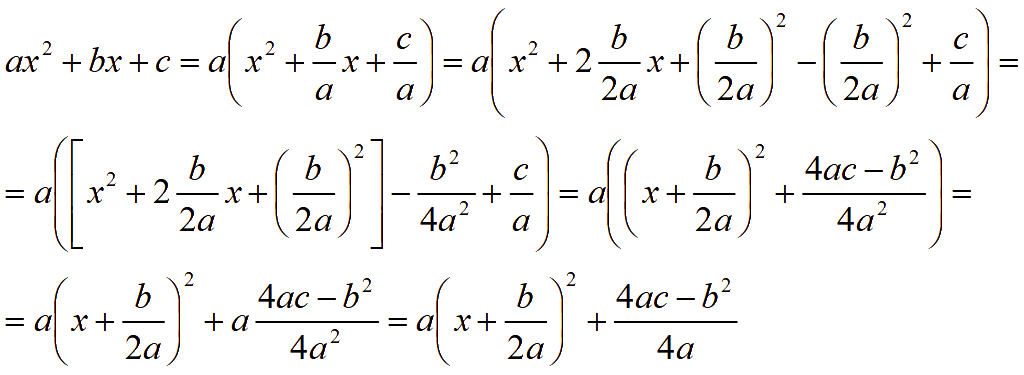
График этой функции получается из графика функции
![]()
смещением по оси x на
![]()
единиц влево и смещением по оси y на
![]()
единиц вверх.
Координата x вершины параболы
![]() .
.
Координата y вершины
![]()
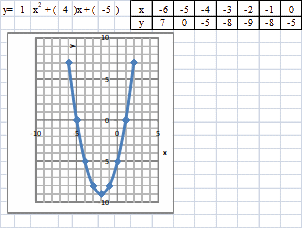
При пересечении оси x координата y равна нулю, получается квадратное уравнение
![]()
Точки пересечения оси x являются корнями квадратного уравнения, т. е. при подстановке x1 и x2 квадратное уравнение становится равным нулю.
По формулам сокращенного умножения квадрат суммы
![]() .
.
Правая часть равенства называется полным квадратом суммы.
Квадрат разности
![]() .
.
Правая часть равенства называется полным квадратом разности.
Разность квадратов
![]() .
.
Выделим полный квадрат из квадратного уравнения
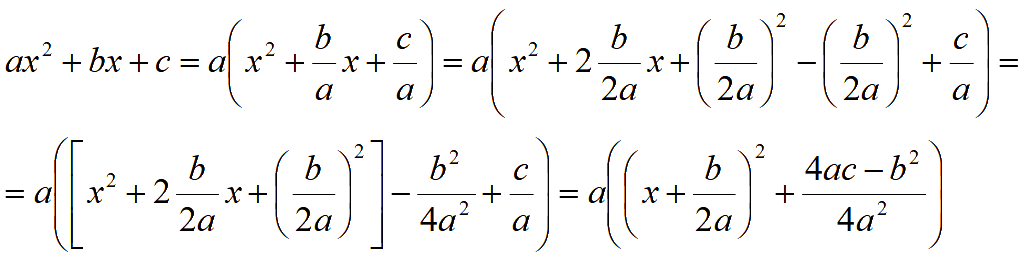
Получили функцию
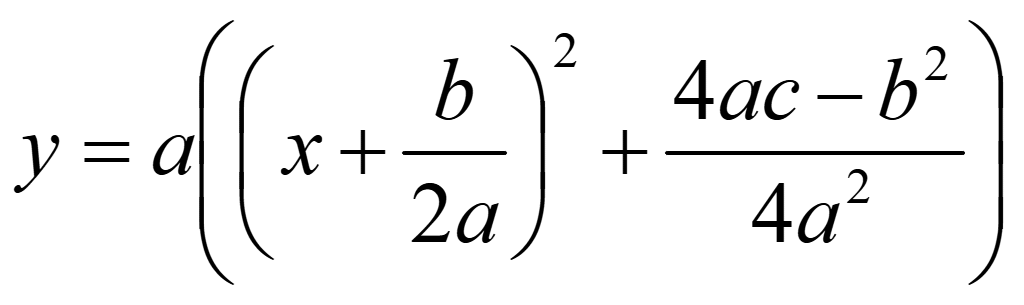 ,
,
она пересекает ось x при y = 0:
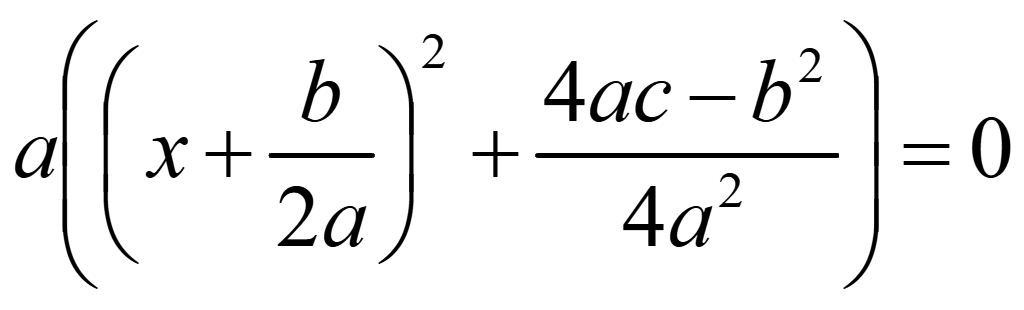 .
.
a ≠ 0, следовательно
![]() .
.
Для нахождения при каких x уравнение равно нулю разложим уравнение на множители, выделив разность квадратов. Вынесем минус из второй дроби
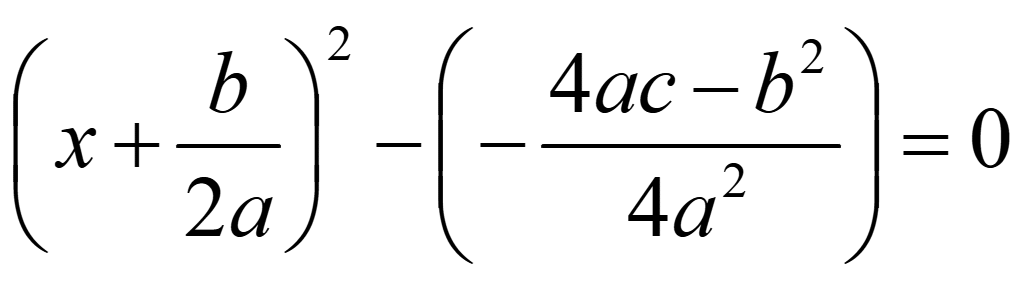
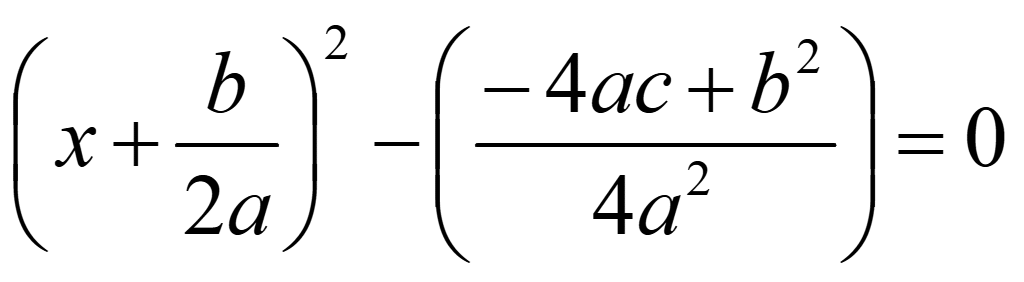
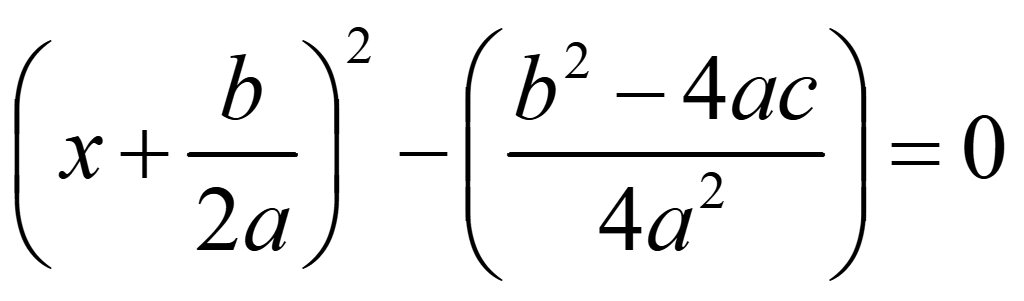
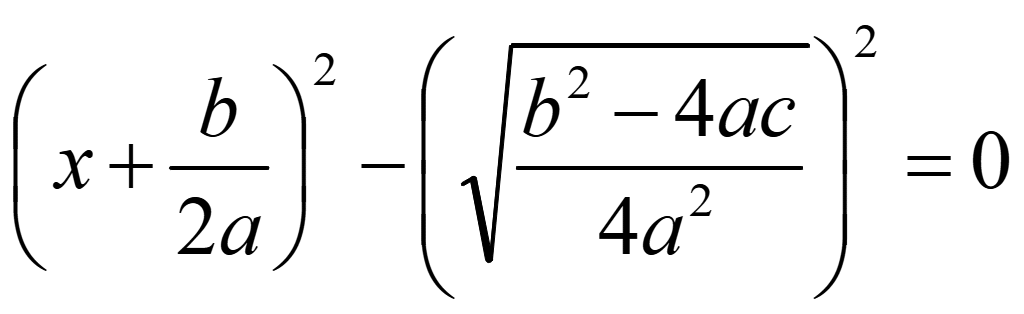
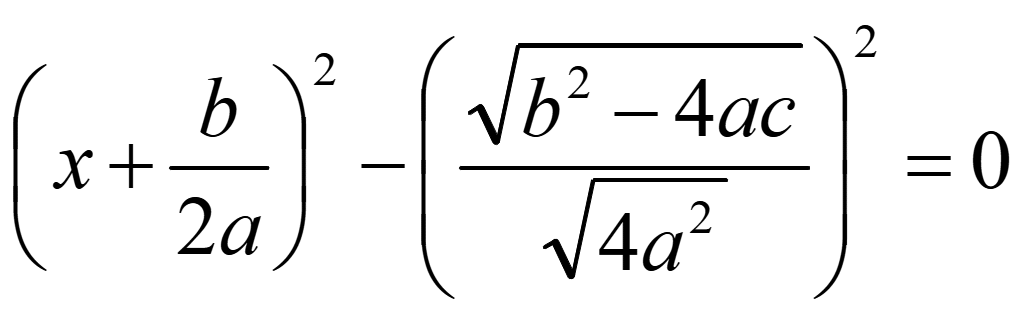
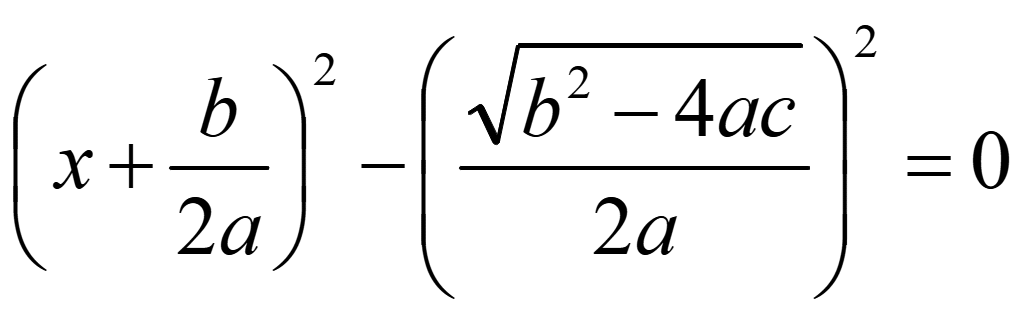
Разложим разность квадратов
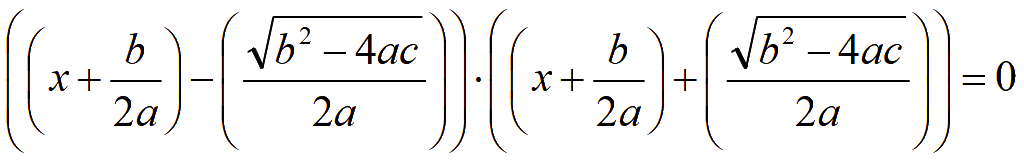
Уберем скобки
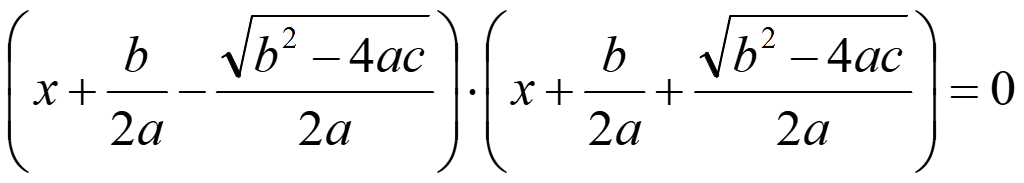
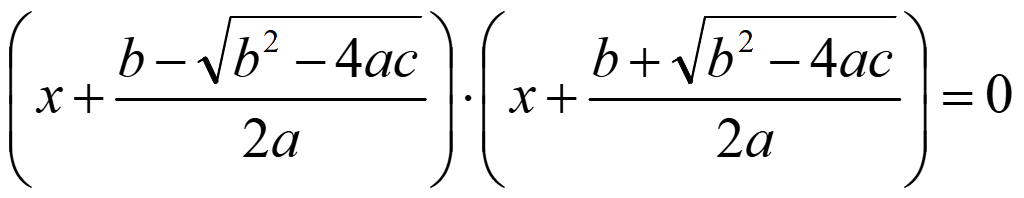
Выражение равно нулю, когда либо
![]()
или
![]()
![]()
или
![]()
В общем имеем два корня
![]()
Выражение под корнем назвали дискриминантом
![]()
и дискриминант должен быть
![]() .
.
Если
![]() ,
,
то будет два одинаковых корня
![]() .
.
При
![]()
действительных корней нет.
Корни квадратного уравнения
![]()
![]()
![]() ,
,
где xв – координата x вершины параболы
![]()
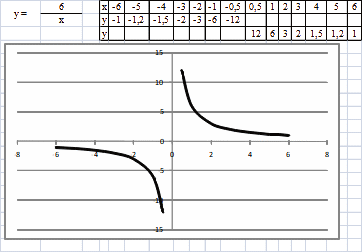
Четная функция f(-x) = f(x) симметрична относительно оси OY на всей области определения. Например, функция y = x2 на интервале [- 4; 4] четная.
Нечетная функция f(-x) = - f(x) симметрична относительно начала координат на всей области определения. Например, функция y = x3 на интервале [- 4; 4] нечетная.
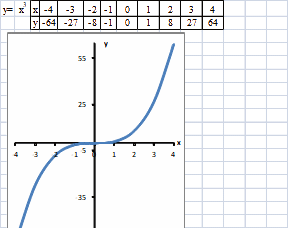
Функция общего вида ни четная и ни нечетная, она не симметрична относительно оси OY и начала координат. Если область определения функции не симметрична, то функция ни четная, ни нечетная. Например, функции y = x2 на интервале [-4; 4) и y = x3 на интервале (- 4; 4] ни четные и ни нечетные.
Задача. Исследовать на четность функцию y = 2x + 1.
Решение
f(-x) = -2x + 1 ≠ f(x) = 2x + 1,
следовательно, функция не является четной.
f(-x) = -2x + 1 ≠ -f(x) = -2x - 1,
следовательно, функция не является нечетной.
f(-x) ≠ f(x) и f(-x) ≠ -f(x), заданная функция ни четная, ни нечетная, а общего вида и не симметрична относительно оси Oy и начала координат.
Задача 11.4 [2; стр. 74]. Докажите, что функция является нечетной
y = x2(2x – x3)
Решение
Область определения функции D(f) = (-∞; +∞).
f(-x) = (-x)2(2(-x) – (-x)3) = x2(-2x – (-1)x3) = -x2(2x – x3) = -f(x).
f(-x) = -f(x).
Следовательно функция нечетная на области определения.
Задача. Исследовать функцию на четность, нечетность f(x) = (x + x2)2.
Решение
f(-x) = (-x + (-x)2)2 = (-x + x2)2 ≠ f(x) = (x + x2)2.
f(-x) = (-x + x2)2 ≠ -f(x) = -(x + x2)2.
Заданная функция ни четная, ни нечетная, а общего вида.
Арифметической прогрессией называется числовая последовательность, каждый последующий член, которой, начиная со второго, отличается от предыдущего на величину разности арифметической последовательности d.
Арифметическая прогрессия задается рекуррентно:
a1; an = an-1 + d, n > 1
где первый член a1 и разность арифметической прогрессии d – заданны числами.
d - разность между последующим и предыдущим числом:
d = an – an-1 = an+1 – an = a2 - a1.
Запишем в столбик члены арифметической прогрессии
a1;
a2 = a1 + d;
a3 = a2 + d = a1 + 2d;
a4 = a3 + d = a1 + 3d ...
n – ный член арифметической прогрессии определяется по формуле
an = a1 + (n – 1)d
Сумма n членов арифметической прогрессии:
![]()
подставим an = a1 + (n – 1)d
![]()
Задача 16.31 [2; стр. 103].
Сумма второго и пятого членов арифметической прогрессии равна 18, а произведение второго и третьего ее членов равно 21. Запишите первые пять членов этой прогрессии, если известно, что третий ее член - положительное число.
Дано: a2 + a5 = 18; a2a3 = 21; a3 > 0.
Решение
a3 > 0 ⇒ a2 > 0 ⇒ a5 > 0
an = a1 + d(n - 1)
a2 = a1 + d
a3 = a1 + 2d
a5 = a1 + 4d
Подставляем в заданную систему
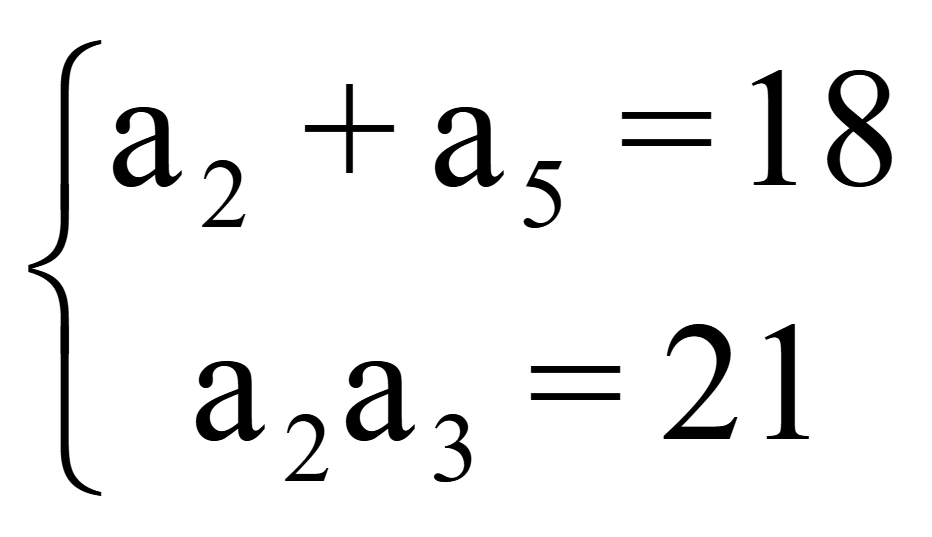
и получаем систему уравнений
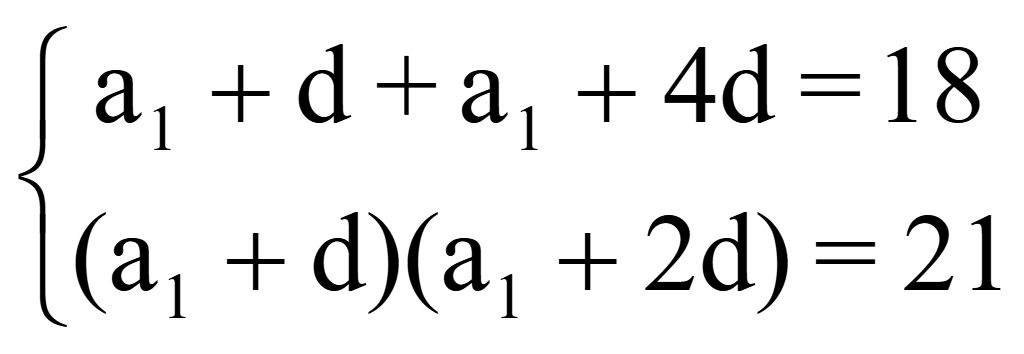
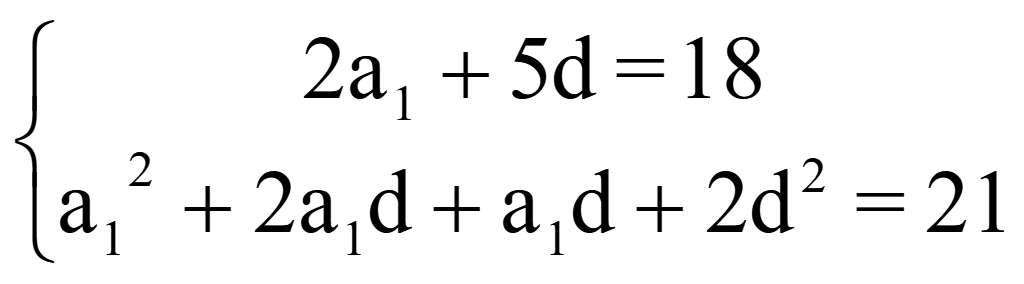
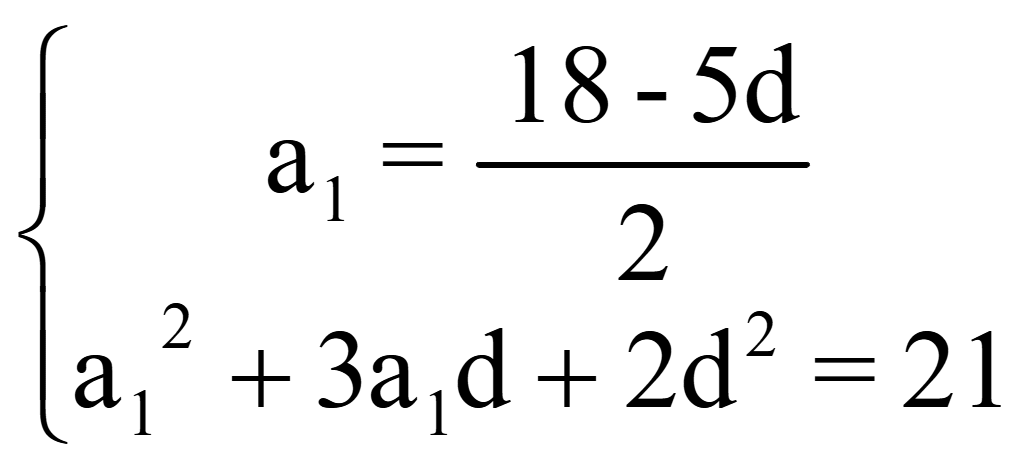
![]()
81 – 45d + 6,25d2 + 27d – 7,5d2 + 2d2 = 21;
0,75d2 – 18d + 81 – 21 = 0;
0,75d2 – 18d + 60 = 0.
Разделим на 0,75, то есть умножим на 4/3
d2 – 24d + 80 = 0.
По теореме Виета
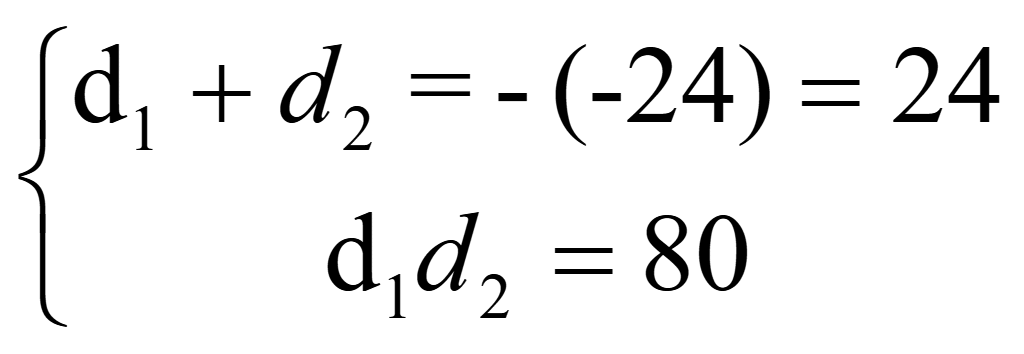
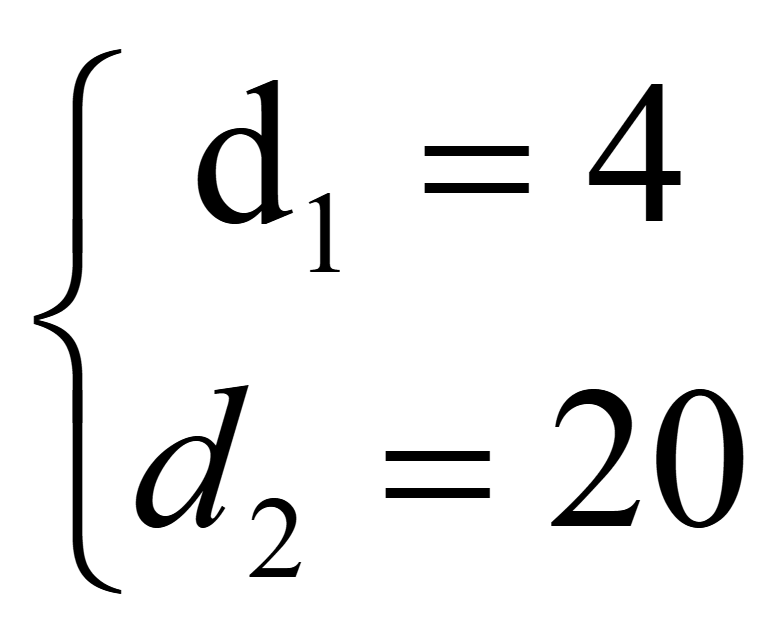
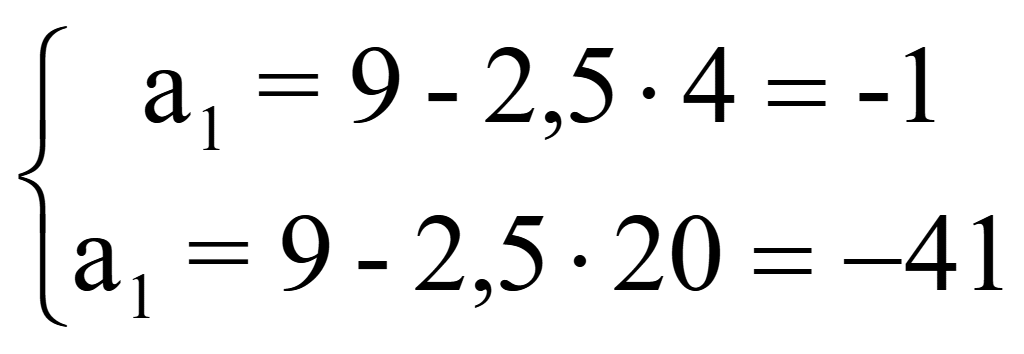
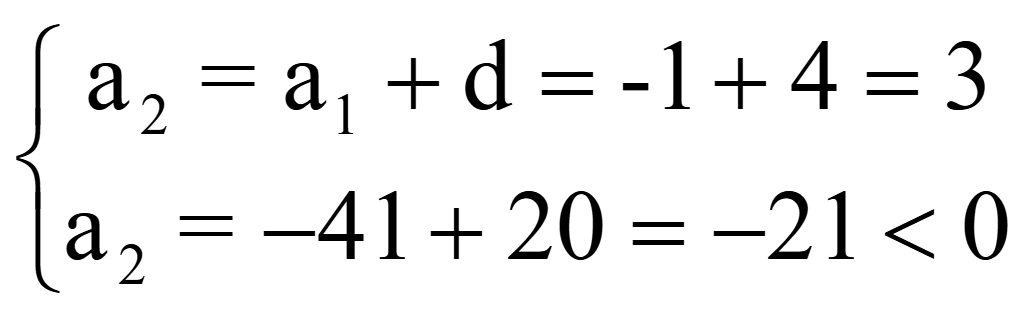
Следовательно, a1 = -1; d = 4; a2 = 3;
a3 = a2 + d = 3 + 4 = 7;
a4 = a3 + d = 7 + 4 = 11;
a5 = a4 + d = 11 + 4 = 15.
Проверка
a2 + a5 = 3 + 15 = 18
a2a3 = 3·7 = 21.
Ответ: a1 = -1; a2 = 3; a3 = 7; a4 = 11; a5 = 15.
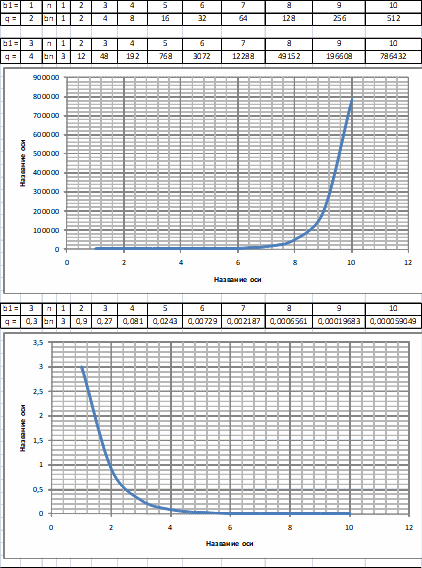
Геометрической прогрессией называется ненулевая числовая последовательность, каждый последующий член, которой, начиная со второго, получается из предыдущего умножением на знаменатель геометрической прогрессии q.
Арифметической (геометрической) прогрессией называется последовательность, каждый последующий член, которой, начиная со второго, отличается от предыдущего на величину разности d (путем умножения на знаменатель q).
b1,
b2 = b1·q,
b3 = b2q = b1·q2,
b4 = b3q = b1·q3,
…,
bn = bn-1q = b1·qn-1,
где q – знаменатель геометрической прогрессии
![]()
Формула общего члена геометрической прогрессии:
bn = b1qn-1
Сумма n членов геометрической прогрессии:
![]()
Логарифм b по основанию a
logab = c,
где a – основание, a > 0, a ≠ 1;
b – подлогарифмическое выражение, b > 0.
Логарифм выражения b по основанию a – это показатель степени, в которую надо возвести основание a, чтобы получить подлогарифмическое выражение b:
ac = b.
Показательная функция и логарифмическая - это взаимообратные функции, поэтому их можно переносить в другую часть равенства, сохраняя основание, но меняя одну функцию на другую
logab = c
b = ac.
Запомнить это помогает мысленное вписывание прямо в логарифм ac = b:
![]() .
.
При нахождении логарифма задумываешься, в какую степень надо возвести основание, чтобы получить подлогарифмическое выражение. a, b и c могут быть сложными выражениями.
Если в выражение ac = b подставить c = logab, то получим
![]()
Если основание число e, то получаем натуральный логарифм
![]() .
.
Если основание 10, то получаем десятичный логарифм
![]() .
.
![]()
![]()
![]() ;
;
![]() ;
;
![]() .
.
Переход к любому новому основанию
![]() .
(1)
.
(1)
Некоторые компьютерные программы могут вычислять лишь натуральный логарифм, поэтому при вычислении логарифма с любым основанием приходится переходить к основанию e (к натуральным логарифмам):
![]() ;
;
Если надо вычислить log23, то компьютерная программа может выглядеть так:
b=3
a=2
c=ln(b)/ln(a)
Переменная c содержит значение log23.
![]() .
.
Помножив
обе части уравнения (1) на знаменатель
![]() получим
получим
![]() .
.
![]() ;
;
![]() .
.
![]() ;
;
при перемножении логарифмов можно менять между логарифмами основания или подлогарифмические выражения, это может упростить задачу нахождения логарифмов:
![]() .
.
![]()
![]()
Логарифм произведения равен сумме логарифмов:
![]()
Логарифм частного равен разности логарифмов
![]()
Степени
![]()
![]()
![]()
![]()
![]()
![]()
logab-1 = -logab
![]()
loga-1b = -logab
Сравнение логарифмов
Если основания логарифмов равны и больше 1, то подлогарифмические выражения и логарифмы изменяются одинаково и мы можем перейти от логарифмов к сравнению подлогарифмических выражений, сохраняя прежний знак неравенства.
logab > logac,
где a > 1, то
b > c.
Если дано неравенство
![]() ,
,
где a > 1, то
logab < logac,
так как a > 1, то при сравнении подлогарифмических выражений знак неравенства сохраняется
b < c.
Если дано неравенство
logab > -logac
где a > 1, то
logab > logac-1;
так как a > 1, то при сравнении подлогарифмических выражений знак неравенства сохраняется
b > c-1;
![]()
Если основания логарифмов равны и меньше 1, но больше 0, то подлогарифмические выражения и логарифмы изменяются в обратном порядке и мы можем перейти от логарифмов к сравнению подлогарифмических выражений, изменяя знак неравенства на противоположный.
logab > logac,
где 0 < a < 1, то
b < c.
Если дано неравенство
![]()
где 0 < a < 1, то, избавляясь от дробей меняется знак неравенства
logab < logac,
так как 0 < a < 1, то при сравнении подлогарифмических выражений знак неравенства меняется
b > c.
Пример:
![]()
При a > 1 функция y = logax возрастает
При 0 < a < 1 функция y = logax убывает
Если основание логарифма e, то логарифм называется натуральным:
logex = lnx.
Если основание 10, то получаем десятичный логарифм:
log10x = lgx.
Таблица показательных и обратных им логарифмических функций с основаниями а
Показательная функция |
Логарифмическая функция |
ac = b |
logab = c |
ec = b |
lnb = c |
Функцию можно перенести в другую часть равенства в виде обратной функции
Действие, функция в одной части равенства |
Обратное действие, функция в другой части равенства |
sin φ = b |
φ = (-1)narcsin b + πn, n ϵ Z |
cos φ = b |
φ = ±arccos b + 2πn, n ϵ Z |
tg φ = b |
φ = arctg b + πn, n ϵ Z |
ctg φ = b |
φ = arcctg b + πn, n ϵ Z |
a2n = b |
|
a2n+1 = b |
|
ac = b |
c =logab |
Производная |
Интеграл |
Умножение |
Деление |
Сложение |
Вычитание |
Деление на дробь |
Умножение на эту дробь |
1. Математика ЕГЭ Демо 2013.
2. Алгебра. 9 класс. В 2 ч. Ч.2. Задачник. Мордкович А.Г. и др. 2010. - 223 с.
© 30.05.2021 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru