© 2020 Репетитор Ольшевский Андрей Георгиевич консультирует по авиации, двигателям, искусственному интеллекту, генерации идей, электронике, физике, математике, информатике, программированию, техническим дисциплинам по Скайп da.irk.ru
Сайт super-code.ru наполняется книгами, которые можно скачать бесплатно
Геометрия 7, 8, 9, 10, 11 класс, определения и формулы
Оглавление
Условие существования треугольника 11
Трапеция 11
Теоремы из 7 класса распределить по разделам 12
Сумма углов выпуклого n-угольника 13
Величина угла правильного n-угольника 13
Синус 16
Окружность 16
Дуга окружности измеряется в градусной мере или в радианах, а также характеризуется длиной 16
Теорема о вписанном в окружность угле 16
Признаки подобия треугольников 16
9 класс 18
Лемма о коллинеарных векторах 18
Разложение вектора по двум неколлинеарным векторам 18
Координаты точки по формулам тригонометрии 20
Теорема о площади треугольника 20
Скалярное произведение векторов 23
Физический смысл скалярного произведения векторов 24
Скалярное произведение векторов в координатах 25
Свойства скалярного произведения векторов 26
Площадь треугольника по формуле Герона 26
Сумма углов и угол правильного многоугольника 28
Описанная около правильного многоугольника окружность 29
Окружность, вписанная в правильный многоугольник 29
Площадь, сторона правильного n-угольника 30
Длина дуги с градусной мерой α 31
Площадь сектора с градусной мерой α 31
Отображение плоскости на себя 31
10 класс 32
Стереометрия 32
Следствия из аксиом стереометрии 33
Параллельные прямые в пространстве 33
Параллельность прямой и плоскости 34
7 класс (до 128 с)
Условие существования треугольника
Сторона треугольника меньше суммы двух других сторон.
Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов катетов
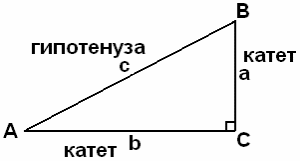
c2 = a2 + b2.
Трапеция
Трапеция – это четырехугольник, у которого две стороны, называемые основаниями, параллельны, а две другие стороны, называемые боковыми сторонами, не параллельны.
Равнобедренная трапеция имеет равные боковые стороны.
Прямоугольная трапеция содержит прямой угол.
Площадь трапеции
Параллелограмм
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны.
Площадь параллелограмма
Прямоугольник
Прямоугольник - это параллелограмм, все углы которого прямые.
Теоремы из 7 класса распределить по разделам
При пересечении параллельных прямых секущей соответственные углы равны.
Теорема. Сумма углов треугольника равна 1800.
Внешний угол треугольника является смежным с внутренним углом треугольника.
Теорема. Внешний угол треугольника равен сумме внутренних углов треугольника, не смежных с этим внешним углом.
8 класс (от 128 до 256 с)
Сумма углов выпуклого n-угольника
У выпуклого n-угольника сумма углов равна (n - 2)·1800.
Если углы α выпуклого n-угольника равны, то их сумма равна nα
nα = (n - 2)·1800.
Величина угла правильного n-угольника
Величина угла α правильного n-угольника
![]()
![]()
![]()
![]()
Определим число сторон правильного n-угольника по известному углу α
1 способ
![]()
![]()
![]()
![]()
![]()
![]()
2 способ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3 способ
Если углы α выпуклого n-угольника равны, то их сумма равна nα
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Синус
Окружность
Дуга окружности измеряется в градусной мере или в радианах, а также характеризуется длиной
Центральный угол
Угол, вершина которого в центре окружности. Величина центрального угла равна величине дуги, на которую он опирается.
Вписанный угол
Вписанным называется угол с вершиной на окружности и сторонами, пересекающими окружность.
Теорема о вписанном в окружность угле
Вписанный угол равен половине центрального угла и дуги, на которую опираются вписанный и центральный углы.
Признаки подобия треугольников
Задача 551 а [Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]
Дано: На стороне CD параллелограмма ABCD отмечена точка E. Прямые AE и BC пересекаются в точке F. Найдите: а) EF и FC, если DE=8 см, EC=4 см, BC=7 см. AE=10 см; б) DE и EC, если AB=8 см, AD=5 см, CF=2 см.
Решение
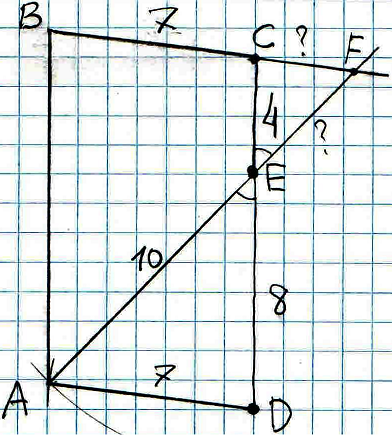
1.Вертикальные углы равны ∠AED = ∠CEF.
2.Накрест лежащие углы равны ∠ADE = ∠FCE.
3.ΔAED ~ ΔCEF по первому признаку подобия (по 2-м углам). Отношения соответствующих сторон подобных треугольников равны
![]()
![]()
Сократим
![]()
![]() (см);
(см);
![]() (см).
(см).
Ответ: EF = 5 см, FC = 3,5 см.
Вписанная окружность
Вписанная окружность касается всех сторон многоугольника, который называется описанным около этой окружности.
Вписать окружность можно в любой треугольник и притом только одну.
Вписать окружность можно не в любой многоугольник.
Вписать окружность можно в выпуклый четырехугольник, суммы противоположных сторон которого равны.
Описанная окружность
Описанная окружность проходит через все вершины многоугольника, который называется вписанным в эту окружность.
9 класс
Коллинеарные векторы
Коллинеарные векторы – это векторы, находящиеся на одной прямой или на параллельных прямых.
Лемма о коллинеарных векторах
![]()
Средняя линия трапеции
Средняя линия трапеции равна полусумме оснований и параллельна основаниям.
Разложение вектора по двум неколлинеарным векторам
Любой
вектор
![]() единственным образом разлагается на плоскости по двум неколлинеарным
данным векторам
единственным образом разлагается на плоскости по двум неколлинеарным
данным векторам
![]() и
и
![]() с единственными коэффициентами разложения x
и y:
с единственными коэффициентами разложения x
и y:
![]()
Разложим
заданный вектор
![]() по заданным неколлинеарным векторам
по заданным неколлинеарным векторам
![]() и
и
![]() :
:
![]()
Проведем из одной точки заданные векторы
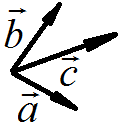
Из
конца вектора
![]() проведем прямые, параллельные векторам
проведем прямые, параллельные векторам
![]() и
и
![]() до пересечения с лучами, сонаправленными с векторами
до пересечения с лучами, сонаправленными с векторами
![]() и
и
![]() .
Получим параллелограмм
.
Получим параллелограмм
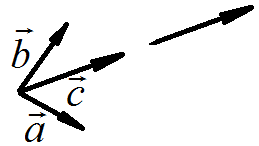
Координаты вектора
Если
вектор
![]() задан точками M1(x1;
y1; z1)
и M2(x2;
y2; z2),
то его координаты
задан точками M1(x1;
y1; z1)
и M2(x2;
y2; z2),
то его координаты
![]()
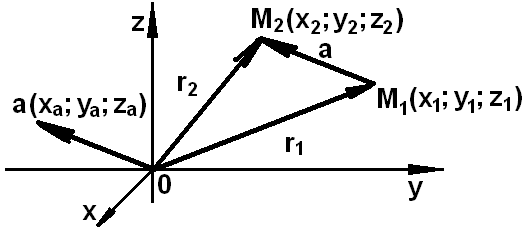
Длина вектора
![]()
![]()
Расстояние между точками M1(x1; y1) и M2(x2; y2)
![]()
Длина вектора
![]()
M1(x1; y1; z1) и M2(x2; y2; z2)
![]()
Координаты точки по формулам тригонометрии
Координаты точки A, находящейся на расстоянии OA от начала координат O
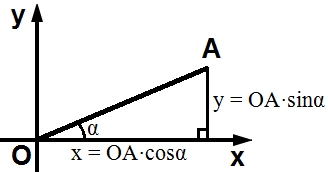
x = OA·cosα
y = OA·sinα
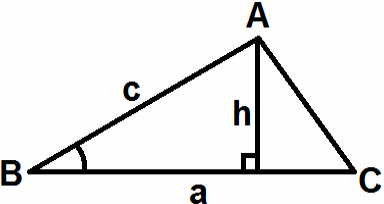
Теорема о площади треугольника
Площадь треугольника
![]()
В прямоугольном треугольнике
h = c·sinB
![]()
Площадь треугольника равна половине произведения двух сторон треугольника на синус угла между ними.
![]()
Теорема синусов
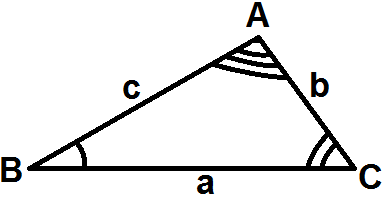
Стороны треугольника пропорциональны синусам противоположных углов
![]()
Отношение стороны треугольника к синусу противоположного угла равно диаметру описанной окружности
![]()
Теорема косинусов
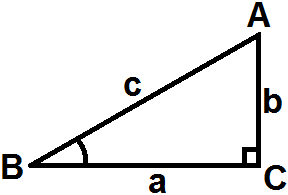
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов
c2 = a2 + b2.
Рассмотрим произвольный треугольник
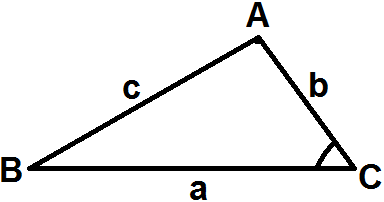
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
c2 = a2 + b2 – 2ab·cosC.
При C = 900 cos 900 = 0, получаем
c2 = a2 + b2
в соответствии с теоремой Пифагора, поэтому теорему косинусов называют обобщенной теоремой Пифагора.
Решение треугольников
Решение треугольника – это нахождение по трем данным элементам остальных трех элементов, определяющих треугольник (трех сторон и трех углов). Трех заданных углов не достаточно для решения треугольника, потому что размер треугольника в этом случае может быть любым. При решении треугольника могут использоваться теоремы косинусов, синусов и возможность определения третьего угла путем вычитания из 1800 двух известных углов.
Попарно приравнивая элементы из теоремы синусов
![]()
можно определить неизвестный элемент по трем известным. Например, приравняв
![]()
можно определить
![]()
или
![]()
Из теоремы косинусов
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Из формулы суммы углов треугольника
∠A + ∠B + ∠C = 1800
можно найти любой угол по известным двум другим.
Угол между векторами
Угол между векторами – равен углу между проведенными из одной точки лучами, сонаправленными с этими векторами. Угол между сонаправленными векторами равен 00. Угол между перпендикулярными векторами равен 900.
Скалярное произведение векторов
Скалярное произведение двух векторов – это произведение длин векторов на косинус угла между ними
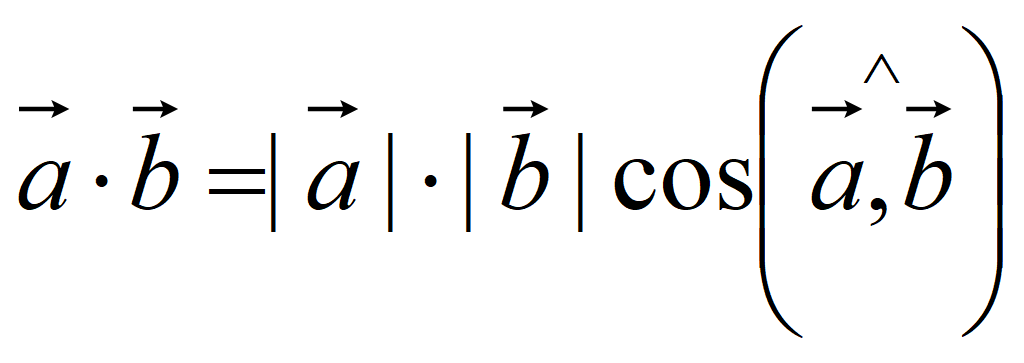
Если
ненулевые векторы перпендикулярны, то их скалярное произведение равно
нулю
![]() .
Так как cos900 = 0.
.
Так как cos900 = 0.
Если
![]() ,
то
,
то
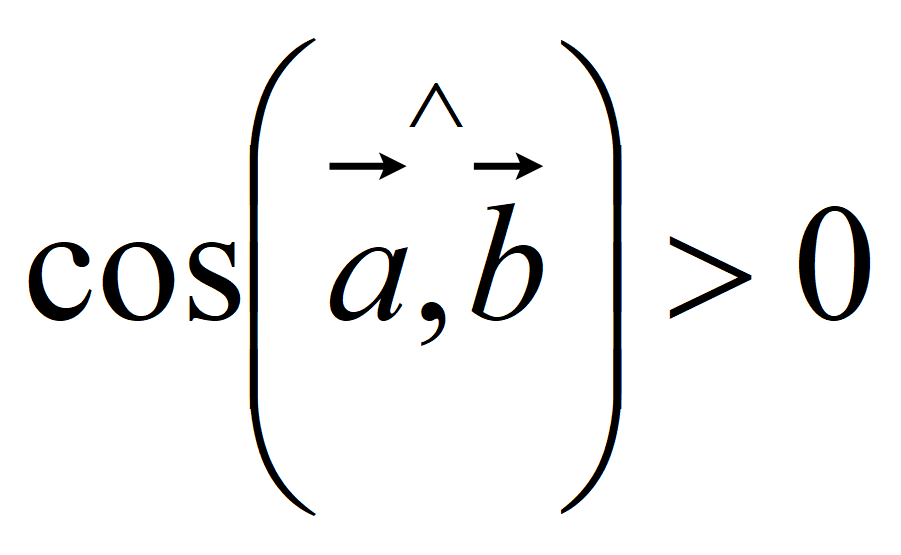 ,
следовательно
,
следовательно
![]() .
При уменьшении угла между векторами
.
При уменьшении угла между векторами
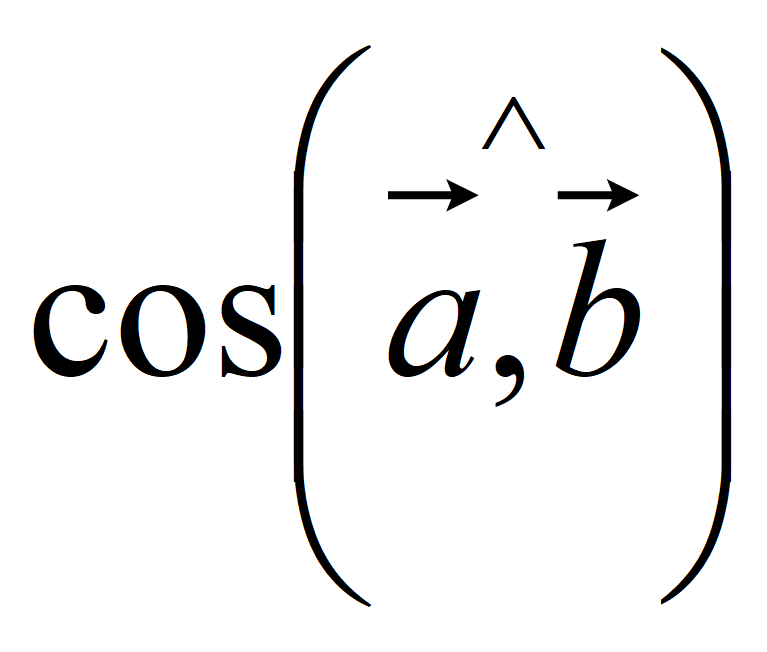 возрастает и достигает максимального значения при
возрастает и достигает максимального значения при
![]() =
00, то есть при сонаправленности векторов
=
00, то есть при сонаправленности векторов
![]() .
Так как cos00 = 1, то
.
Так как cos00 = 1, то
![]() .
.
Если
![]() ,
то
,
то
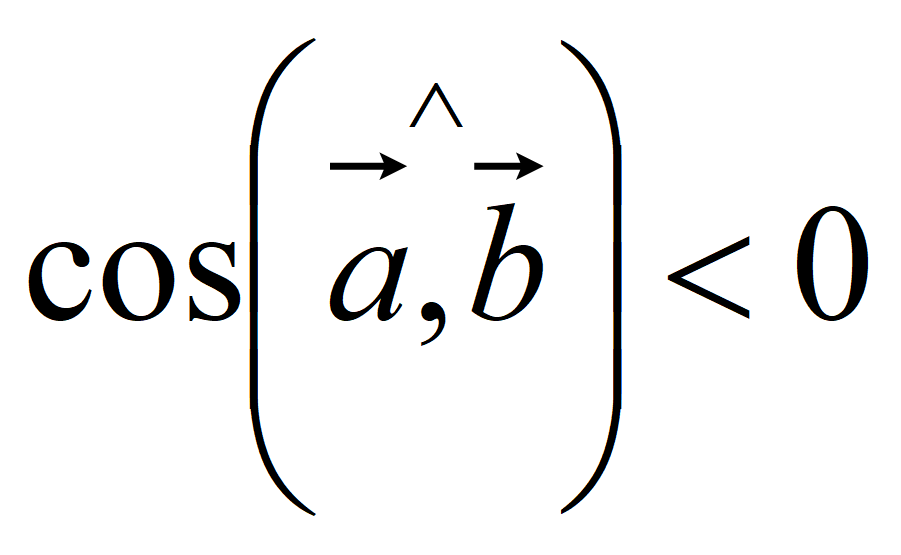 ,
следовательно
,
следовательно
![]() .
При увеличении угла между векторами
.
При увеличении угла между векторами
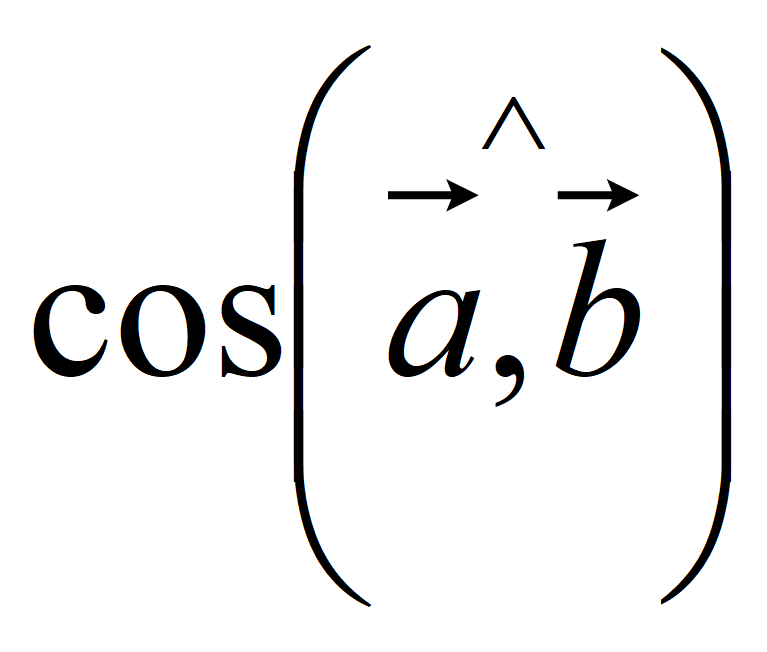 уменьшается и достигает минимального значения при
уменьшается и достигает минимального значения при
![]() =
1800, когда векторы противоположно направлены
=
1800, когда векторы противоположно направлены
![]() .
Так как cos1800 = -1, то
.
Так как cos1800 = -1, то
![]() .
.
Скалярный квадрат вектора
![]()
Физический смысл скалярного произведения векторов
Из
курса физики известно, что работа A силы
![]() при перемещении тела
при перемещении тела
![]() равна произведению длин векторов силы
равна произведению длин векторов силы
![]() и перемещения
и перемещения
![]() на косинус угла между ними, то есть равна скалярному произведению
векторов силы и перемещения
на косинус угла между ними, то есть равна скалярному произведению
векторов силы и перемещения
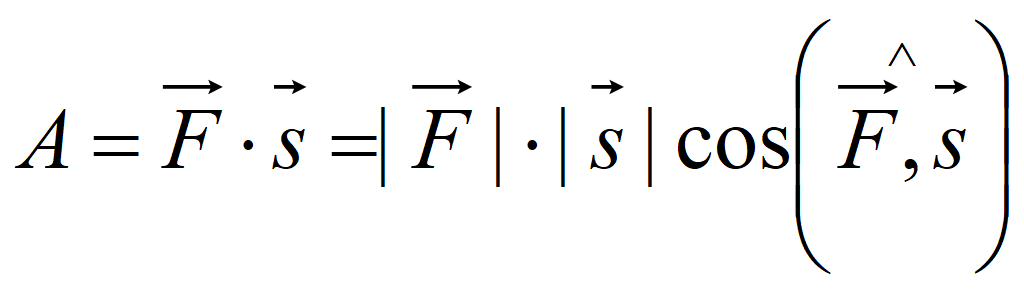
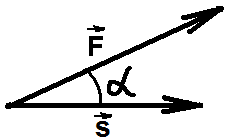
Если
![]() < 900, то работа силы
< 900, то работа силы
![]() на перемещении
на перемещении
![]() положительна A > 0.
положительна A > 0.
Если
![]() = 900, то работа силы
= 900, то работа силы
![]() на перемещении
на перемещении
![]() равна нулю A = 0.
равна нулю A = 0.
Если
![]() > 900, то работа силы
> 900, то работа силы
![]() на перемещении
на перемещении
![]() отрицательна A < 0.
отрицательна A < 0.
Задача. Определить работу силы тяжести при подъеме легкового автомобиля массой 1 тонна по трассе длинной 1 км, имеющей угол наклона 300 к горизонту. Сколько литров воды при температуре 200 можно вскипятить, используя эту энергию?
Скалярное произведение векторов в координатах
Скалярное
произведение векторов
![]() и
и
![]() в прямоугольной системе координат
в прямоугольной системе координат
![]()
![]()
Угол между векторами
Если
ненулевые векторы
![]() и
и
![]() перпендикулярны, то их скалярное произведение равно нулю
перпендикулярны, то их скалярное произведение равно нулю
![]() ,
,
![]() =
0.
=
0.
Косинус угла между ненулевыми векторами
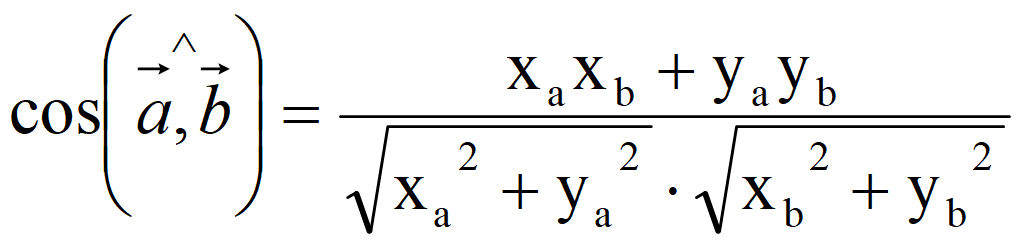
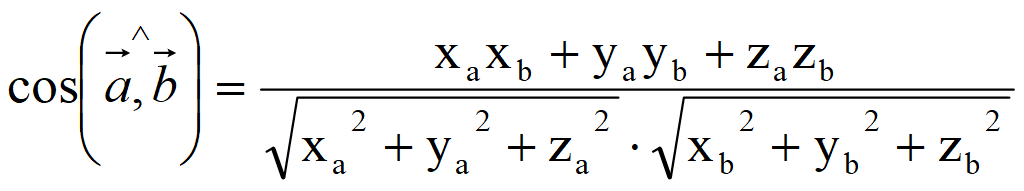
Свойства скалярного произведения векторов
Свойства
скалярного произведения справедливы при любых
![]() ,
,
![]() ,
,
![]() ,
k:
,
k:
1.
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
.
2.Переместительный
закон
![]()
3.Распределительный
закон
![]()
4.Сочетательный
закон
![]()
Площадь треугольника по формуле Герона
Формула Герона
![]() ,
,
где полупериметр p определяется по формуле
![]()
a, b, c – стороны треугольника.
Площадь треугольника
SΔ = pr,
где r – радиус вписанной в треугольник окружности.
Площадь треугольника
![]()
где R – радиус описанной около треугольника окружности.
Из формул площади треугольника
![]()
и равенства, содержащего теорему синусов
![]()
можно определить неизвестную величину по заданным величинам.
Задача. По трем сторонам треугольника a, b, c определить три угла, радиусы вписанной r и описанной R окружностей.
Решение
Определяем полупериметр
![]()
По формуле Герона определяем площадь
![]() ,
,
Из формулы площади треугольника
SΔ = pr
определяем радиус вписанной окружности
![]()
Из формулы площади треугольника
![]()
определяем радиус описанной окружности
![]()
Из теоремы косинусов можем определить косинусы всех трех углов. Или используя теорему синусов
![]()
можем найти синусы углов
Подставив
![]() ,
,
получаем
![]()
![]()
![]()
![]()
![]()
Правильный многоугольник
Правильный многоугольник – это выпуклый многоугольник, у которого равны все углы, а также стороны.
Сумма углов и угол правильного многоугольника
Сумма углов правильного n-угольника
nαn = (n – 2)·1800.
Отсюда угол правильного n-угольника
![]()
![]()
Получаем прогрессию суммы углов правильных n-угольников
3α3 = (3 – 2)·1800 = 1·1800 = 1800.
4α4 = (4 – 2)·1800 = 2·1800 = 3600 = 3α3 + 1800 = 1800 + 1800 = 3600.
5α5 = (5 – 2)·1800 = 3·1800 = 5400 = 4α4 + 1800 = 3600 + 1800 = 5400.
6α6 = (6 – 2)·1800 = 4·1800 = 7200 = 5α5 + 1800 = 5400 + 1800 = 7200.
nαn = (n-1)αn-1 + 1800.
Sn = Sn-1 + 1800.
Арифметическая прогрессия, в которой первый член является суммой углов правильного 3-ка
S3 = 3α3 = 1800.
Разность
d = 1800.
Sn = Sn-1 + 1800.
Sn = nαn = (n – 2)·1800.
Суммы углов правильных n-угольников
3α3 = 1800.
4α4 = 1800 + 1800 = 3600.
5α5 = 3600 + 1800 = 5400.
6α6 = 5400 + 1800 = 7200.
7α7 = 7200 + 1800 = 9000.
Описанная около правильного многоугольника окружность
Окружность, описанная около многоугольника – это окружность, на которой лежат все вершины многоугольника.
Только одна окружность описывает правильный многоугольник.
Окружность, вписанная в правильный многоугольник
Окружность, вписанная в многоугольник – это окружность, касающаяся всех сторон многоугольника.
Только одну окружность можно вписать в правильный многоугольник.
Центры описанной и вписанной окружностей совпадают с центром правильного многоугольника.
Площадь, сторона правильного n-угольника
![]()
где P – периметр правильного многоугольника;
r – радиус вписанной окружности.
P = nan,
где an – сторона правильного n-угольника.
![]() ,
,
где S∆ – площадь одного из n равных треугольников, образующихся при соединении центра правильного n-угольника с его вершинами.
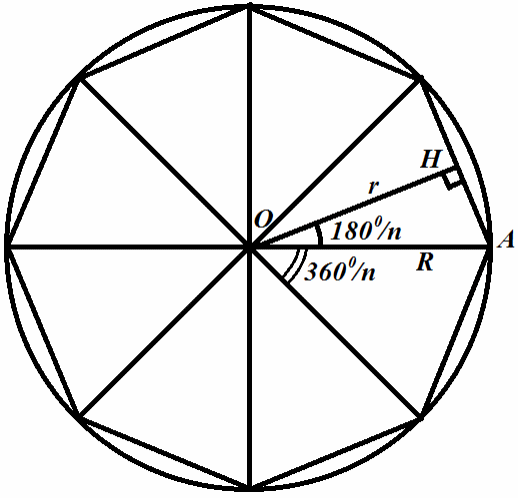
Сторона правильного n-угольника.
![]() ,
,
где R – радиус описанной окружности.
![]()
Длина окружности
![]()
Длина дуги с градусной мерой α
![]()
Площадь круга
![]()
Площадь сектора с градусной мерой α
![]()
Отображение плоскости на себя
Отображение плоскости на себя – это сопоставление каждой точке плоскости какой-то точке этой же плоскости.
Осевая симметрия является отображением плоскости на себя.
Движение плоскости
Движение плоскости – это сохраняющее расстояния отображение плоскости на себя.
Осевая симметрия является движением плоскости. Центральная симметрия плоскости является движением плоскости.
Теорема: «При движении отрезок отображается на равный ему отрезок».
Следствие: «При движении фигура отображается на равную ей фигуру».
Наложение является отображением плоскости на себя, при этом различные точки плоскости отображаются также в различные точки с сохранением расстояний.
Все наложения являются движением плоскости.
Теорема: «Все движения являются наложением».
Следствие: «При движении произвольная фигура отображается на равную ей фигуру».
Параллельный
перенос на вектор
![]() - это отображение плоскости на себя, при котором каждая точка
плоскости отображается в точку на вектор
- это отображение плоскости на себя, при котором каждая точка
плоскости отображается в точку на вектор
![]() .
.
Любой параллельный перенос является движением.
Поворотом плоскости вокруг заданной точки на данный угол называется отображение плоскости на себя, при котором любая точка в результате вращения вокруг заданной точки на данный угол отображается в точку.
Любой поворот является движением.
10 класс
Стереометрия
Стереометрия - раздел геометрии, изучающий фигуры в пространстве.
Основные фигур стереометрии: точки, прямые, плоскость.
Многогранники - геометрические тела с поверхностями, выстроенными из многоугольников.
Аксиомы стереометрии
Аксиома 1: через 3 точки, не принадлежащие одной прямой, проходит единственная плоскость.
Аксиома 2: Если в плоскости лежат 2 точки прямой, то прямая и все ее точки лежат в данной плоскости, то есть через прямую проходит данная плоскость.
Прямая и плоскость пересекаются в одной общей точке.
Аксиома 3: Если 2 плоскости пересекаются в общей точке, то они пересекаются и в общей прямой, содержащей все общие точки данных плоскостей, то есть плоскости пересекаются в прямой.
Следствия из аксиом стереометрии
Теорема: через прямую и не принадлежащую ей точку проходит единственная плоскость.
Теорема: через пару пересекающихся прямых проходит единственная плоскость.
Параллельные прямые в пространстве
Параллельными называются две не пересекающиеся прямые в пространстве, лежащие в одной плоскости.
Через точку, не принадлежащую данной прямой, проходит единственная прямая, параллельная данной прямой на плоскости и в пространстве.
Параллельность трех прямых
Если данную плоскость пересекает одна из двух параллельных прямых, то и вторая прямая пересекает данную плоскость.
Если прямые параллельны данной прямой, то все прямые параллельны.
Параллельность прямой и плоскости
Прямая и плоскость
Параллельными называются прямая и плоскость, не имеющие общих точек.
Если не принадлежащая данной плоскости прямая параллельна какой-то прямой, принадлежащей этой плоскости, то данные прямая и плоскость параллельны.
Если через данные параллельные прямую и плоскость проходит плоскость, содержащая данная прямую, то эта плоскость пересекает данную плоскость по прямой, параллельной данной прямой.
Угол между прямой и плоскостью
Угол между прямой и плоскостью равен 900, если прямая перпендикулярна плоскости или углу между прямой и ее проекцией на плоскость. Если прямая параллельна плоскости, то угол между ними равен 00.
Скрещивающиеся прямые
Скрещивающимися называются прямые, не лежащие в одной плоскости.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся [Геометрия. 10-11 классы : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.; стр. 15].
Три случая расположения двух прямых в пространстве:
1)прямые пересекаются в одной общей точке, поэтому лежат в одной плоскости;
2)прямые параллельны, поэтому не пересекаются и лежат в одной плоскости;
3)прямые скрещиваются, поэтому не пересекаются и не лежат в одной плоскости.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна [Л.С. Атанасян. Геометрия. 10-11 классы; стр. 16].
Правильная призма
Правильной называется прямая призма с основаниями - правильными многоугольниками.
Опубликовано 12.05.17
© 2023 Ольшевский Андрей Георгиевич, сайт super-code.ru, e-mail: da.irk.ru@mail.ru