© 2021 Ольшевский Андрей Георгиевич репетитор по аэродинамике, авиации, физике, математике, информатике, двигателям, искусственному интеллекту, генерации идей, электронике, программированию, техническим дисциплинам по Скайп da.irk.ru
Сайт super-code.ru наполняется книгами, вы можете книги скачать
Аэродинамика
Оглавление
1 Вязкость воздуха. Пограничный слой 3
2 Несжимаемая, сжимаемая жидкость 7
5 Скоростная система координат 14
Репетитор по аэродинамике, математике, информатике, физике, техническим дисциплинам
8 Сужение 15
9 Действия пилота при отскоке самолета от земли после грубой посадки 15
Перечень условных обозначений, символов, единиц и терминов 17
Список использованных источников 18
Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru 19
При обтекании поверхности набегающим потоком воздуха со скоростью V вблизи от этой поверхности скорость частиц воздуха уменьшается вплоть до полного торможения частиц, непосредственно контактирующих с неровностями поверхности (см. рисунок 1 [1]). Разделим условно поток по вертикали к поверхности на отдельные слои. В этом случае слой, находящийся ближе к поверхности будет двигаться с меньшей скоростью, чем смежный с ним слой, расположенный выше. Нижний слой будет оказывать сопротивление верхнему слою. В этом явлении проявляется вязкость воздуха, т. е. его способность сопротивляться смещению слоев, их относительному перемещению, вызванная силами внутреннего трения. Вязкость не проявляется при отсутствии взаимного перемещения слоев воздуха.

Рисунок 1 — Пограничный слой
Пограничный слой — это слой воздуха вблизи обтекаемой поверхности, в котором проявляется его вязкость и происходит увеличение скорости от 0 до скорости обтекающего невозмущенного потока.
На носке обтекаемого тела толщина пограничного слоя минимальна и возрастает вдоль потока (см. рисунок 2 [1]). Толщина пограничного слоя в несколько раз меньше характерного линейного размера обтекаемого тела (у поверхности самолета от нескольких миллиметров до нескольких сантиметров).
Рисунок 2 — Обтекание тела газом (толщина пограничного слоя демонстративно увеличена)
Касательные напряжения, возникающие в пограничном слое
![]() (1)
(1)
μ — коэффициент динамической вязкости, Па·с,
![]() -
градиент скорости.
-
градиент скорости.
При увеличении температуры возрастает скорость хаотического теплового движения молекул, поэтому возрастает динамическая вязкость воздуха.
Коэффициент кинематической вязкости воздуха, м2/с
![]() (2)
(2)
отсюда коэффициент динамической вязкости
μ = νρ (3)
Коэффициент кинематической вязкости возрастает одновременно с высотой полета.
Из-за градиента скорости в пограничном слое частицы начинают вращаться тем сильнее, чем больше градиент скорости, то есть чем ближе к обтекаемой поверхности. Поэтому пограничный слой абсолютно всегда завихрен и называется слоем поверхностного завихрения.
При небольшой скорости набегающего потока или небольшой длине обтекаемой поверхности слои газа в пограничном слое не смешиваются, образуя ламинарный пограничный слой.
При увеличении скорости или длины обтекаемой поверхности слои газа начинают энергично перемешиваться между собой, весь пограничный слой беспорядочно завихряется, образуя турбулентный слой. Толщина турбулентного слоя значительно больше, чем ламинарного. Требуется много энергии на перемещение струек газа во всех направлениях, поэтому сопротивление потока газа в турбулентном слое увеличивается.
Чем больше градиент скорости, тем больше касательные напряжения, возникающие в пограничном слое, и сопротивление движению поверхности относительно воздуха. При турбулентном обтекании градиент скорости у поверхности значительно выше и, поэтому, сопротивление так же значительно выше, чем при ламинарном обтекании. Структура пограничного слоя показана на рисунке 3 [2].
Рисунок 3 — Структура пограничного слоя:1 — ламинарный пограничный слой, 2 — переходный; 3 — турбулентный; 4 – ламинарный подслой: x – координата точки перехода ламинарного слоя в турбулентный
При определенных условиях может возникнуть отрицательный градиент скорости, возникает срыв потока, например при околокритических углах атаки. При срыве потока давление на крыло сверху возрастает, поэтому крыло теряет свои несущие свойства.
Так как скорость при турбулентном обтекании у поверхности нарастает быстрее, то и срыв потока может произойти значительно позже, чем при ламинарном обтекании. Поэтому на крылья применяют турбулизаторы, вызывающие переход ламинарного пограничного слоя в турбулентный.
Точка перехода ламинарного пограничного слоя в турбулентный определяется числом Рейнольдса
![]() (4)
(4)
где l – линейный (вдоль потока) размер, м.
Подставим коэффициент кинематической вязкости
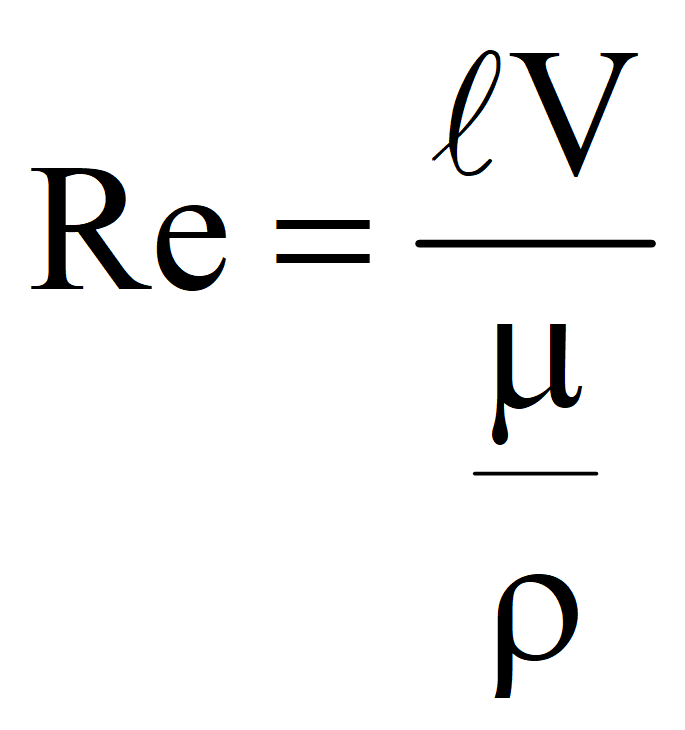 (5)
(5)
![]() (6)
(6)
Критическим числом Рейнольдса называется такое Reкр при котором пограничный слой переходит из ламинарного пограничного слоя в турбулентный. Оно примерно равно
Reкр = 105.
Критическая скорость — это скорость при которой в данных условиях происходит переход условий обтекания в пограничном слое из ламинарного в турбулентный.
Вопрос: при увеличении угла атаки куда смещается точка перехода из ламинарного в турбулентный к носку крыла или к хвостику?
Ответ: При увеличении угла атаки возрастает верхняя обтекаемая длина профиля, поэтому возрастает скорость и Re, поэтому точка перехода из ламинарного в турбулентный смещается ближе к носку крыла, предотвращая тем самым срыв потока до какой-то степени.
При малых скоростях (M < 0,3) воздух принимается несжимаемой жидкостью, т. е. плотность не изменяется (ρ = const). При скоростях близких к скорости Маха воздух сжимается, поэтому давление увеличивается (ρ ≠ const), воздух принимается сжимаемой жидкостью.
![]() ,
(7)
,
(7)
где V – скорость полета, м/с;
a – скорость звука на данной высоте, м/с.
С ростом высоты полета скорость звука уменьшается, а число Маха возрастает.
По таблице стандартной атмосферы скорость звука на нулевой высоте
a = 340,294 м/с = 340,294*3,6 км/ч = 1225,0584 км/ч.
При M = 1 возникает волновой кризис и скорость на нулевой высоте
V = 1225,0584 км/ч.
На высоте 10000 м скорость звука становится равной
a = 299,532 м/с = 299,532*3,6 км/ч = 1078,3152 км/ч.
Критическое число Мкр — это такое M∞, при котором на поверхности летательного аппарата возникают местные скорости потока равные скорости звука, то есть возникают местные скачки уплотнения. Мкр ≤ 1.
В аэродинамике при изучении движения воздуха иногда удобнее использовать не модель сплошной среды, а модель, рассматривающую среду как совокупность множества частиц. В этой модели движение частиц представляют в виде траекторий и линий тока [1], которые совпадают при установившемся движении. Установившимся называется движение, при котором в фиксированной точке вектор скорости не изменяется по величине и направлению с течением времени.
Линия тока — это линия, в каждой точке которой вектор скорости частицы направлен по касательной к этой линии (см. рисунок 4 [1]).
Рисунок 4 — Линия тока и траектория частицы, совпадающие при установившемся движении
В плоскости, перпендикулярной линии тока, проведем замкнутую линию. Через множество точек этой линии проведем бесконечно много линий тока, образующих замкнутую поверхность — трубку тока. Скорости частиц направлены по касательной к линиям тока и к поверхности трубки тока, поэтому частицы не пересекают поверхность и не покидают трубку тока. Частицы, движущиеся в трубке тока, образуют струйку. Струйка называется элементарной, если ее поперечное сечение настолько мало, что можно считать равными скорости частиц в этом сечении в каждый фиксированный момент времени. Рассмотрим элементарную струйку (см. рисунок 5 [1]).
Рисунок 5 — Элементарная струйка
Поскольку поверхность трубки тока непроницаема для частиц воздуха, то при установившемся течении через каждое поперечное сечение элементарной струйки в единицу времени будет протекать одна и та же масса воздуха. Это вытекает из закона сохранения массы, если принять, что трубка тока не имеет разрывов, через которые может поступать или уходить воздух. Поэтому формула, описывающая это явление, называется уравнением неразрывности
m = ρVF = const, (8)
где m – масса воздуха, протекающего через поперечное сечение струйки в единицу времени, кг/с;
ρ – плотность воздуха в данном сечении струйки, кг/м3;
V – скорость воздуха в данном сечении струйки, м/с;
F – площадь поперечного сечения струйки, м2.
Для малых скоростей течения (при М < 0,3) можно принять, что воздух несжимаем, т.е. плотность воздуха не меняется от сечения к сечению (ρ = const). Тогда ее можно исключить из уравнения (8) и, возвращаясь к рисунку 2, записать:
VF = const. (9)
V1F1 = V2F2. (10)
Из этого уравнения можно сделать важный вывод: при уменьшении площади поперечного сечения струйки скорость течения воздуха в ней возрастает, а при увеличении – падает. Но это справедливо только для дозвуковых течений (М < 1).
Важное место в аэродинамике отводится также закону сохранения энергии, который используется для получения взаимосвязи давления и скорости воздуха в струе. На рисунке 6 [1] показана элементарная струйка на виде сбоку.
Рисунок 6 — Движение воздуха в струйке
Рассмотрим относительно некоторого уровня баланс энергии масс воздуха, проходящих через сечения 1 и 2 за одинаковый промежуток времени Δt. Движение воздуха в струйке будем считать установившимся, а сжимаемость и трение учитывать не будем. Выделим для рассмотрения некоторую массу воздуха m, проходящую через сечение 1 со скоростью V1 за время Δt. Эта масса обладает кинетической энергией, равной
![]() (11)
(11)
и имеет потенциальную энергию, равную потенциальной работе силы тяжести mgh1 и силы давления воздуха p1F1 левее сечения 1. Потенциальная работа силы давления равна произведению силы на перемещение, которое равно произведения скорости V1 на промежуток времени Δt, в течение которого рассматриваемая масса воздуха проходит через сечение 1. Потенциальная энергия в сечении 1
EП1 = mgh1 + p1F1V1Δt. (12)
Если не учитывать потери, то по закону сохранения энергии суммарная энергия рассматриваемой массы воздуха при прохождении ею сечения 2 не изменится, поэтому можно записать:
E1 = E2; (13)
EП1 + EК1 = EП2 + EК2; (14)
![]() (15)
(15)
В соответствии с уравнением (10) объем воздуха, проходящий через сечение 1 должен быть равен объему воздуха, проходящего через сечение 2:
V1 = V2; (16)
F1V1Δt = F2V2Δt. (17)
Поделим уравнение (15) на уравнение (17) и получим:
![]() (18)
(18)
![]() (19)
(19)
Мы получили уравнение Бернулли для газа без учета сжимаемости. Если пренебречь действием силы тяжести или предположить, что движение воздуха происходит в горизонтальной плоскости, то потенциальная энергия рассматриваемой массы воздуха не изменится, и из выражения (19) произведение ρgh можно исключить:
![]() (20)
(20)
Слагаемое
p называется статическим давлением, а слагаемое
![]() динамическим давлением или скоростным напором. Сумма же статического
и динамического давлений называется полным давлением и обозначается
p0:
динамическим давлением или скоростным напором. Сумма же статического
и динамического давлений называется полным давлением и обозначается
p0:
![]() (21)
(21)
При внимательном рассмотрении уравнения Бернулли можно заметить, что при увеличении скорости потока динамическое давление будет расти, а статическое соответственно – падать, т.к. их сумма изменяться не должна. Так, при обтекании тела набегающим потоком воздуха (см. рисунок 7 [1]) на его носке существует точка А (критическая точка), в которой скорость потока из-за полного торможения равна 0. В этой точке динамическая составляющая равна нулю, а статическое давление максимально и равно полному давлению. В любой другой точке поверхности тела скорость потока будет больше 0, а это значит, что статическое давление будет меньше, чем в критической точке.

Рисунок 7 — Обтекание тела набегающим потоком
Увеличение скорости дозвукового потока происходит при уменьшении площади поперечного сечения потока и сопровождается уменьшением статического давления.
Взаимосвязь статического и динамического давлений хорошо иллюстрируется на примере функционирования прибора, который носит название трубка Пито-Прандтля, или в технике – приемник воздушного давления (ПВД). Этот прибор широко используется в авиации для определения скорости полета. Схематично трубка Пито – Прандтля изображена на рисунке 8 [1]. Прибор имеет две полости, соединенных с манометром. Когда трубка выставлена вдоль вектора скорости набегающего потока, то в полости 1 давление воздуха будет равно полному давлению, т.к. это критическая точка и поток в ней полностью тормозится. Полость 2 сообщается с потоком через боковое отверстие в трубке, при этом линии тока проходят мимо этого отверстия, не искажаясь. За счет этого в полости 2 действует только статическое давление, а влияние динамического давления исключено. Разность давлений в полостях 1 и 2, измеряемая с помощью манометра, будет равна скоростному напору:
![]() (22)
(22)
Отсюда, зная плотность воздуха, легко определить скорость набегающего потока (или скорость полета).
Рисунок 8 — Схема трубки Пито-Прандтля
![]()
![]()
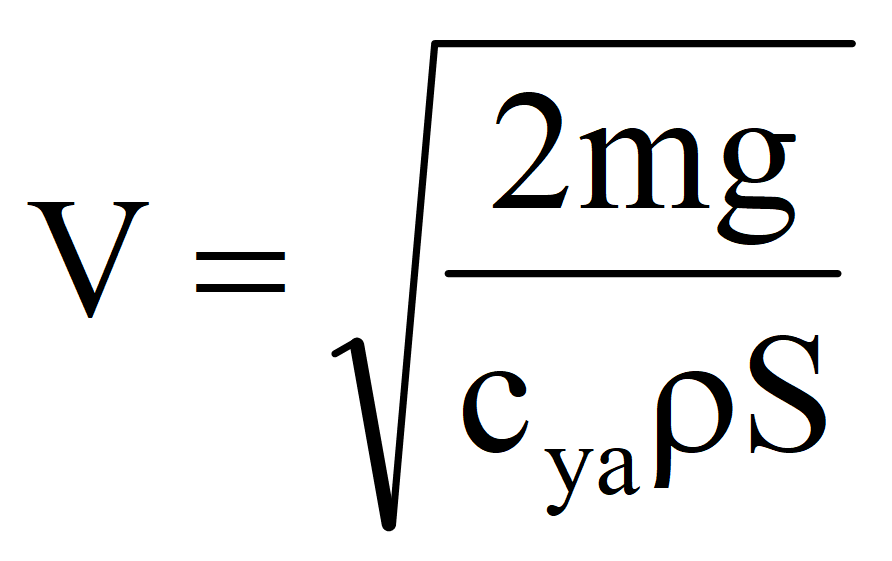
С подъемом на высоту плотность воздуха уменьшается, поэтому требуется большая скорость полета и минимальная скорость увеличивается.
С увеличением высоты максимальная скорость уменьшается. При достижении теоретического потолка минимальная и максимальная скорости становятся равными.
Скоростная система координат имеет нижние индексы a OXaYaZa. На рисунке ниже показаны знаки подъемной силы Ya для различных профилей в зависимости от направления скорости потока (угла атаки). Угол атаки — это угол между хордой крыла и вектором скорости потока.
Фокус - точка, относительно которой не изменяется аэродинамический момент при изменении угла атаки. Различают фокус крыла и фокус самолета. Фокус крыла — точка, относительно которой не изменяется аэродинамический момент, действующий на крыло при изменении угла атаки. Фокус самолета — точка, относительно которой не изменяется аэродинамический момент, действующий на самолет при изменении угла атаки.
При увеличении скорости полета в потоке, окружающем самолет возникают участки, в которых скорость становится равной скорости звука на данной высоте полета. Это вызывает появление местных скачков уплотнения и как следствие значительный рост сопротивления.
Для уменьшения скорости на крыле применяют стреловидность
![]()
Если при грубой посадке самолет отскочил от взлетно-посадочной полосы и угол атаки не достиг критического значения, то нельзя опускать нос самолета, отдавая штурвал (ручку или джойстик) от себя. Перед посадкой двигатели работают на малых оборотах, поэтому горизонтальная скорость, как правило, уже снижена, а после отскока она становится еще меньше. Уменьшение скорости полета V приводит к уменьшению подъемной силы Ya в квадрате в соответствии с уравнением
![]()
где cya – коэффициент подъемной силы;
ρ — плотность воздуха, кг/м3;
V – скорость воздушного потока, м/с;
S – площадь крыла, м2.
Если при падении горизонтальной скорости еще и штурвал подать от себя, уменьшая угол атаки, то самолет будет быстрее падать и большая вертикальная скорость при посадке может разрушить шасси или другие конструктивные части самолета. Поэтому после отскока самолета при грубой посадке нельзя отдавать ручку от себя при не критическом угле атаке. Ручку следует оставить в прежнем положении, не двигая от себя. Самолет сам опустится вниз из-за низкой горизонтальной скорости и сядет мягче из-за меньшей вертикальной скорости.
Если отскок при слишком грубой посадке самолета оказался большим и самолет взлетел метров на 10, то есть смысл перевести двигатели на взлетный режим, отдавая ручки газа от себя, и уйти на второй круг.
Не соблюдение этих положений при грубой посадке SSJ-100 5 мая 2019 года в Шереметьево могло быть одной из ошибок пилотов и привести к значительной вертикальной скорости перед вторым касанием самолета, разрушению топливных баков и катастрофе.
Виртуально-общественное КБ летательных аппаратов "Кукушка" http://www.vokb-la.spb.ru/
Авиационные документы ИКАО, правила, сертификаты типа http://www.aviadocs.net/
bА – средняя аэродинамическая хорда (САХ), м;
bСГХ - средняя геометрическая хорда (СГХ), м;
![]() -
относительная координата центра масс (Ц.М.);
-
относительная координата центра масс (Ц.М.);
xТ – расстояние центра масс самолета от носка (САХ), м;
χ - угол стреловидности крыла по 1/4 хорд, градусы;
bго - средняя хорда горизонтального оперения, м;
![]() -
относительная толщина горизонтального оперения;
-
относительная толщина горизонтального оперения;
ℓго - размах горизонтального оперения, м;
Sго – площадь горизонтального оперения, м2;
λго – удлинение горизонтального оперения, м;
Lго – плечо горизонтального оперения (расстояние от ц. м. до 0,25 bго), м;
bво - средняя хорда вертикального оперения, м;
![]() -
относительная толщина вертикального оперения;
-
относительная толщина вертикального оперения;
ℓво - размах вертикального оперения, м;
Sво – площадь вертикального оперения, м2;
λво – удлинение вертикального оперения, м;
Lво – плечо вертикального оперения (расстояние от ц. м. до 0,25 bво), м;
nр – расчетный коэффициент перегрузки;
αзакл – угол заклинения крыла – угол между хордой крыла и осью фюзеляжа, градусы;
H – высота шасси, м;
λ – угол выноса шасси, градусы;
φ - стояночный угол, градусы;
φ1 – угол опрокидывания (угол между плоскостью ВПП и касательной к основным и предохранительной опорам), градусы.
1.Ефимов В.В. Основы авиации. Часть I. Основы аэродинамики и динамики полета летательных аппаратов: Учебное пособие. – М.: МГТУ ГА, 2003. – 64 с.
2.Демонова Т.В., Медведев В.П. Основы аэродинамики и гидромеханики: учеб. пособие. Таганрог: ТАВИАК, 2011. 283 с.
Сайт: super-code.ru
©