© 2018 Ольшевский Андрей Георгиевич консультирует по авиации, двигателям, искусственному интеллекту, генерации идей, электронике, физике, математике, информатике, программированию, техническим дисциплинам в Скайп da.irk.ru

Сайт www.super-code.ru наполняется бесплатными книгами. Книги периодически редактируются

Электродинамика и распространение радиоволн

1 Общие положения и математический аппарат электродинамики

1.1 Электромагнитное поле

Электромагнитное поле состоит из электрического поля, взаимозависимого с магнитным полем. Электрическое поле представляют вектор электрической индукции , функционально зависимый от вектора напряженности электрического поля . Магнитное поле представляют вектор магнитной индукции , функционально зависимый от напряженности магнитного поля .

Векторы электромагнитного поля в общем случае представляют нестационарное электромагнитное векторное поле, являющееся функцией координат и времени:

- напряженность электрического поля;

- напряженность магнитного поля;

- электрическая индукция;

- магнитная индукция.

Стационарное электромагнитное векторное поле, является функцией координат и не зависит от времени:

- напряженность электрического поля;

- напряженность магнитного поля;

- электрическая индукция;

- магнитная индукция.

Скорость распространения электромагнитных волн в вакууме равна скорости света

c = 3·10⁸ м/с.

где λ - длина волны, м;

T - период, с.

Частота, Гц

c = λf

Круговая частота, с^-1

ω = 2πf.

Чем больше длина электромагнитной волны, тем меньше частота. Электромагнитные волны начинаются с меньшей частоты, затем начинаются радиоволны диапазонов сверхдлинных, длинных волн, далее средние волны с большей частотой, короткие, ультракороткие волны с еще большей частотой. За радиоволнами следует инфракрасное излучение с меньшей длиной волны, но большей частотой, чем у радиоволн. Видимый свет, начинается с волн красного цвета. Названия цветов начинаются с букв в порядке поговорки: "Каждый охотник желает знать, где сидит фазан". Заканчивается видимый свет волнами фиолетового цвета. Далее следуют: ультрафиолетовое, рентгеновское, гамма излучения и космическая радиация.

Теория электромагнитного поля базируется на векторном исчислении и векторных полях, наиболее важные положения которых рассмотрим ниже.

1.2 Скалярные и векторные поля

1.2.1 Потенциальное (безвихревое) и вихревое векторные поля

Линии потенциального (безвихревого) поля начинаются в истоке и заканчиваются в стоке. Линии вихревого (соленоидального) поля не имеют источников, всегда замкнуты, непрерывны (см. рисунок [4]).

Рисунок — Потенциальное (безвихревое) и вихревое поля

Циркуляция вектора потенциального поля по замкнутому контуру L равна нулю

Поток вектора вихревого поля через замкнутую поверхность S равен нулю

Электростатическое поле может быть только потенциальным (безвихревым), магнитное поле является только вихревым.

1.2.2 Градиент скалярного поля, оператор Гамильтона

Градиент (перепад) скалярного поля φ - это вектор, показывающий в каком направлении наиболее быстро увеличивается φ, равный по величине производной по этому направлению

Условный вектор или оператор Гамильтона

Градиент скалярного поля φ, записанный с помощью оператора Гамильтона (оператора «набла»)

Поверхность уровня φ содержит одинаковые значения φ = const скалярного поля, поэтому градиент скалярного поля φ перпендикулярен поверхности уровня φ и направлен в сторону увеличения φ (см. рисунок [4]).

Рисунок — Градиент скалярного поля

1.2.3 Дивергенция (расходимость)

Дано векторное поле в точке (x; y; z)

где - единичные векторы (орты) в направлениях осей координат x, y, z соответственно.

Для векторного поля в точке (x; y; z) дивергенция (расходимость) в точке P равна пределу потока вектора через поверхность S, ограничивающую объем V, деленного на V при стремлении V к нулю

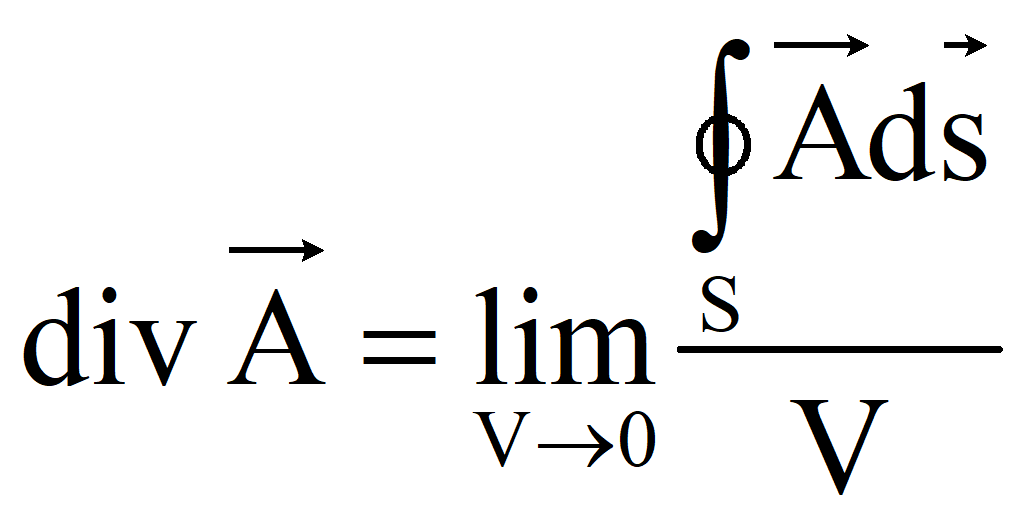
Значения дивергенции в точках P векторных полей (см. рисунок [4]).

Рисунок — Значения дивергенции

При расходимости большей нуля

внутри области V находятся источники векторного поля .

При отрицательной расходимости

внутри области V находятся стоки векторного поля .

При расходимости равной нулю

силовые линии поля пронизывают область V или замкнуты (вихревое поле).

1.2.4 Ротор (вихрь)

Ротор (вихрь) позволяет оценить степень вращения в какой-то точке (x; y; z) векторного поля

где - единичные векторы (орты) в направлениях осей координат x, y, z соответственно.

Для векторного поля в точке (x; y; z) проекция ротора на направление нормали к поверхности, равна пределу циркуляции вектора вокруг контура C, деленной на площадь ΔS поверхности, ограниченной контуром C, при стремлении ΔS к нулю

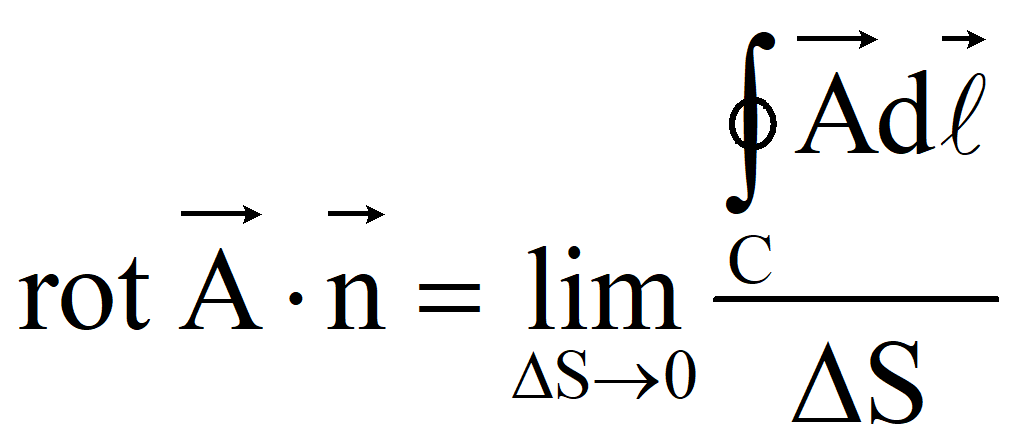
Направление нормали связано с направлением обхода контура C правилом правого винта.

Ротор (вихрь) векторного поля , используя оператор Гамильтона

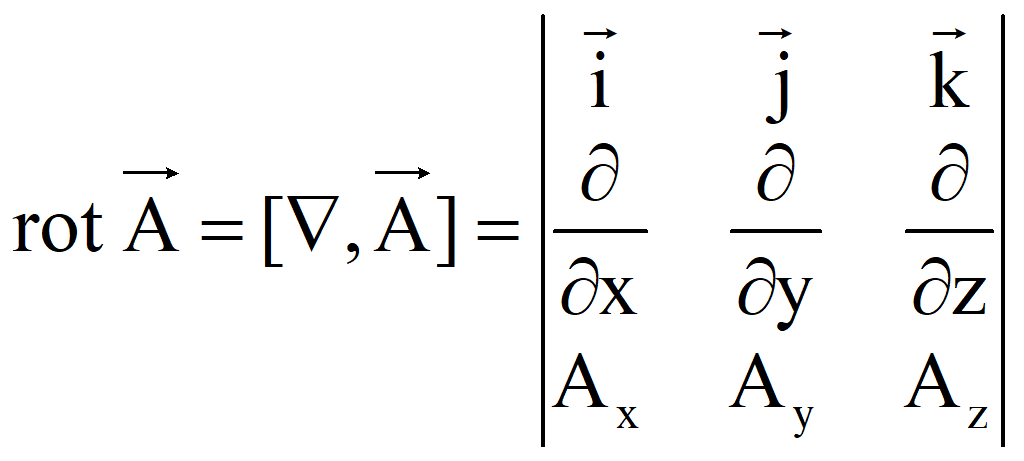
Проекции вектора на оси координат

Если в точке P ротор равен нулю

,

то вращения в этой точке нет и векторное поле потенциальное.

1.3 Виды распределения зарядов

Объемная плотность зарядов, Кл/м³

Заряд, сосредоточенный в объеме V, Кл

Поверхностная плотность зарядов, Кл/м²

Заряд, сосредоточенный на поверхности S, Кл

Линейная плотность зарядов, Кл/м

Заряд нити, Кл

Заряд точечных зарядов равен сумме N зарядов конечной величины

1.4 Электрическое поле

Вектор электрического смещения (электрической индукции) равен электрической постоянной ε₀, умноженной на скобку, в которой единица складывается с электрической восприимчивостью χ_э, умноженной на вектор напряженности электрического поля

Электрическая постоянная

Вектор электрического смещения (электрической индукции) в веществе

где ε - абсолютная электрическая проницаемость.

Вектор электрической индукции в вакууме

.

1.5 Магнитное поле

Вектор магнитной индукции равен магнитной постоянной μ₀, умноженной на скобку, в которой единица складывается с магнитной восприимчивостью χ_м, умноженной на вектор напряженности магнитного поля

Магнитной постоянная

Вектор магнитной индукции в веществе

где μ - абсолютная магнитная проницаемость.

Вектор магнитной индукции в вакууме

1.6 Закон Ома в дифференциальной форме

Закон Ома для участка цепи

U = IR

Плотность тока

Выразим

Проинтегрируем по и получим зависимость тока от плотности тока

Закон Ома в дифференциальной форме позволяет определить плотность тока, А/м²

где σ - удельная проводимость среды, См/м.

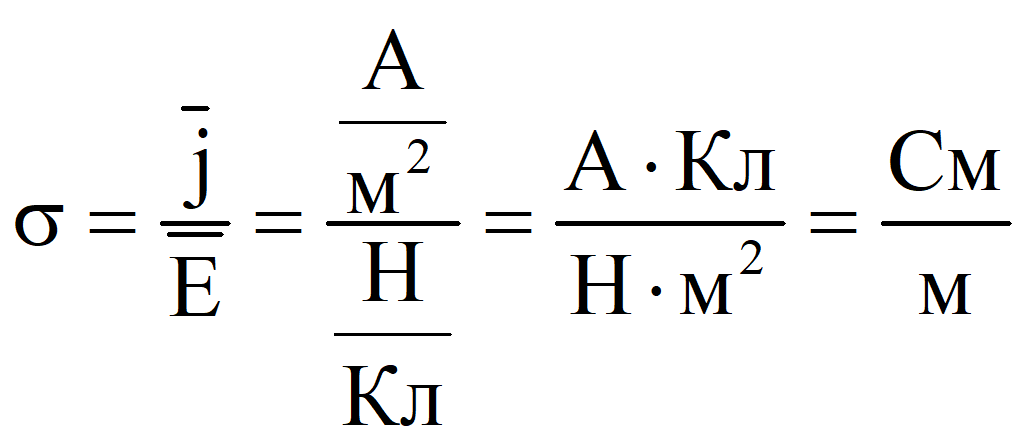
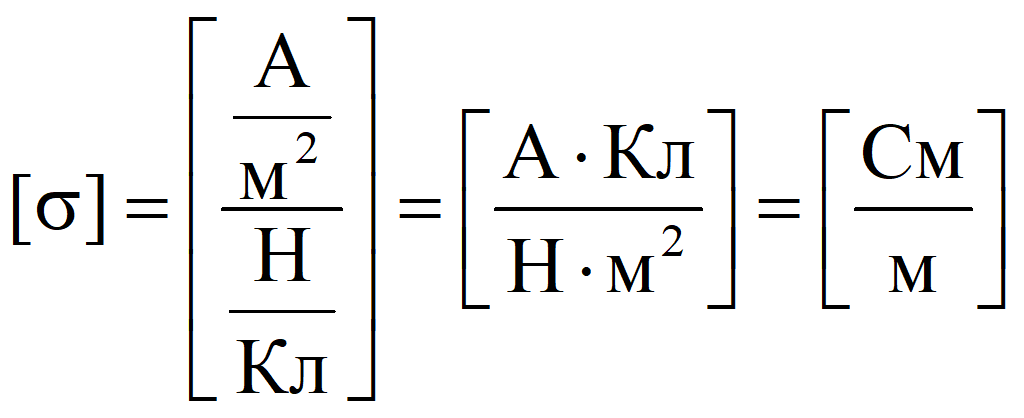
2 Уравнения Максвелла

Система уравнений Максвелла в дифференциальной форме описывает переменные электромагнитные поля

Векторы в уравнениях Максвелла представляют нестационарное электромагнитное векторное поле, являющееся функцией координат x, y, z и времени t.

2.1 Частные случаи электромагнитных явлений

В частных случаях уравнения Максвелла могут упрощаться.

2.1.1 Стационарное электромагнитное поле

Стационарное электромагнитное поле создается постоянными токами и описывается векторными функциями координат, не зависящими от времени:

- напряженность электрического поля;

- электрическая индукция;

- напряженность магнитного поля;

- магнитная индукция.

Векторные функции не зависят от времени, поэтому частные производные по времени в уравнениях Максвелла равны нулю:

Система уравнений Максвелла в дифференциальной форме принимает вид, описывающий стационарное электромагнитное поле:

2.1.2 Статические электрические или магнитные поля

Статические поля не изменяются со временем и не имеют движущихся зарядов, следовательно, токов

.

Система уравнений Максвелла разделяется на две независимые друг от друга системы уравнений. Первая система характеризует электростатическое поле и называется системой дифференциальных уравнений электростатики

Вторая система уравнений описывает магнитостатическое поле, создаваемого постоянными неподвижными магнитами

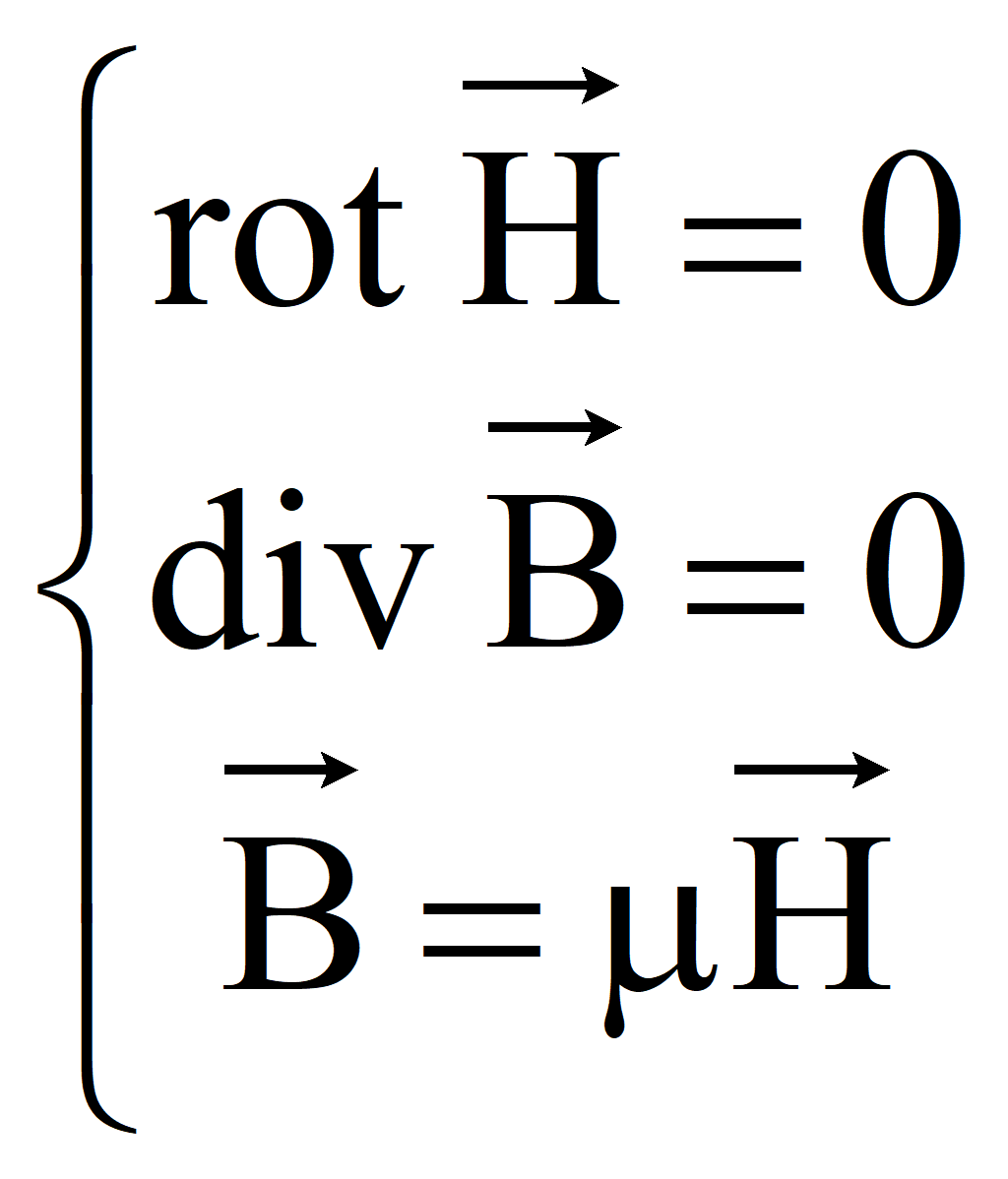
Эта система уравнений может использоваться для описания магнитных полей, созданных постоянными токами, но в областях, в которых плотность тока равна нулю , и которые не сцеплены с током (не охватывают линии тока).

2.1.3 Уравнения Максвелла в комплексной форме

Если векторы электромагнитного поля изменяются во времени по гармоническим законам, то система уравнений Максвелла может быть представлена в комплексной форме, не содержащей времени, для комплексных векторов

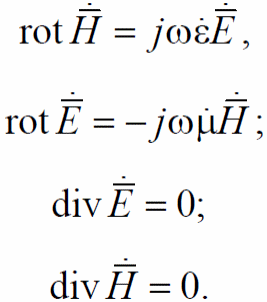
или комплексных амплитуд

2.1.4 Волновые уравнения

Из уравнений Максвелла в комплексной форме, выражая отдельно уравнения для комплексных векторов и получаются волновые уравнения Гельмгольца для векторов

и комплексных амплитуд

где - волновое число, для вакуума

.

3 Плоские электромагнитные волны

На больших расстояниях от источника элемент сферической волны приближенно можно принять плоским. Плоские волны не могут быть созданы источниками, они придуманы для значительного упрощения теории электромагнитных волн в отдельных случаях.

Векторы напряженности электрического и магнитного полей плоской волны синфазные и осциллируют вдоль взаимно перпендикулярных направлений в плоскости, перпендикулярной направлению распространения волны. Такие волны являются поперечными [3] (см. рисунок).

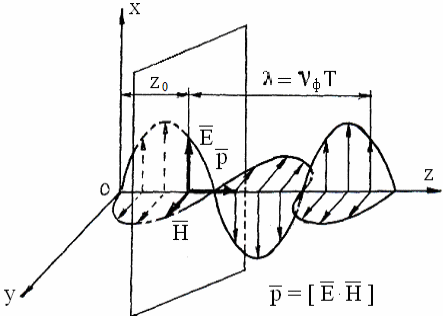
Рисунок - Мгновенная картина распределения напряженности электрического и магнитного полей вдоль направления распространения плоской волны. Во времени картина поля перемещается в пространстве с фазовой скоростью v_ф вдоль оси z

Фронт волны представляет собой геометрическое место точек поля с одинаковой фазой: у плоской волны (см. рисунок) одной из этих поверхностей является плоскость z = z₀, перпендикулярная направлению распространения волны [3]. Параметры поля при перемещении в пределах фронта волны не изменяются.

Фронт плоской волны является плоскостью, перпендикулярной направлению распространения волны. Параметры поля при перемещении в пределах этой плоскости не изменяются, поэтому частные производные по направлениям x и y равны нулю:

Волновые уравнения Гельмгольца для плоской волны становятся одномерными для векторов

и комплексных амплитуд

Решение дифференциальных уравнений для векторов

где , - орты в направлении векторов электрической и магнитной напряженностей соответственно;

A, B, C, D – коэффициенты.

Действительные части векторов

Проанализируем в первом уравнении первое слагаемое. На рисунке [1; стр. 113] покажем положение максимума электрического поля в моменты времени t (точка A) и t + Δt.

Рисунок — Положение максимумов электрического поля

За время Δt положение максимума переместилось на Δz, можем записать равенство

Acos(ωt − kz) = Acos(ωt + ωΔt − kz − kΔz),

в котором аргументы равны

ωt − kz = ωt + ωΔt − kz − kΔz

0 = ωΔt - kΔz

ωΔt = kΔz.

Отсюда получаем фазовую скорость v_ф — скорость распространения фронта волны

Для вакуума

,

поэтому фазовая скорость в вакууме

Подставим значения констант

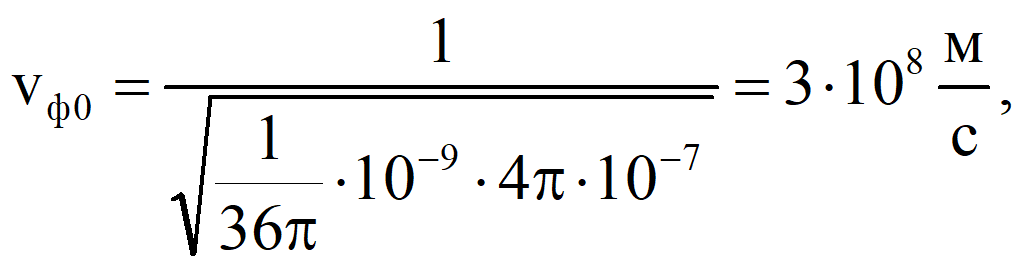
следовательно, в вакууме скорость распространения фронта волны равна скорости света.

Фазовая скорость в какой-то среде

Фазовая скорость не зависит от частоты.

Амплитуды двух точек на расстоянии длины волны λ с фазами, отличающимися на 2π равны, поэтому выполняется равенство

cos(ωt − kz) = cos(ωt − k(z + λ) + 2π),

в котором аргументы равны

ωt − kz = ωt − k(z + λ) + 2π,

ωt − kz = ωt − kz − kλ + 2π.

Сократим ωt − kz

0 = − kλ + 2π,

kλ = 2π.

Отсюда длина волны

Для произвольной среды

,

поэтому длина волны

В вакууме длина волны

Длина волны в остальных средах

Волновое сопротивление вакуума

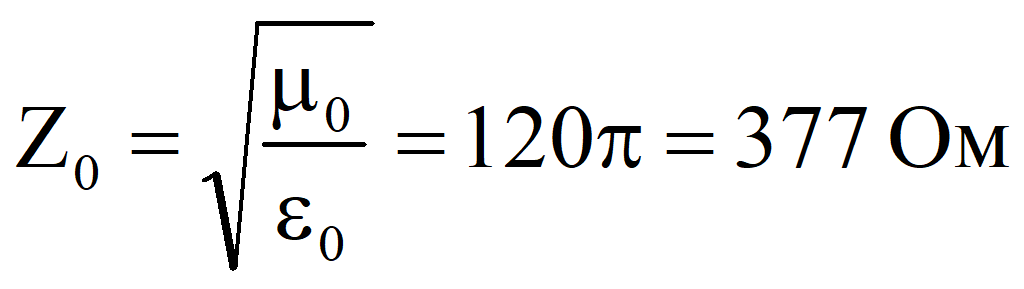
Для сухого воздуха принимается такое же волновое сопротивление.

4 Распространение радиоволн

Все электромагнитные волны, в том числе и радиоволны распространяются в вакууме со скоростью 3·10⁸ м/с.

4.1 Распространение радиоволн в свободном пространстве

Распространение радиоволн в атмосфере, вдоль земной поверхности, в земной коре, в космическом пространстве нашей галактики и за ее пределами примем за свободное распространение радиоволн, которое и рассмотрим.

4.1.1 Классификация радиоволн по диапазонам

Радиоволны имеют диапазон частот от тысяч герц до тысяч гигагерц: 3·10³ — 3·10¹² Гц. У длинных волн частота меньше, чем у коротких волн, имеющих большую частоту.

Применение радиоволн возможно благодаря передающему устройству, природной среде распространения радиоволн и приемному устройству, все вместе образующими радиолинию.

Земные атмосфера и поверхность являются средами поглощающими, электрически неоднородными, имеющими не постоянную во времени и пространстве проводимость, диэлектрическую проницаемость, зависящие от частоты распространяющихся радиоволн.

Поэтому радиоволны были разделены на диапазоны частот с примерно одинаковыми условиями распространения радиоволн в пределах этих диапазонов частот. Диапазоны частот приняты Международным консультативным комитетом по радио (МККР) в соответствии с Регламентом радиосвязи.

Для радиосвязи используются и волны оптического диапазона: инфракрасные, видимые и ультрафиолетовые.

Мощность электромагнитных волн зависит от частоты в 4-й степени

P ~ ω⁴.

Волны с большей частотой, но с меньшей длиной волны способны обладать большей мощностью.

Антенны с узкой диаграммой направленности имеют размеры значительно превышающие длину волны, для высоких частот проще сделать такие высокоэффективные антенны.

Чем выше несущая частота, тем большее число независимых модулируемых каналов может передаваться такими радиоволнами.

4.2 Положения из теории антенн

Пространство вокруг антенны разделяется на три области, имеющих различную структуру полей и расчетных формул: ближняя, промежуточная и дальняя. В реальных линиях связи обычно имеет место дальняя область (зона Фраунгофера) на расстояниях от антенны

где L – максимальный размер излучающей области антенны, м;

λ – длина волны, м.

Характеристическое (волновое) сопротивление свободной среды

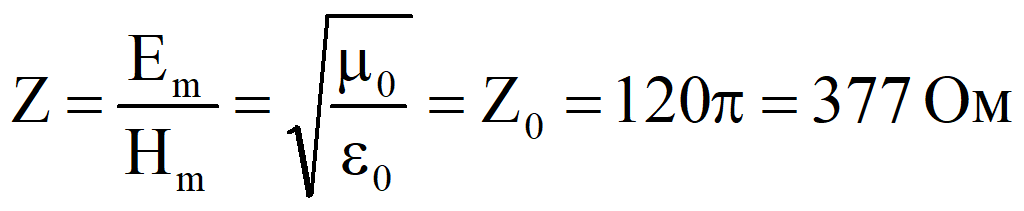
Вектор Пойнтинга (вектор Умова - Пойнтинга), Вт/м²

где P – мощность, Вт;

r – расстояние от антенны до точки наблюдения, м.

где D – коэффициент направленного действия (КНД) антенны.

Среднее значение вектора Пойнтинга в дальней зоне

Из соотношения

выразим амплитуду напряженности магнитного поля

Подставим

Приравняем векторы Пойнтинга

Сократим

Амплитуда напряженности электрического поля в дальней зоне антенны в свободном пространстве

Напряженность поля в других направлениях определяется с помощью диаграммы направленности антенны F(θ,α), в которой углы θ и α в сферической системе координат (r,θ,α) задают направление на точку наблюдения:

5 Распространение радиоволн различных диапазонов

5.1 Распространение сверхдлинных и длинных волн

Сверхдлинные волны (СДВ) имеют длину волны более 10 000 м и частоту менее 30 кГц. Длинные волны (ДВ) имеют длину волны от 1000 до 10 000 м и частоту 300-30 кГц.

СДВ и ДВ имеют большую длину волны, поэтому хорошо огибают земную поверхность. Токи проводимости этих радиоволн значительно превышают токи смещения для всех видов земной поверхности, поэтому происходит незначительное поглощение энергии при распространении поверхностной волны. Поэтому СДВ и ДВ могут распространяться на расстояния до 3 тыс. км.

СДВ и ДВ слабо поглощаются в ионосфере. Чем ниже частота радиоволны, тем требуется более низкая электронная концентрация ионосферы для поворота радиоволны к Земле. Поэтому, поворот СДВ и ДВ происходит в нижней границе ионосферы (днем в слое D и ночью в слое E) на высоте 80-100 км. Тропосфера на распространение СДВ и ДВ практически не влияет. Вокруг Земли СДВ и ДВ распространяются, отражаясь от ионосферы и от земной поверхности в сферическом слое 80-100 км между нижней границей ионосферы и земной поверхностью.

Линии связи на СДВ и ДВ обладают большой устойчивостью напряженности электрического поля. В течении суток и года величина сигнала мало меняется, а также не подвергается случайным изменениям. Поэтому СДВ и ДВ широко используются в навигационных системах.

Ограниченный частотный диапазон (3-300 кГц) СДВ и ДВ не позволяет разместить даже один телевизионный канал, для которого требуется полоса 8МГц.

Большая длина волны СДВ и ДВ диктует использование громоздких антенн.

Несмотря на недостатки, СДВ и ДВ используются в радионавигации, радиовещании, радиотелефонной и телеграфной связи в том числе и с подводными объектами, так как эти и оптические волны слабо поглощаются в морской воде.

5.2 Распространение средних волн

Средние волны (СВ) имеют длину волны от 100 до 1 000 м, частоту от 300 кГц до 3 МГц (0,3 - 3 МГц). Могут распространяться земные и ионосферные СВ, которые используются преимущественно в радиовещании.

Земные СВ-радиолинии ограничены протяженностью не более 1000 км из-за существенного поглощения СВ земной поверхностью.

Ионосферная СВ способна отразиться от слоя E ионосферы. Через самый низкий слой D ионосферы, появляющийся только днем, СВ проходят и сильно поглощаются в нем, практически исключая связь днем. Поэтому ночью в ионосфере поглощение СВ значительно уменьшается и на расстояниях больших 1000 км от передатчика связь восстанавливается.

Из-за интерференции ионосферных волн между собой или (и ночью) с земными волнами возникают случайные замирания сигнала (фединг). Антифединговые антенны имеют прижатый к земной поверхности максимум диаграммы направленности для борьбы с замираниями и перекрестной модуляцией на СВ.

5.3 Распространение коротких волн

Короткие волны (КВ) имеют длину волны от 10 до 100 м (в 10 раз короче средних волн), частоту от 3 до 30 МГц (в 10 раз больше частоты СВ). КВ используются преимущественно для радиовещания.

КВ сильно поглощаются земной поверхностью и плохо огибают поверхность Земли, поэтому земные КВ распространяются лишь на несколько десятков километров.

КВ испытывают поглощение и проходят в самых нижних слоях ионосферы D и E, но отражаются от слоя F.

Расчет КВ линий связи заключается в составлении графика рабочих частот в зависимости от времени суток (волнового расписания).

5.4 Особенности распространения ультракоротких волн

Ультракороткие волны (УКВ) имеют длину волны менее 10 м и частоту более 30 МГц. По частоте снизу УКВ граничат с КВ, а сверху с инфракрасными волнами. Ионосфера для УКВ прозрачна, поэтому УКВ-линии применяются в основном в пределах прямой видимости.

УКВ имеют большой частотный диапазон, способный передавать значительные объемы информации. На метровых и дециметровых волнах можно разместить 297 телевизионных каналов. Во всем коротковолновом диапазоне разместятся всего 3 телевизионных канала, а во всем СВ диапазоне ни одного.

Развитие мобильной и спутниковой связи, Интернета и другие вышеуказанные причины заставляют радиотехнику переходить на более высокие частоты, поэтому УКВ приобретают все большую значимость.

5.4.1 Распространение ультракоротких волн в пределах прямой видимости

УКВ линии связи, работающие в пределах прямой видимости:

- УКВ и телевизионное вещание;

- радиолокационные станции (РЛС);

- радиорелейные линии связи (РРЛ);

- связь с космическими объектами;

- мобильная связь.

5.4.2 Распространение УКВ за горизонт

Дальнее распространение УКВ за линию горизонта происходит следующими способами:

- благодаря рассеянию на неоднородностях тропосферы;

- сверхрефракция в тропосфере;

- рассеивание на неоднородностях ионосферы;

- благодаря отражению от слоев ионосферы F₂ и E_S;

- благодаря отражению от метеорных следов;

- благодаря усилению препятствием (см. рисунок [1; стр. 387])

Рисунок — Распространение радиоволн при усилении препятствием

Перечень условных обозначений, символов, единиц и терминов

D,B – векторы электрической и магнитной индукции

Е,Н – векторы напряженностей электрического и магнитного поля

I(r, t) – электрический ток

j (r,t) − вектор плотности электрического тока

P −мощность электромагнитного поля

M – вектор намагниченности

P – вектор электрической поляризации

q – электрический заряд

ε,μ − абсолютные диэлектрическая и магнитная проницаемости

ε₀ ,μ₀ − диэлектрическая и магнитная постоянные

ε_r ,μ_r −относительные диэлектрическая и магнитная проницаемости

П – вектор Пойнтинга (вектор Умова - Пойнтинга)

ρ,ξ,τ – плотности объемного, поверхностного и линейного заряда

σ − удельная проводимость среды

ϕ – скалярный электростатический потенциал

χ_э ,χ_м – электрическая и магнитная восприимчивости

W − энергия электромагнитного поля

W_э ,W_м – энергии электрического и магнитного поля

w −плотность энергии электромагнитного поля

w_э ,w_м – плотности энергий электрического и магнитного поля

k – волновое число

СДВ – сверхдлинные волны

ДВ – длинные волны

СВ – средние волны

КВ – короткие волны

УКВ – ультракороткие волны

РЛС – радиолокационная станция

РРЛ – радиорелейная линия

D – коэффициент направленного действия (КНД) антенны

G – коэффициент усиления антенны

F(θ,α) – диаграмма направленности антенны

R₀ – радиус Земли (6371 км)

Z₀ − волновое сопротивление свободного пространства

Список использованных источников

1.Электродинамика и распространение радиоволн : учеб. пособие / Л.А. Боков, В.А. Замотринский, А.Е. Мандель. – Томск : Томск. гос. ун-т систем упр. и радиоэлектроники, 2013. – 410 с.

2.Морозов А.В. Электродинамика и распространение радиоволн : учебник для высш. военных учеб. заведений / Морозов А. В., Нырцов А. Н., Шмаков Н. П. - М. : Радиотехника, 2007. - 408 с.

3.Яманов Д.Н. Основы электродинамики и распространение радиоволн. Часть I. Основы электродинамики: Тексты лекций. - М.: МГТУ ГА, 2002. – 80 с.

4.Панько В.С. Лекции по курсу «Электродинамика и распространение радиоволн».

Сайт: super-code.ru

© 11.01.18 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru