© 2021 Ольшевский Андрей Георгиевич консультирует по математике, информатике, физике, авиации, двигателям, искусственному интеллекту, генерации идей, электронике, программированию, техническим дисциплинам в Скайп da.irk.ru

Сайт super-code.ru наполняется полезной информацией, которую можно скачать бесплатно

Алгебра 7, 8, 9, 10, 11 класс, определения и формулы

Оглавление

7 класс

Координатная плоскость

Прямоугольная система координат - это пересекающиеся взаимно перпендикулярные координатные прямые с началом отсчета в точке их пересечения, превращающая плоскость в координатную плоскость.

Линейное уравнение с двумя переменными

Линейное уравнение с двумя переменными

ax + by + c = 0,

где a, b, c - коэффициенты (числа);

x, y - переменные.

Решением уравнения с двумя переменными, например ax + by + c = 0, называют пару чисел (x; y), удовлетворяющих этому уравнению, то есть дающих верное числовое равенство при подстановке решения в заданное уравнение.

Задача. Найти два решения уравнения 2x + 5y + 7 = 0 и построить график функции

Решение

Выразим y через x

5y = -2x - 7

y = -0,4x - 1,4

При x = 0

y = -0,4·0 - 1,4

y = -1,4

Первое решение (0; -1,4).

При x = -3

y = -0,4·(-3) - 1,4

y = 1,2 - 1,4

y = -0,2

Второе решение (-3; -0,2).

Алгоритм нахождения решения линейного уравнения с двумя переменными ax+by+c=0

1.Выразить переменную y через переменную x

by = - ax - c

2.Задать конкретное значение переменной x = x₁; найти значение y = y₁

Получили решение (x₁; y₁).

Алгоритм построения графика линейного уравнения с двумя переменными ax+by+c=0

1.Выразить переменную y через переменную x

by = - ax - c

2.Задать конкретное значение переменной x = x₁; найти значение y = y₁

Получили решение (x₁; y₁).

3.Задать другое конкретное значение переменной x = x₂; найти значение y = y₂

Получили решение (x₂; y₂).

4.Построить точки (x₁; y₁) и (x₂; y₂) на координатной плоскости xOy.

5.Через эти две точки провести прямую, которая и является графиком линейного уравнения ax + by + c = 0.

Задача. Построить график функции 20x + 10y - 5 = 0.

Решение

Выразить переменную y через переменную x

10y = -20x + 5

y = -2x + 0,5

Задача. Построить график функции -40x - 8y + 32 = 0.

Задача. Построить график функции ax + by + c = 0 при a = 1, b = 1 и c = 1

Решение

x + y + 1 = 0

Выразим y через x

y = - x - 1

Это уравнение линейной функции, поэтому для построения графика функции достаточно двух точек

При x = -1

y = - (-1) - 1 = 1 - 1 = 0.

При x = 5

y = - 5 - 1 = -6.

Формулы сокращенного умножения

Квадрат суммы (a + b)² = a² + 2ab + b².

Квадрат разности (a - b)² = a² - 2ab + b².

Разность квадратов a² - b² = (a - b)(a + b).

Разность кубов a³ - b³ = (a - b)(a² + ab + b²).

Сумма кубов a³ + b³ = (a + b)(a² – ab + b²).

Куб разности (a - b)³ = a³ - 3a²b + 3ab² - b³.

Куб суммы (a + b)³ = a³ + 3a²b + 3ab² + b³.

8 класс

9 класс

Числовая функция

Функция y = f(x) – это правило f, которое устанавливает зависимость между конкретным значением независимой переменной x (аргументом) и зависимой от нее переменной y, имеющей единственное значение.

Область определения функции

Область определения функции D(f) или X – это множество значений независимой переменной x, при которых функция y = f(x) существует.

Задание функции y = f(x) на области определения X или D(f)

Задать функцию y = f(x) на области определения X или D(f) – значит каждому аргументу x из множества X или D(f) поставить в соответствие единственное значение y. Задание функции записывается одним из способов:

y = f(x), x ϵ X;

y = f(x), x ϵ D(f)

Область значений функции

Область значений функции E(f) – это множество всех значений функции y = f(x) при x ϵ X.

Способы задания функции

Основные способы задания фунций:

1.Аналитический – функция y = f(x) задается формулой (формулами).

2.Графический - графиком функции y = f(x).

3.Табличный - таблицей со переменной x и соответствующими им значениями y.

4.Словесный.

Четные и нечетные функции

Для четной функции f(x), x ϵ X выполняется равенство

f(-x) = f(x),

для нечетной функции f(x), x ϵ X выполняется равенство

f(-x) = -f(x)

для любого x из множества X.

Область определения D(f) четной или нечетной функции y = f(x) является симметричным множеством.

Если область определения D(f) не является симметричным множеством или условия четности и нечетности функции f(x) не выполняются, то функция ни четная, ни нечетная.

Законы сложения

1.Переместительный закон a + b = b + a.

2.Распределительный закон (a + b) + c = a + (b + c).

Законы умножения

Для любых рациональных чисел a, b и c справедливы законы умножения

1.Переместительный закон ab = ba.

2.Сочетательный закон (ab)c = a(bc).

3.Распределительный закон (a + b)c = ac + bc.

Числовая последовательность

Числовой последовательностью называют функцию y = f(x) натурального аргумента x ϵ N, которую обозначают y = f(n) или y₁, y₂, …, y_n, где индекс n ϵ N.

График числовой последовательности представляет из себя набор точек с натуральным аргументом и значениями функции, вычисленными в этих точках.

Аналитический способ задания числовой последовательности

Последовательность задается аналитически формулой n-го члена y_n = f(n).

Словесный способ задания последовательности

При словесном способе правило составления последовательности описывается словами, а не формулой.

Рекуррентный способ задания последовательности

При рекуррентном (от латинского слова recurrere – возвращаться) способе n-ный член последовательности вычисляется по правилу или формуле на основе предыдущих членов последовательности. Обычно задаются 1-2 первых члена последовательности.

Например, последовательность y₁ = 2; y_n = y_n-1 + 3, при n > 1 задана рекуррентно.

Арифметическая прогрессия

Арифметической прогрессией называется числовая последовательность, каждый последующий член, которой, начиная со второго, отличается от предыдущего на величину разности арифметической последовательности d.

Арифметическая прогрессия задается рекуррентно:

a₁,

a_n = a_n-1 + d, n > 1

где первый член a₁ и разность арифметической прогрессии d – заданны числами;

a_n – член прогрессии, начиная со второго;

a_n-1 – предыдущий член арифметической прогрессии.

d - разность между последующим и предыдущим членами прогрессии:

d = a_n – a_n-1 = a_n+1 – a_n = a₂ - a₁.

n – ный член арифметической прогрессии

a_n = a₁ + (n – 1)d

Сумма n членов арифметической прогрессии:

Подставим a_n = a₁ + (n – 1)d

Задача 16.31 [Алгебра. 9 класс. В 2 ч. Ч.2. Задачник Мордкович А.Г. и др. 2010 - 223с].

Дано:

a₂ + a₅ = 18; a₂a₃ = 21; a₃ > 0.

Решение

a₃ > 0 ⇒ a₂ > 0 ⇒ a₅ > 0

a_n = a₁ + d(n - 1)

a₂ = a₁ + d

a₃ = a₁ + 2d

a₅ = a₁ + 4d

Подставляем в заданную систему

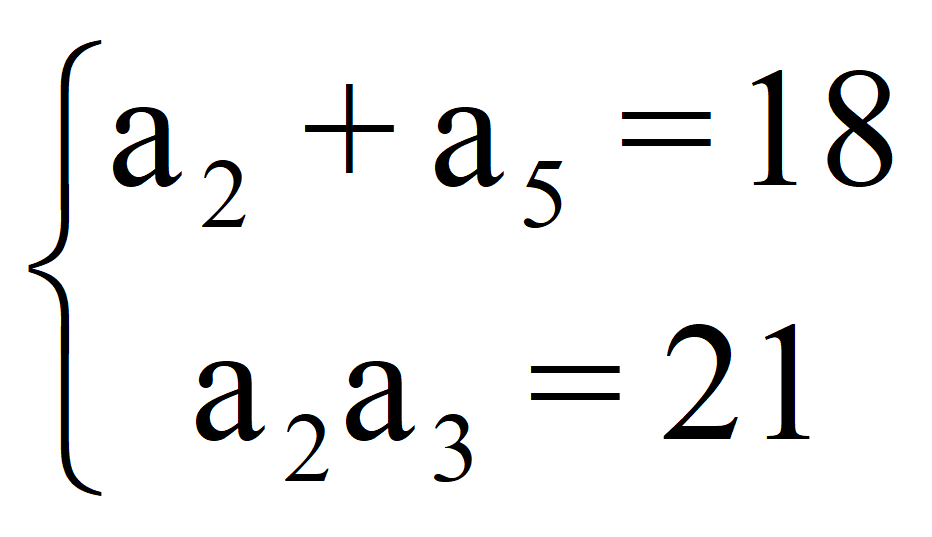
и получаем систему уравнений

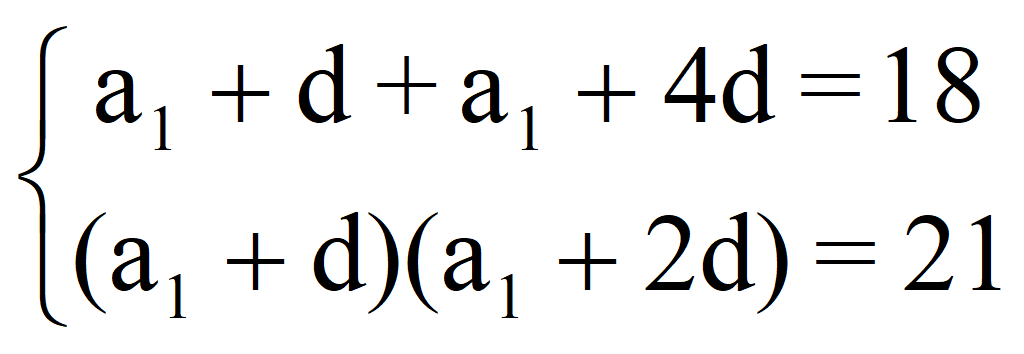
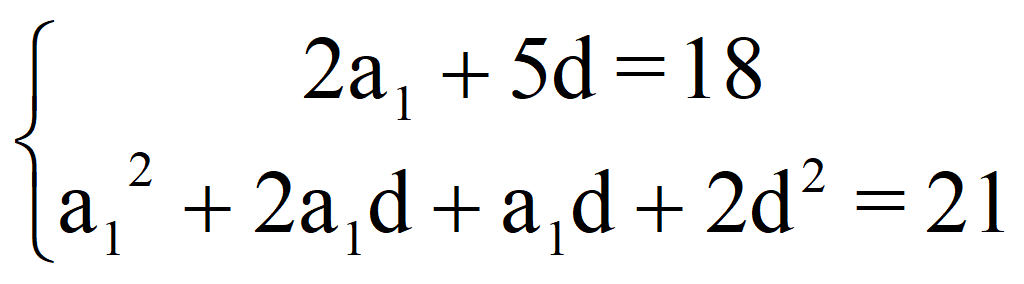
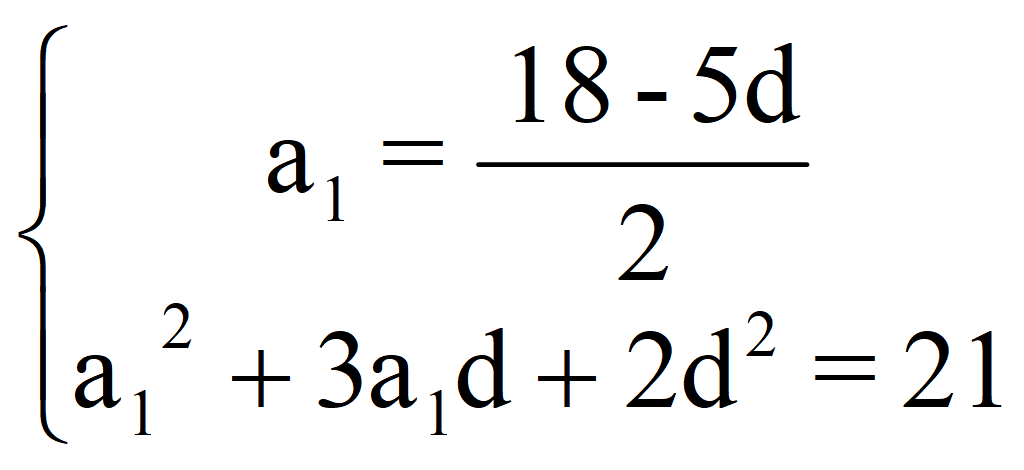
81 – 45d + 6,25d² + 27d – 7,5d² + 2d² = 21;

0,75d² – 18d + 81 – 21 = 0;

0,75d² – 18d + 60 = 0.

Разделим на 0,75, то есть умножим на 4/3

d² – 24d + 80 = 0.

По теореме Виета

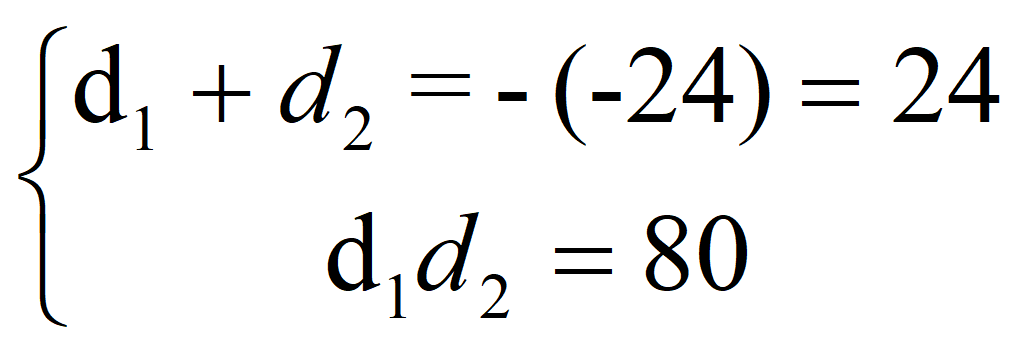
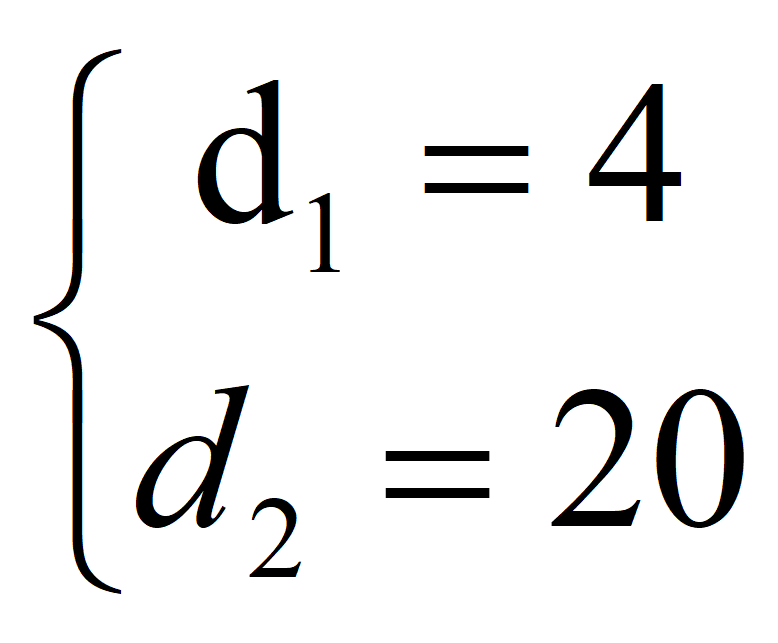
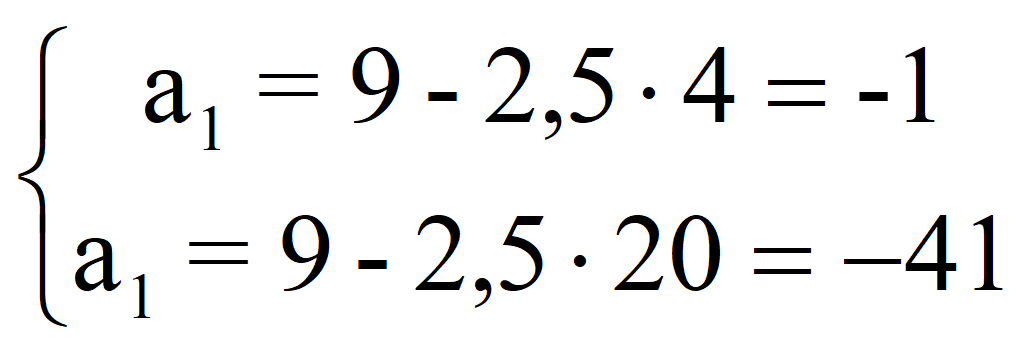
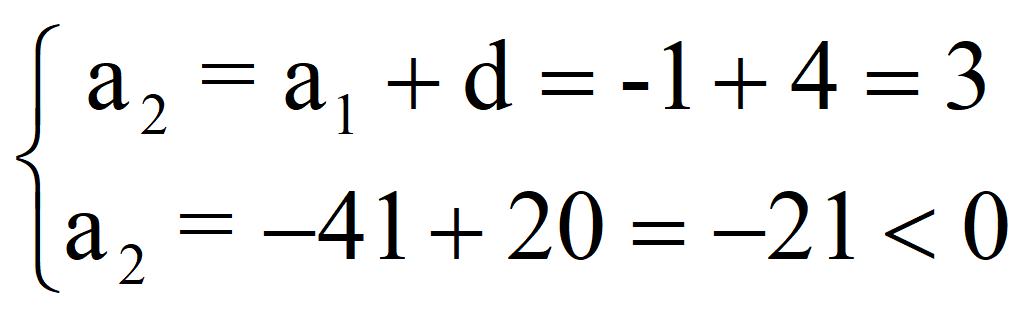
Следовательно, a₁ = -1; d = 4; a₂ = 3;

a₃ = a₂ + d = 3 + 4 = 7;

a₄ = a₃ + d = 7 + 4 = 11;

a₅ = a₄ + d = 11 + 4 = 15.

Проверка

a₂ + a₅ = 3 + 15 = 18

a₂a₃ = 3·7 = 21.

Ответ: a₁ = -1; a₂ = 3; a₃ = 7; a₄ = 11; a₅ = 15.

Геометрическая прогрессия

Геометрической прогрессией называется ненулевая числовая последовательность, каждый последующий член, которой, начиная со второго, получается из предыдущего умножением на знаменатель геометрической прогрессии q.

Геометрическая прогрессия задается рекуррентно:

b₁,

b_n = b_n-1·q, n > 1

где первый член b₁ и знаменатель геометрической прогрессии q – заданны числами;

b_n – член прогрессии, начиная со второго;

b_n-1 – предыдущий член арифметической прогрессии.

Знаменатель геометрической прогрессии

n-ный член геометрической прогрессии

b_n = b_1·q^n-1,

Сумма n-членов геометрической прогрессии

Задача 17.12 (б) [Мордкович. Задачник 9 класс]

Найдите b₁ и q для геометрической прогрессии (b_n), заданной следующими условиями:

b₄ = 1,

Решение

Знаменатель геометрической прогрессии

Формула 4-го члена геометрической прогрессии:

b₄ = b₁q^4-1 = b₁q³.

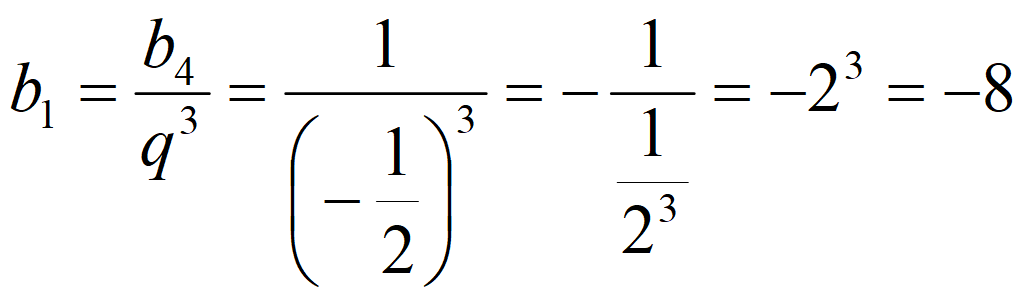
Задача 17.22 (б) [Мордкович. Задачник 9 класс]

Найдите b₁ и q для геометрической прогрессии (b_n), заданной следующими условиями:

b₂ = 24, b₅ = 81.

Решение

Знаменатель геометрической прогрессии

Формула 2-го члена геометрической прогрессии:

b₂ = b₁q^2-1 = b₁q.

Формула 5-го члена геометрической прогрессии:

b₅ = b₁q^5-1 = b₁q⁴.

Получаем систему уравнений

;

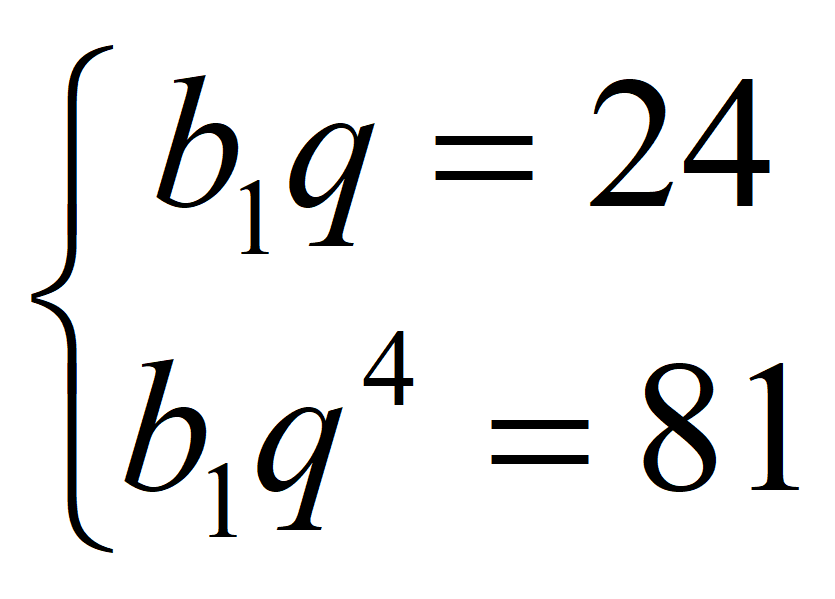
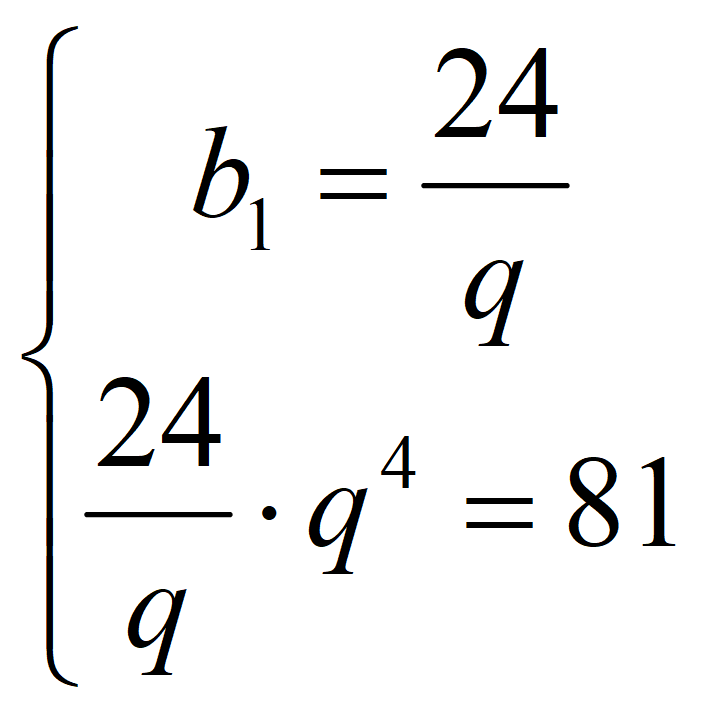
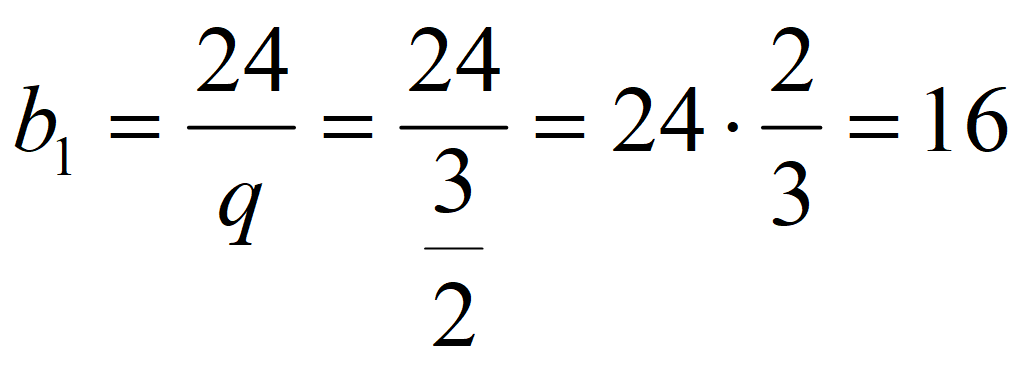
17.26 (а)

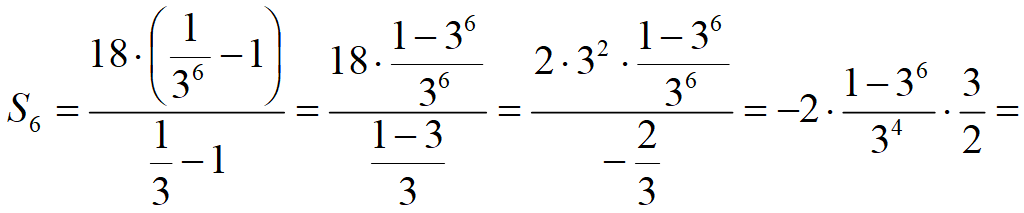
= 26,(962).

= 26,(962).

10 класс

Признак делимости на 11

Признак делимости на 7 или 13

Натуральное число делится на 7 или 13, если алгебраическая сумма чисел

Простые и составные числа

Простым называется число, имеющее только два делителя - само число и 1.

Составным называется число, имеющее больше двух делителей.

Число 1 не является ни простым, ни составным, так как делится лишь на 1.

Произвольное натуральное число, большее 1 имеет как минимум один простой делитель.

Множество простых чисел бесконечно [10].

Расстояние между двумя соседними простыми числами может быть больше любого наперед заданного натурального числа [10].

График функции y = f(x+a)+b, полученный из графика функции y=f(x)

График функции y = f(x + a) + b, получается из графика функции y = f(x) путем перемещения на вектор (-a; b).

Обратные тригонометрические функции

Нечетными являются функции y = arcsinx и y = arctgx. Функции y = arcosx и y = arcctgx не являются ни четными, ни нечетными.

Тригонометрические формулы

Сложение и вычитание аргументов

Формулы двойного угла

sin2α = 2sinαcosα

cos2α = cos²α – sin²α = 1 - 2sin²α = 2cos²α – 1

Формулы понижения степени

Сложение и вычитание функций

Преобразование произведения в сумму и разность

Если α + β = 90⁰, то

Методы решения тригонометрических уравнений

Приравнять к нулю и разбить на множители

Подстановка

Универсальная тригонометрическая подстановка

При x ≠ π + 2πn

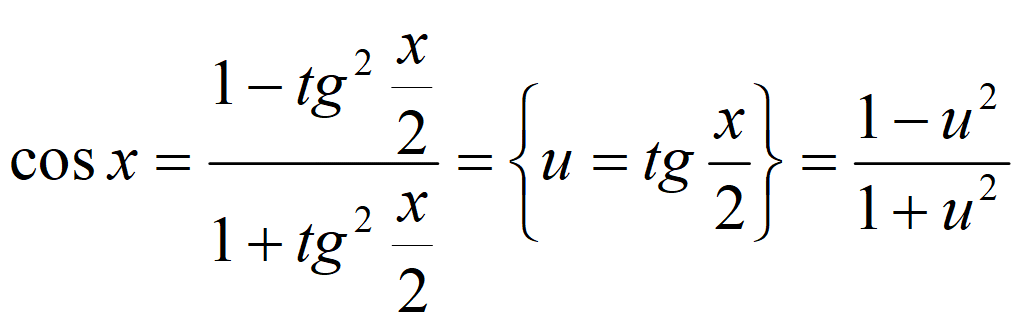
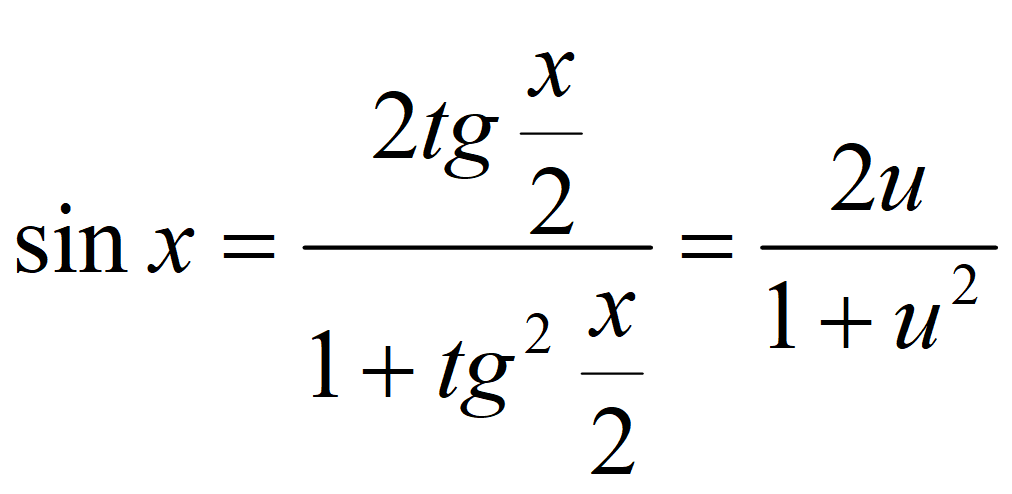
11 класс

Многочлены от одной переменной

Стандартным видом многочлена p(x) является расположение его одночленов по убыванию степеней его одночленов

p(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₃x³ + a₂x² + a₁x + a₀,

где a_nxⁿ - старший член многочлена;

a_n - коэффициент при старшем члене, если a_n ≠ 1, то многочлен называется неприведенным, но если имеется возможность поделить многочлен на a_n, то коэффициент при старшем члене становится равным 1 и многочлен называется приведенным;

a₀ - свободный член.

Два многочлена равны, когда они имеют одинаковые коэффициенты при одинаковых степенях переменной.

Если многочлен p(x) делится на многочлен q(x), то в результате получается многочлен s(x).

Если многочлен p(x) не делится на многочлен q(x), то в результате получается многочлен s(x) плюс остаток r(x), степень которого меньше степени многочлена q(x).

При делении многочлена ненулевой степени p(x) на двучлен x - a

Опубликовано 18.05.21

© 2021 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru