© 2021 Ольшевский Андрей Георгиевич репетитор по математике, физике, информатике, программированию по Скайп da.irk.ru
Сайт супер код ру super-code.ru с полезными темами, которые можно сохранить бесплатно
Векторы на плоскости и в пространстве, способы решения задач, примеры, формулы
Оглавление
2 Вектор на плоскости и в пространстве 5
5 Лемма о коллинеарных векторах 13
6 Произведение вектора на число 13
Репетитор по математике, информатике, физике, программированию, техническим дисциплинам
8 Разложение вектора по двум неколлинеарным векторам 16
10 Разложение вектора по трем некомпланарным векторам 18
11 Прямоугольная система координат в пространстве 18
12 Координаты вектора в пространстве 19
13 Координаты вектора, радиус-вектора и точки 20
14 Длина вектора и расстояние между двумя точками 21
15 Координаты середины отрезка 23
17 Проекция вектора на прямую 24
18 Скалярное произведение векторов 25
19 Физический смысл скалярного произведения векторов 26
20 Скалярное произведение векторов в координатах 28
21 Условие перпендикулярности векторов 28
Векторы на плоскости и в пространстве (продолжение)
Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru
Векторы на плоскости и в пространстве веб-страницы: 1 2 3
1 Введение
Векторы на плоскости и в пространстве, векторные поля используются не только в математике, но и в физике, например, в электродинамике. Векторы позволяют эффектно решать геометрические задачи второй части ЕГЭ и аналитической геометрии в пространстве.
Векторы в пространстве включают геометрия 10, 11 класса, аналитическая геометрия. Векторы в пространстве даются аналогично векторам на плоскости, но учитывается третья координата z. Исключение из векторов в пространстве третьего измерения дает векторы на плоскости, которые изучаются в геометрии 8, 9 класса.
2 Вектор на плоскости и в пространстве
Вектором называется направленный отрезок с началом и концом, изображаемым на рисунке стрелкой. Произвольная точка пространства может считаться нулевым вектором. Нулевой вектор не имеет конкретного направления, так как начало и конец совпадают, поэтому ему можно придать любое направление.
Длина
(модуль) ненулевого вектора
- это длина отрезка AB, которая
обозначается
.
Длина вектора
обозначается
.
Нулевой вектор имеет длину равную нулю
= 0.
Коллинеарными
называются ненулевые векторы, лежащие на одной прямой или на
параллельных прямых. На рисунках ниже изображены коллинеарные векторы
,
.
На
рисунке ниже также изображены коллинеарные векторы
,
и
.
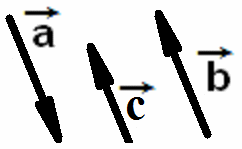
Нулевой вектор коллинеарен любому вектору.
Сонаправленными
называются коллинеарные ненулевые векторы, имеющие одно направление.
Сонаправленные векторы обозначаются знаком ↑↑. Например,
если вектор
сонаправлен с вектором
,
то используется запись
↑↑
.
На рисунках ниже изображены сонаправленные векторы.
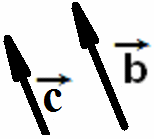
Нулевой вектор сонаправлен с любым вектором.
Равными
называются сонаправленные векторы равной длины. На рисунке ниже
изображены равные векторы
=
.
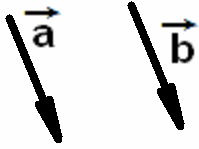
Противоположно
направленными называются два коллинеарных ненулевых вектора, имеющих
противоположное направление. Противоположно направленные векторы
обозначаются знаком ↑↓. Например, если вектор
противоположно направлен вектору
,
то используется запись
↑↓
.
На рисунках ниже изображены противоположно направленные векторы.
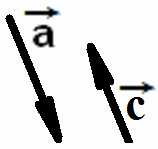
Противоположными
называются два ненулевых противоположно направленных вектора равной
длины. Вектор -
является противоположным вектору
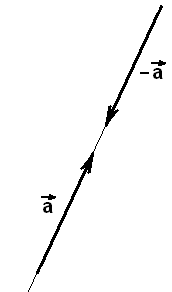
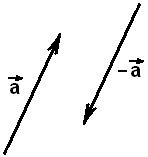
Противоположные векторы противоположно направленные и равны по модулю. Если даны точки A и B, то следующие векторы противоположные
Равные по модулю равные или противоположные, или нулевые векторы.
Многие физические величины являются векторными величинами: сила, скорость, электрическое поле и т.д.
Если не задана точка приложения (начала) вектора, то она выбирается произвольно.
Если в точку O поместить начало вектора, то считается, что вектор отложен от точки O. Из любой точки можно отложить единственный вектор, равный данному вектору.
3 Сумма векторов
Для сложения двух векторов по правилу треугольника проводится вектор 1, из конца этого вектора 1 проводится вектор 2, суммой данных вектора 1 и вектора 2 является вектор 3, проведенный из начала вектора 1 к концу вектора 2:
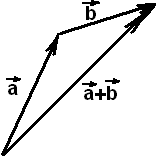
Для произвольных точек A, B и C можно написать сумму векторов:
+
=
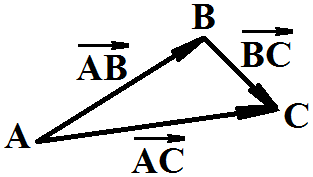
Если два вектора выходят из одной точки
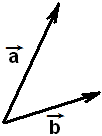
то их лучше складывать по правилу параллелограмма.
Для сложения двух векторов по правилу параллелограмма, складываемые векторы 1 и 2 откладываются из одной точки, из концов этих векторов 1 и 2 достраивается параллелограмм путем прикладывания к концу одного вектора начала другого. Вектор 3, образованный диагональю параллелограмма, берущий начало от точки начала складываемых векторов, будет являться суммой векторов 1 и 2 (см. рисунок ниже).
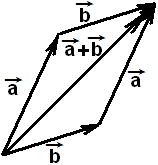
Правило
параллелограмма содержит в себе два разных порядка сложения векторов
по правилу треугольника. Можно к концу вектора
приложить начало вектора
или к концу вектора
приложить начало вектора
.
Результаты сложения в этих случаях и будут определяться по правилу
треугольника.
Законы сложения векторов:
1.
Переместительный закон
+
=
+
.
2.
Сочетательный закон (
+
)
+
=
+ (
+
).
Если необходимо сложить несколько векторов, то векторы складываются попарно или по правилу многоугольника: из конца вектора 1 проводится вектор 2, из конца вектора 2 проводится вектор 3, из конца вектора 3 проводится вектор 4, из конца вектора 4 проводится вектор 5 и т. д. Вектор, являющийся суммой нескольких векторов, проводится от начала вектора 1 до конца последнего складываемого вектора.
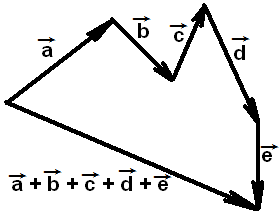
По законам сложения векторов порядок сложения векторов не влияет на результирующий вектор, являющийся суммой нескольких векторов.
4 Разность векторов
Разность векторов можно записать в виде суммы векторов
-
=
+ (-
),
где
"-
"
- вектор, противоположный вектору
.
Векторы
и -
можно складывать по правилу треугольника или параллелограмма.
Пусть
даны векторы
и
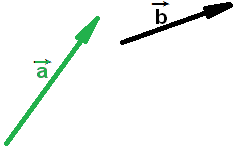
Для
нахождения разности векторов
-
строим вектор -
,
противоположный вектору
.
Векторы
и -
складываем по правилу треугольника, прикладывая к концу вектора
начало вектора -
,
и получаем вектор
+
(-
)
=
-
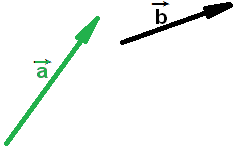
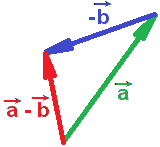
Отложим
начала векторов
и -
из одной точки
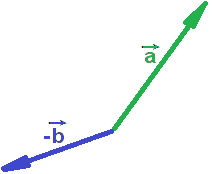
Векторы
и -
складываем по правилу параллелограмма
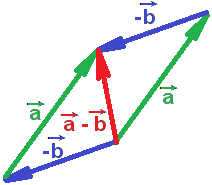
на диагонали получили вектор
+
(-
)
=
-
Если
векторы
и
берут начало из одной точки
,
то
разность векторов
-
дает вектор, соединяющий их концы и стрелка на конце результирующего
вектора ставится в направлении того вектора, от которого отнимают
второй вектор
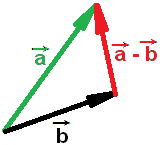
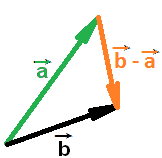
Рисунок ниже демонстрирует сложение и разность векторов
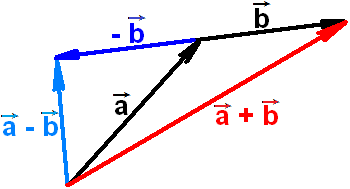
Рисунок ниже демонстрирует сложение и разность векторов разными способами (знаки векторов над буквами не показаны)
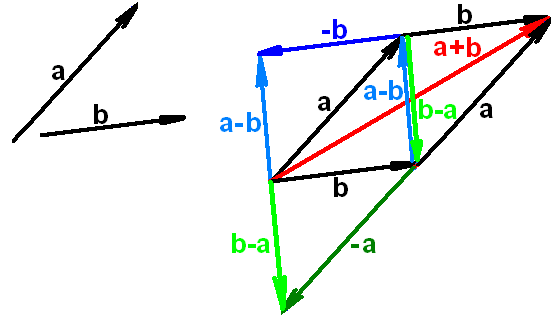
Задача.
Даны векторы
и
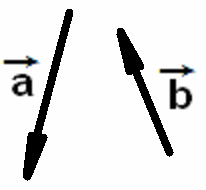
Изобразить сумму и разность векторов всеми возможными способами во всевозможных сочетаниях векторов.
5 Лемма о коллинеарных векторах
Если
векторы
и
коллинеарны, то приравнять их можно с помощью коэффициента k
=
k
6 Произведение вектора на число
Произведение
ненулевого вектора
на число k дает вектор
=
k
,
коллинеарный
вектору
.
Например,
вектор
= 2
дает вектор
сонаправленный вектору
и в 2 раза длиннее вектора
.
Например,
вектор
= -4
дает вектор
противоположно направленный вектору
и в 4 раза длиннее вектора
.
Длина
вектора
:
|
|
= |k|·|
|.
Для соотношения векторов
=
k
проанализируем все возможные варианты в зависимости от коэффициента k:
-
если k > 0, то
векторы
и
сонаправленные.
-
если k = 0, то
вектор
нулевой.
-
если k < 0, то
векторы
и
противоположно направленные.
-
если |k| = 1, то
векторы
и
равной длины.
-
если k = 1, то
и
равные векторы.
-
если k = -1, то
и
противоположные векторы.
-
если |k| > 1,
то длина вектора
больше длины вектора
.
-
если k > 1, то
векторы
и
сонаправленные и длина
больше длины вектора
.
-
если k < -1,
то векторы
и
противоположно направленные и длина
больше длины вектора
.
-
если |k| < 1,
то длина вектора
меньше длины вектора
.
-
если 0 < k <
1, то векторы
и
сонаправленные и длина
меньше длины вектора
.
-
если -1 < k <
0, то векторы
и
противоположно направленные и длина
меньше длины вектора
.
Произведение нулевого вектора на любое число дает нулевой вектор.
Задача.
Дан вектор
Построить
векторы 2
,
-3
,
0,5
,
-1,5
.
Задача.
Даны векторы
и
.
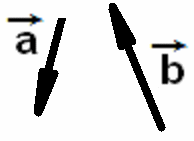
Построить
векторы 3
+
2
.
Решение
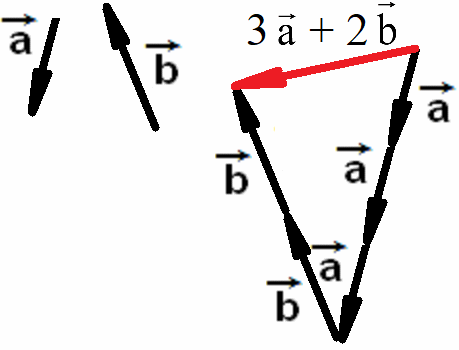
Векторы
2
- 2
,
-2
-
предлагается построить самостоятельно.
Законы, описывающие умножение вектора на число
1.
Сочетательный закон (kn)
=
k(n
)
2.
Первый распределительный закон k(
+
)
= k
+
k
.
3.
Второй распределительный закон (k + n)
= k
+
n
.
Для
коллинеарных векторов
и
,
если
≠ 0, существует единственное число k,
позволяющее выразить вектор
через
:
=
k
.
Это число равно
7 Компланарные векторы
Компланарными называются векторы, лежащие в одной плоскости или в параллельных плоскостях. Если провести векторы, равные данным компланарным векторам из одной точки, то они будут лежать в одной плоскости. Поэтому можно сказать, что компланарными называются векторы, если имеются равные им векторы, лежащие в одной плоскости.
Два произвольных вектора всегда компланарны потому что всегда можно подобрать две параллельные плоскости, в которых будут лежать эти векторы. Три вектора могут быть компланарными или не компланарными. Три вектора, из которых хотя бы два коллинеарные, всегда компланарны. Коллинеарные векторы всегда компланарны.
8 Разложение вектора по двум неколлинеарным векторам
Любой
вектор
единственным образом разлагается на плоскости по двум неколлинеарным
ненулевым векторам
и
с единственными коэффициентами разложения x
и y:
=
x
+ y
Любой
вектор
,
компланарный ненулевым неколлинеарным векторам
и
,
единственным образом разлагается по этим двум векторам
и
с единственными коэффициентами разложения x
и y:
=
x
+ y
Разложим
на плоскости заданный ненулевой вектор
по данным ненулевым неколлинеарным векторам
и
:
Если
векторы
,
и
компланарные, то на плоскости проведем их из одной точки, построив
векторы равные заданным компланарным векторам
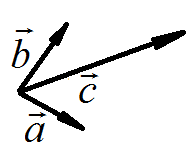
Из
конца вектора
проведем прямые, параллельные векторам
и
до пересечения с прямыми, проведенными через вектора
и
.
Получим параллелограмм
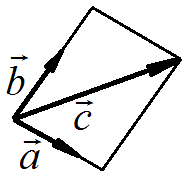
Длины
сторон параллелограмма получаются путем умножения длин векторов
и
на числа x и y,
которые определяются путем деления длин сторон параллелограмма на
модули (длины) соответствующих им векторов
и
.
Получаем разложение вектора
по заданным неколлинеарным векторам
и
:
=
x
+ y
В
решаемой задаче x ≈ 1,3, y
≈ 1,9, поэтому разложение вектора
по заданным неколлинеарным векторам
и
можно записать в виде
=
1,3
+ 1,9
.
Разложим
на плоскости заданный ненулевой вектор
по данным ненулевым неколлинеарным векторам
и
:
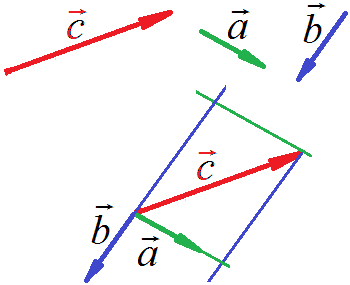
В
решаемой задаче x ≈ 1,3, y
≈ -1,9, поэтому разложение вектора
по заданным неколлинеарным векторам
и
можно записать в виде
=
1,3
- 1,9
.
9 Правило параллелепипеда
Параллелепипед - это объемная фигура, противоположные грани которой состоят из двух равных параллелограммов, лежащих в параллельных плоскостях.
Правило параллелепипеда позволяет складывать три некомпланарных вектора, которые откладываются из одной точки и строится параллелепипед так, чтобы суммируемые векторы образовывали его ребра, а остальные ребра параллелепипеда были соответственно параллельны и равны длинам ребер, образованных суммируемыми векторами. Диагональ параллелепипеда образует вектор, являющийся суммой заданных трех векторов, который начинается из точки начала складываемых векторов.
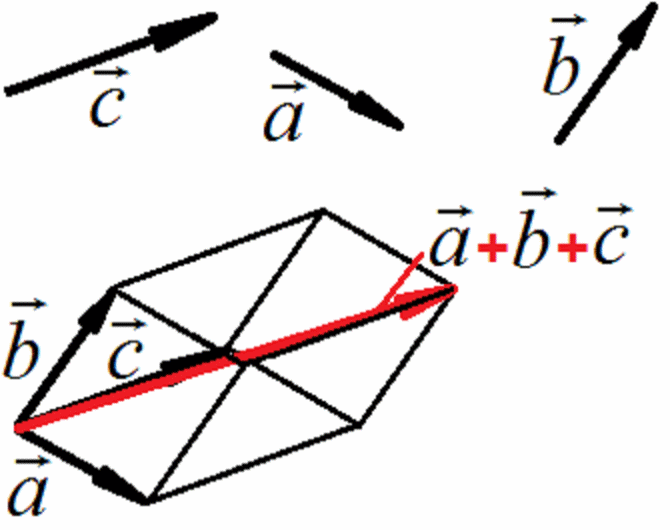
10 Разложение вектора по трем некомпланарным векторам
Любой
вектор
разлагается по трем заданным ненулевым некомпланарным неколлинеарным
векторам
,
и
с единственными коэффициентами разложения x,
y, z:
=
x
+ y
+
z
.
11 Прямоугольная система координат в пространстве
В трехмерном пространстве прямоугольная система координат Oxyz задается началом координат O и пересекающими в ней взаимно перпендикулярными координатными осями Ox, Oy и Oz с выбранными положительными направлениями, указанными стрелками, и единицей измерения отрезков. Если масштаб отрезков одинаковый по всем трем осям, то такая система называется декартовой системой координат.
Координата x называется абсциссой, y - ординатой, z - аппликатой. Координаты точки M в заданной системе координат записываются в скобках M (x; y; z).
12 Координаты вектора в пространстве
В
пространстве зададим прямоугольную систему координат Oxyz.
От начала координат в положительных направлениях осей Ox,
Oy, Oz проведем
соответствующие единичные векторы
,
,
,
которые называются координатными векторами, неколлинеарны и
некомпланарны. Поэтому любой вектор
,
проведенный из начала координат, разлагается по трем заданным
некомпланарным координатным векторам
,
и
с единственными коэффициентами разложения x,
y, z:
=
x
+ y
+
z
.
Коэффициенты
разложения x, y,
z являются координатами вектора
,
проведенного из начала заданной прямоугольной системы координат,
которые записываются в скобках
(x;
y; z). Координаты
конца такого вектора являются и координатами вектора. Нулевой вектор
имеет координаты равные нулю
(0;
0; 0). У равных векторов соответствующие координаты равны.
Если вектор начинается не из начала координат, то для определения его координат можно провести его из начала координат, совместив с точкой O начало вектора.
Правила нахождения координат результирующего вектора:
1.
При суммировании двух и более векторов каждая координата
результирующего вектора равна сумме соответствующих координат
заданных векторов. Если даны два вектора
(x1; y1;
z1) и
(x2; y2;
z2), то сумма векторов
+
дает вектор с координатами (x1 +
x2; y1
+ y2; z1
+ z2)
+
= (x1 + x2;
y1 + y2;
z1 + z2).
2.
Разность является разновидностью суммы, поэтому разность
соответствующих координат дает каждую координату вектора, полученного
при вычитании двух заданных векторов. Если даны два вектора
(xa;
ya;
za) и
(xb;
yb;
zb),
то разность векторов
-
дает вектор с координатами (xa
- xb;
ya -
yb; za
- zb)
-
= (xa
- xb;
ya -
yb; za
– zb).
3.
При умножении вектора на число каждая координата результирующего
вектора равна произведению этого числа на соответствующую координату
заданного вектора. Если даны число k и
вектор
(x;
y; z), то
умножение вектора на число k дает вектор k
с координатами
k
= (kx; ky; kz).
Задача.
Найти координаты вектора
= 2
- 3
+
4
,
если координаты векторов
(1; -2; -1),
(-2; 3; -4),
(-1; -3; 2).
Решение
=
2
+ (-3
)
+ 4
2
= (2·xa;
2·ya;
2·za)
= (2·1; 2·(-2); 2·(-1)) = (2; -4; -2);
-3
=
(-3·xb;
-3·yb;
-3·zb)
= (-3·(-2); -3·3; -3·(-4)) = (6; -9; 12);
4
=
(4·xc;
4·yc;
4·zc)
= (4·(-1); 4·(-3); 4·2) = (-4; -12; 8).
=
(2 + 6 - 4; -4 - 9 -12; -2 + 12 + 8) = (4; -25; 18).
13 Координаты вектора, радиус-вектора и точки
Координаты вектора - это координаты конца вектора, если начало вектора поместить в начало координат.
Радиус-вектор - это вектор, проведенный из начала координат к данной точке, координаты радиус-вектора и точки равны.
Если
вектор
задан точками M1(x1;
y1; z1)
и M2(x2;
y2; z2),
то каждая из его координат равна разности соответствующих координат
конца и начала вектора
=
(x2
- x1;
y2
- y1;
z2
- z1)
= (xa; ya; za)
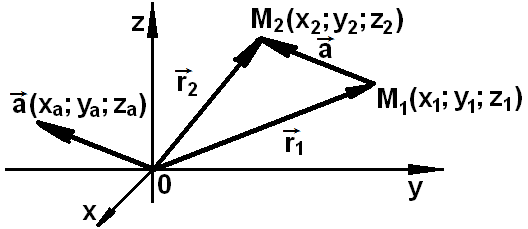
Для
коллинеарных векторов
=
(x1; y1;
z1) и
= (x2; y2;
z2), если
≠ 0, то существует единственное число k,
позволяющее выразить вектор
через
:
=
k
Тогда
координаты вектора
выражаются через координаты вектора
=
(kx1; ky1;
kz1) = (x2;
y2;
z2).
Отношение
соответствующих координат коллинеарных векторов
и
равно единственному числу k
Если
отношение соответствующих координат векторов
и
равно единственному числу k, то
эти векторы коллинеарны. В противном случае векторы
и
неколлинеарны.
14 Длина вектора и расстояние между двумя точками
Длина
вектора
(x; y; z)
равна корню квадратному из суммы квадратов его координат
Длина
(модуль) вектора
= (x2
- x1;
y2
- y1;
z2
- z1),
заданного точками начала M1 (x1;
y1; z1)
и конца M2 (x2;
y2; z2)
равна корню квадратному из суммы квадратов разности соответствующих
координат конца вектора и начала
Расстояние
d между двумя точками M1(x1;
y1; z1)
и M2(x2;
y2; z2)
равно длине вектора
Вынесем минусы за скобки, это приведет к смене знаков координат
Поменяем порядок координат
Вынесем -1 из под общей степени
-1 в квадрате равна 1
При определении длины вектора, заданного двумя точками, или расстояния между двумя точками не важен порядок вычитания соответствующих координат
На плоскости отсутствует координата z, поэтому на плоскости расстояние между точками M1(x1; y1) и M2(x2; y2)
Например, расстояние между точками A(-3; 4) и B(2; 1) на плоскости
15 Координаты середины отрезка
Если точка C - середина отрезка AB, то радиус-вектор точки C в произвольной системе координат с началом в точке O равен половине суммы радиус-векторов точек A и B
Если
координаты векторов
(x; y; z),
(x1; y1;
z1),
(x2; y2;
z2), то каждая координата
вектора
равна половине суммы соответствующих координат векторов
и
,
,
=
(x, y, z)
=
Каждая из координат середины отрезка равна полусумме соответствующих координат концов отрезка.
Можно вывести координаты любой точки на отрезке через координаты концов отрезка.
16 Угол между векторами
Угол
между векторами – равен углу между лучами, проведенными из
одной точки и сонаправленными с этими векторами. Обозначим угол между
векторами
и
буквой θ (тета) и два возможных варианта взаимного расположения
векторов изобразим на рисунках.
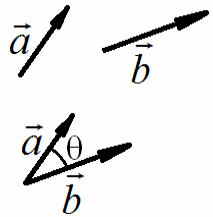
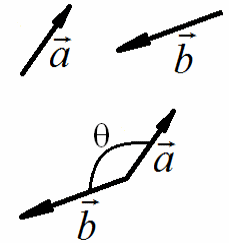
Угол между векторами может быть от 00 до 1800 включительно
00 ≤ θ ≤ 1800.
Угол между сонаправленными векторами равен 00. Если один вектор или оба нулевые, то угол между векторами, хотя бы один из которых нулевой, равен 00. Угол между перпендикулярными векторами равен 900. Угол между противоположно направленными векторами 1800.
17 Проекция вектора на прямую
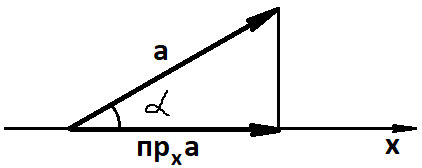
Проекция
вектора
на ось x
прxa = a·cosα.
18 Скалярное произведение векторов
Скалярное произведение двух векторов – это число (скаляр), равное произведению длин векторов на косинус угла между векторами
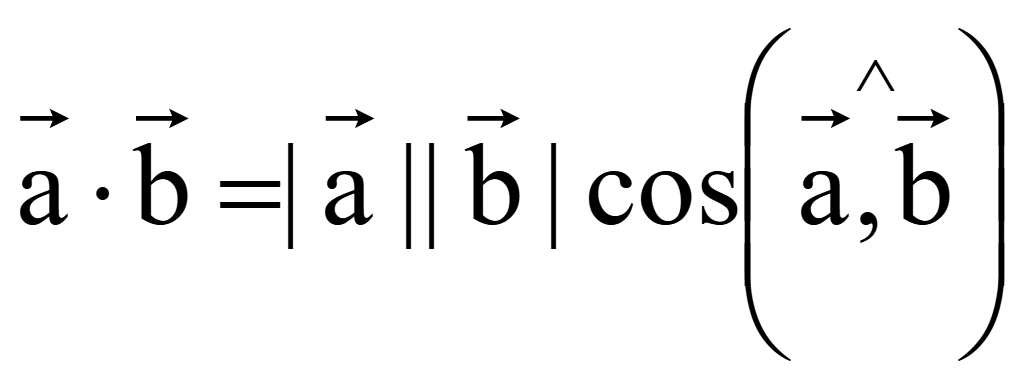
Если
=
00, то векторы сонаправлены
и
=
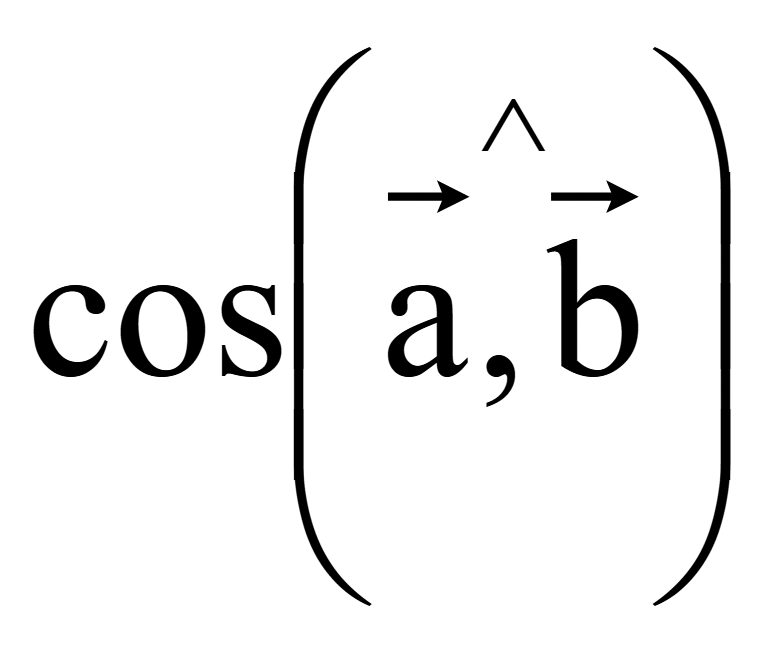cos 00 = 1,
следовательно, скалярное произведение сонаправленных векторов равно произведению их длин (модулей)
.
Если
угол между векторами 0 <
< 900, то косинус угла между такими векторами больше
нуля
,
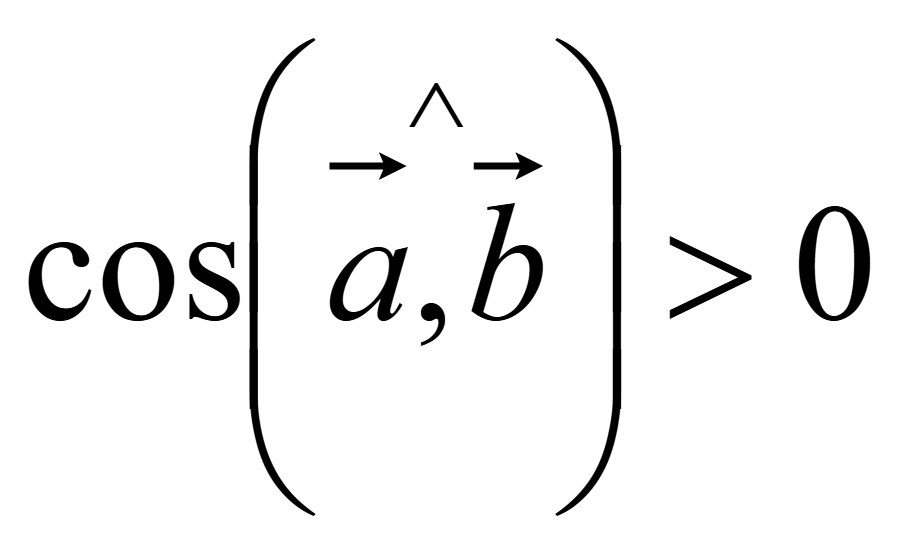следовательно скалярное произведение больше нуля
.
Если
ненулевые векторы перпендикулярны, то их скалярное произведение равно
нулю
,
так как cos900 = 0. Скалярное
произведение перпендикулярных векторов равно нулю.
Если
,
то косинус угла между такими векторами меньше нуля
,
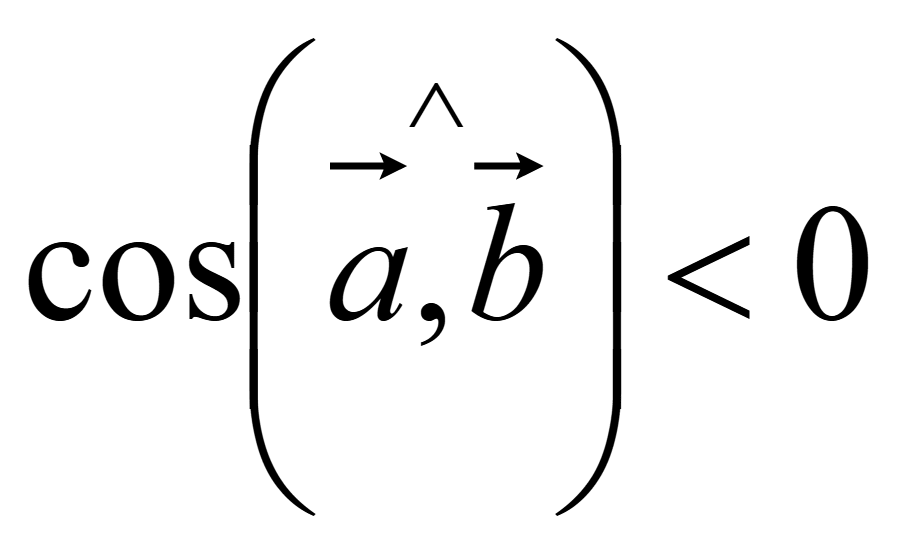следовательно скалярное произведение меньше нуля
.
При
увеличении угла между векторами косинус угла между ними
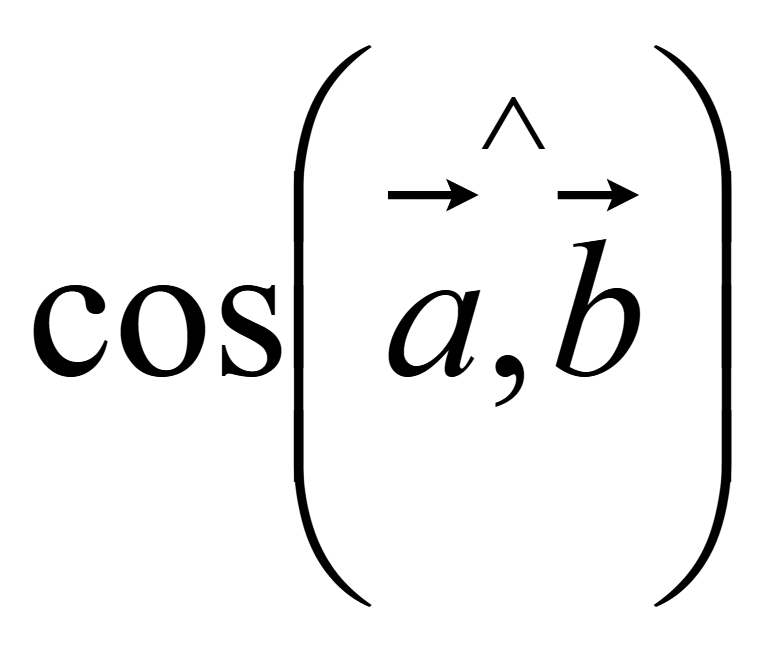уменьшается и достигает минимального значения при
=
1800, когда векторы противоположно направлены
.
Так как cos1800=-1, то
.
Скалярное произведение противоположно направленных векторов равно
отрицательному произведению их длин (модулей).
Скалярный квадрат вектора равен модулю вектора в квадрате
Скалярное произведение векторов, по крайней мере один из которых нулевой, равно нулю.
19 Физический смысл скалярного произведения векторов
Из
курса физики известно, что работа A силы
при перемещении тела
равна произведению длин векторов силы
и перемещения
на косинус угла между ними, то есть равна скалярному произведению
векторов силы и перемещения
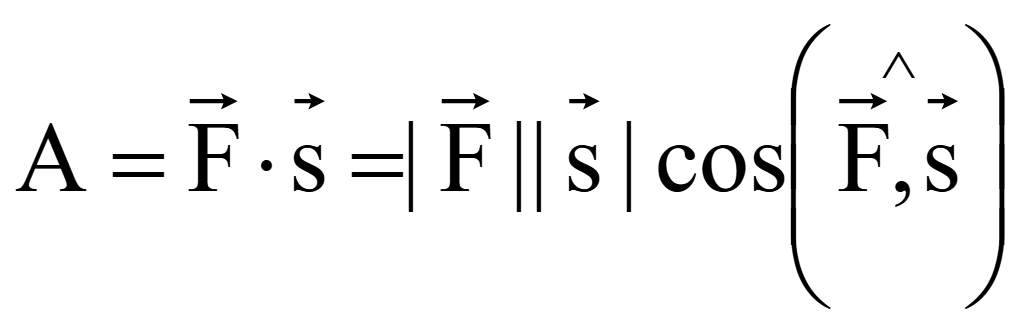
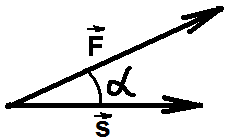
Если
вектор силы
сонаправлен с перемещением тела
,
то угол между векторами
=
00, следовательно работа силы
на перемещении
максимальна и равна A =
.
Если
0 <
< 900, то работа силы
на перемещении
положительна A > 0.
Если
= 900, то работа силы
на перемещении
равна нулю A = 0.
Если
900 <
< 1800, то работа силы
на перемещении
отрицательна A < 0.
Если
вектор силы
противоположно направлен перемещению тела
,
то угол между векторами
=
1800, следовательно работа силы
на перемещении
отрицательна и равна A = -
.
Задача. Определить работу силы тяжести при подъеме легкового автомобиля массой 1 тонна по трассе длинной 1 км, имеющей угол наклона 300 к горизонту.
Решение
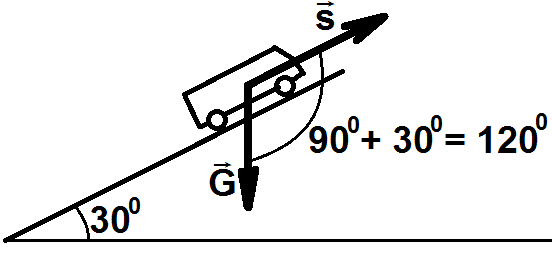
Работа
A силы тяжести
при перемещении тела
равна произведению длин векторов
и
на косинус угла между ними, то есть равна скалярному произведению
векторов силы тяжести и перемещения
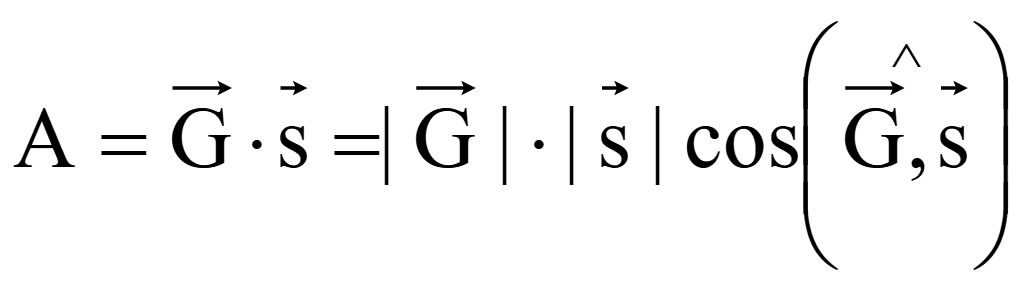
Сила тяжести
G = mg = 1000 кг · 10 м/с2 = 10 000 Н.
=
1000 м.
Угол
между векторами
=
1200. Тогда
cos 1200 = cos (900 + 300) = - sin 300 = - 0,5.
Подставляем
A = 10 000 Н · 1000 м · (-0,5) = - 5 000 000 Дж = - 5 МДж.
20 Скалярное произведение векторов в координатах
Скалярное
произведение двух векторов
= (x1; y1;
z1) и
= (x2; y2;
z2) в прямоугольной системе
координат равно сумме произведений одноименных координат
=
x1x2
+ y1y2
+ z1z2.
То есть скалярное произведение двух векторов равно сумме произведений одноименных координат.
21 Условие перпендикулярности векторов
Если
ненулевые векторы
= (x1; y1;
z1) и
= (x2; y2;
z2) перпендикулярны, то их
скалярное произведение равно нулю
=
0,
=
x1x2
+ y1y2
+ z1z2
= 0.
Если
задан один ненулевой вектор
= (x1; y1;
z1), то координаты
перпендикулярного (нормального) ему ненулевого
вектора
= (x2; y2;
z2) должны удовлетворять
равенству
x1x2 + y1y2 + z1z2 = 0.
Таких
векторов
бесконечное множество.
Если
на плоскости задан один ненулевой вектор
= (x1; y1),
то координаты перпендикулярного (нормального) ему вектора
= (x2; y2)
должны удовлетворять равенству
x1x2 + y1y2 = 0.
Отсюда можно выразить произведение координат y
y1y2 = - x1x2.
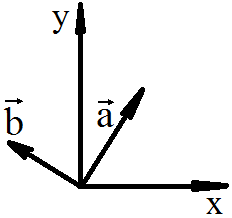
Если
на плоскости задан ненулевой вектор
= (x1; y1),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора
= (x2; y2)
и из условия перпендикулярности векторов
x1x2 + y1y2 = 0
выразить
вторую координату вектора
.
Например, если подставить произвольную координату x2, то из равенства
y1y2 = - x1x2
выражается
вторая координата вектора
Если
произвольно придать x2 = y1,
то вторая координата вектора
Если
на плоскости задан ненулевой вектор
= (x1; y1),
то перпендикулярный (нормальный) ему вектор
= (y1; -x1).
Если
одна из координат ненулевого вектора
равна нулю, то у перпендикулярного ему ненулевого вектора
такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если
= (0; y1),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор
= (x2;
0) лежит на оси Ox.
Определим
второй вектор, перпендикулярный вектору
= (x1; y1),
но противоположный вектору
= (y1; -x1),
то есть вектор -
.
Тогда достаточно поменять знаки координат вектора
-
= -1·
= (-1·y1;
-1·(-x1))=
(-y1; x1).
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
1
= (y1; -x1),
2
= (-y1; x1).
Для получения координат ненулевых векторов, перпендикулярных заданному ненулевому вектору на плоскости, достаточно поменять местами координаты заданного вектора и поменять знак одной из координат.
Задача.
Задан вектор
= (3; -5). Найти два нормальных вектора с различной ориентацией.
Решение
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
1
= (y1; -x1),
2
= (-y1; x1).
Подставляем
координаты вектора
= (3; -5)
1
= (-5; -3),
2
= (-(-5); 3) = (5; 3).
Для проверки перпендикулярности векторов подставим их координаты в условие перпендикулярности векторов
x1x2 + y1y2 = 0
3·(-5) + (-5)·(-3) = -15 + 15 = 0
верно!
3·5 + (-5)·3 = 15 - 15 = 0
верно!
Ответ:
1
= (-5; -3),
2
= (5; 3).
Если присвоить x2 = 1, подставить
x1 + y1y2 = 0.
y1y2 = -x1
Получим
координату y2 вектора,
перпендикулярного вектору
= (x1; y1)
Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору
= (x1; y1)
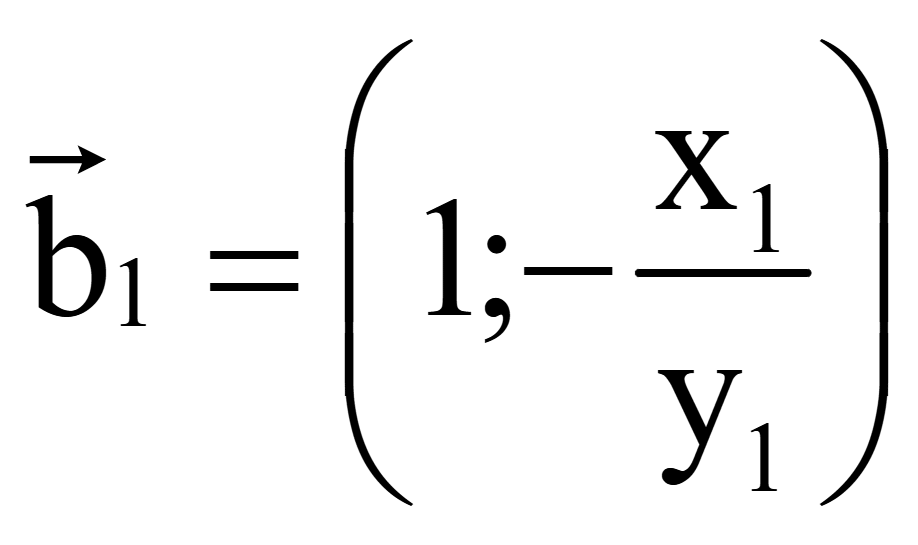
Для
получения второго вектора, перпендикулярного вектору
= (x1; y1),
но противоположно направленного вектору
.
Пусть
Тогда
достаточно поменять знаки координат вектора
.
Координаты
второго вектора, перпендикулярного на плоскости вектору
= (x1; y1)
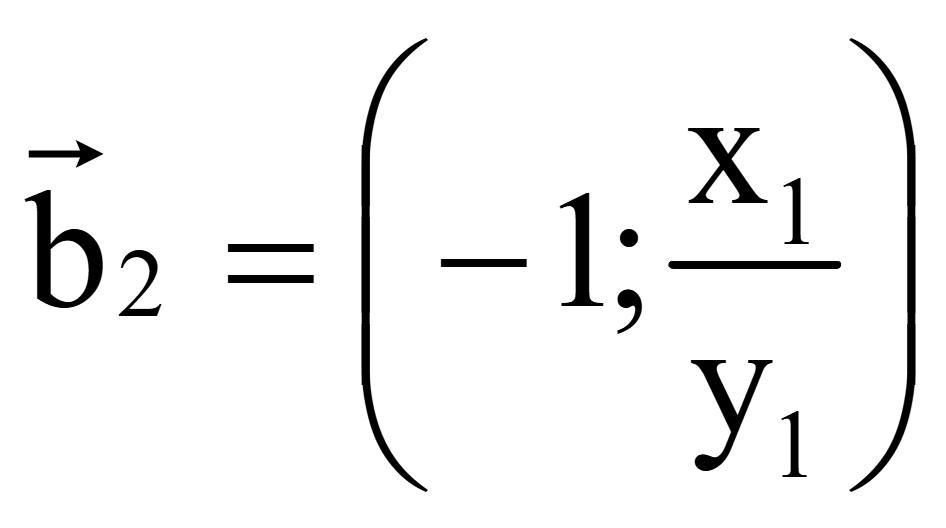
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
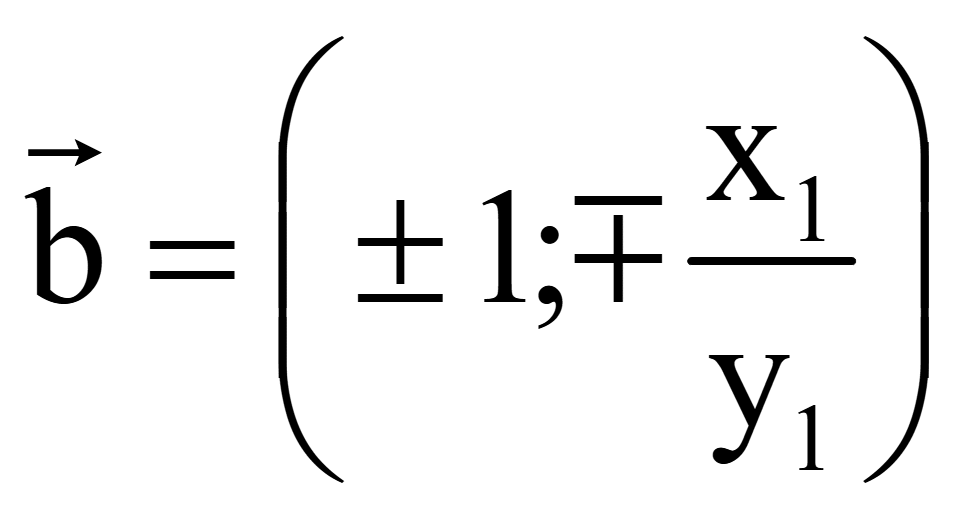
Задача.
Задан вектор
= (3; -5). Найти два нормальных вектора с различной ориентацией.
Решение
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
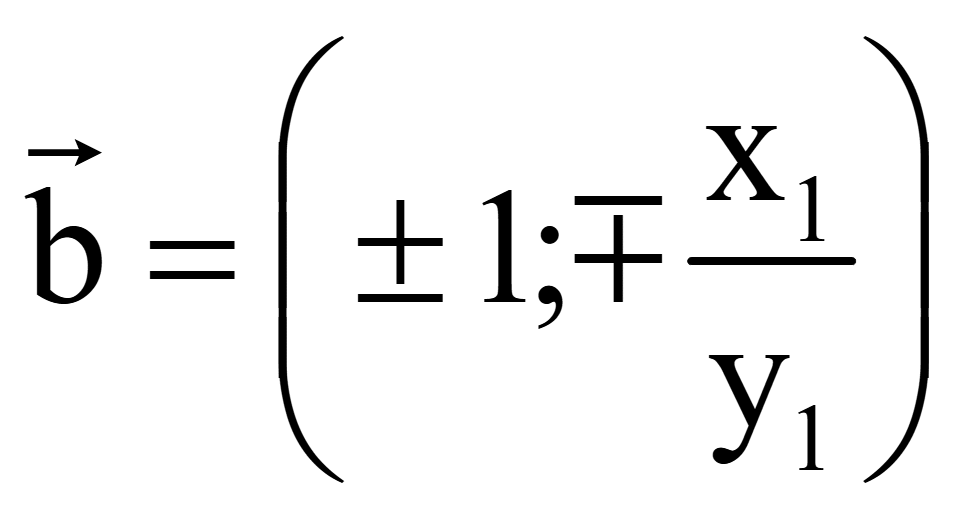
Координаты одного вектора
Координаты второго вектора
Для проверки перпендикулярности векторов подставим их координаты в условие перпендикулярности векторов
x1x2 + y1y2 = 0
3·1 + (-5)·0,6 = 3 - 3 = 0
верно!
3·(-1) + (-5)·(-0,6) = -3 + 3 = 0
верно!
Ответ:
и
.
Если присвоить x2 = - x1, подставить
x1(-x1) + y1y2 = 0.
-x12 + y1y2 = 0.
y1y2 = x12
Получим
координату вектора, перпендикулярного вектору
Если присвоить x2 = x1, подставить
x1x1 + y1y2 = 0.
x12 + y1y2 = 0.
y1y2 = -x12
Получим
координату y второго вектора,
перпендикулярного вектору
Координаты
одного вектора, перпендикулярного на плоскости вектору
= (x1; y1)
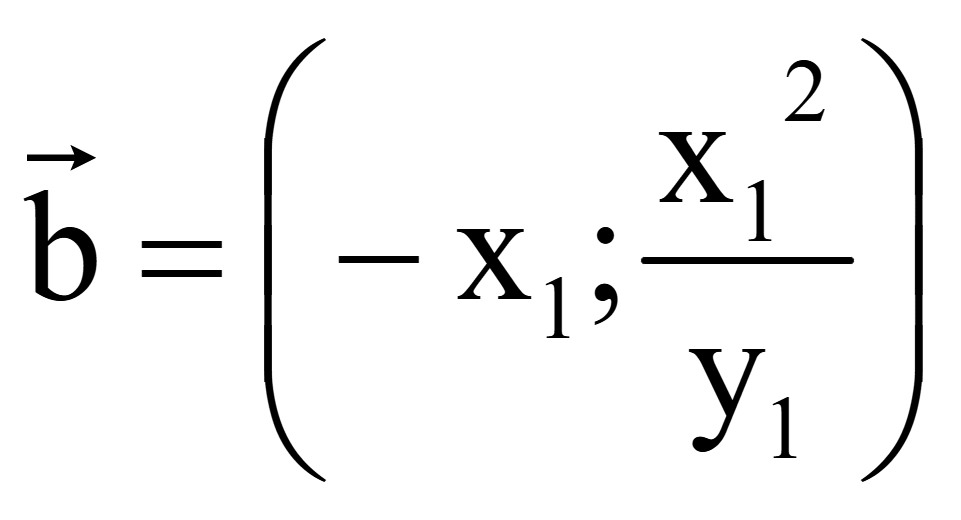
Координаты
второго вектора, перпендикулярного на плоскости вектору
= (x1; y1)
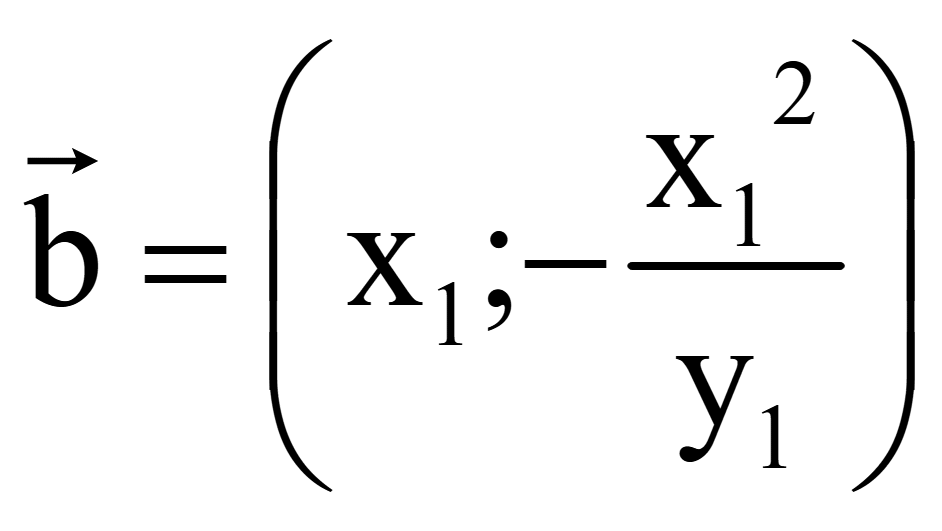
Координаты
двух векторов, перпендикулярных вектору
= (x1; y1)
на плоскости
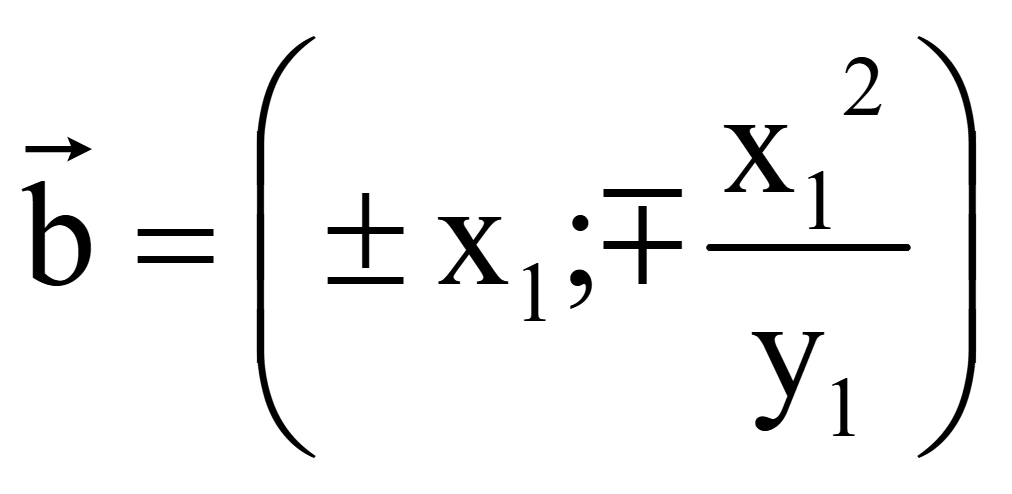
22 Нулевой вектор
Нулевой
вектор имеет длину равную нулю
= 0. Нулевой вектор имеет координаты равные нулю
(0;
0; 0). Нулевой вектор коллинеарен любому вектору. В частности,
нулевой вектор сонаправлен любому вектору. Произведение нулевого
вектора на любое число дает нулевой вектор. Если оба вектора нулевые,
то угол между нулевыми векторами равен 00.
Векторы на плоскости и в пространстве веб-страницы: 1 2 3
©