© 2021 Ольшевский Андрей Георгиевич репетитор по математике, физике, информатике, программированию, авиации, двигателям, электронике, искусственному интеллекту, техническим дисциплинам по Скайп da.irk.ru
Сайт super-code.ru с полезными темами, которые вы можете бесплатно сохранить
Оглавление
2 Знаки тригонометрических функций 7
3 Значения тригонометрических функций некоторых углов 9
4 Построение прямоугольного треугольника с углами 600 и 300 по клеточкам 11
5 Основное тригонометрическое тождество 12
6 Тригонометрические функции в прямоугольном треугольнике 12
8 Тригонометрические формулы 17
8.1 Тригонометрические функции суммы и разности аргументов 17
8.3 Формулы понижения степени 18
8.4 Сложение и вычитание функций 19
8.5 Преобразование произведения в сумму и разность 19
9 Обратные тригонометрические функции 20
10 Общие замечания об обратных тригонометрических функциях 22
11 Решение тригонометрических уравнений 23
11.1 Решение уравнения cos α = x 23
11.2 Решение уравнения sin α = y 27
11.3 Решение уравнения tg α = y 28
11.4 Решение уравнения ctg α = y 28
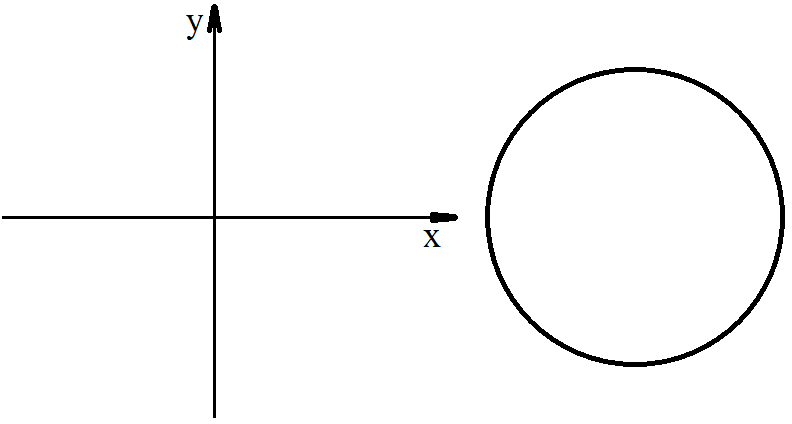
12 Шаблоны осей координат и окружностей 36
13 Список использованных источников 38
Алгебра 7, 8, 9, 10, 11 класс, определения и формулы
Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru
Тригонометрия переводится как «измерение треугольников». Изобразим окружность произвольного радиуса OR:
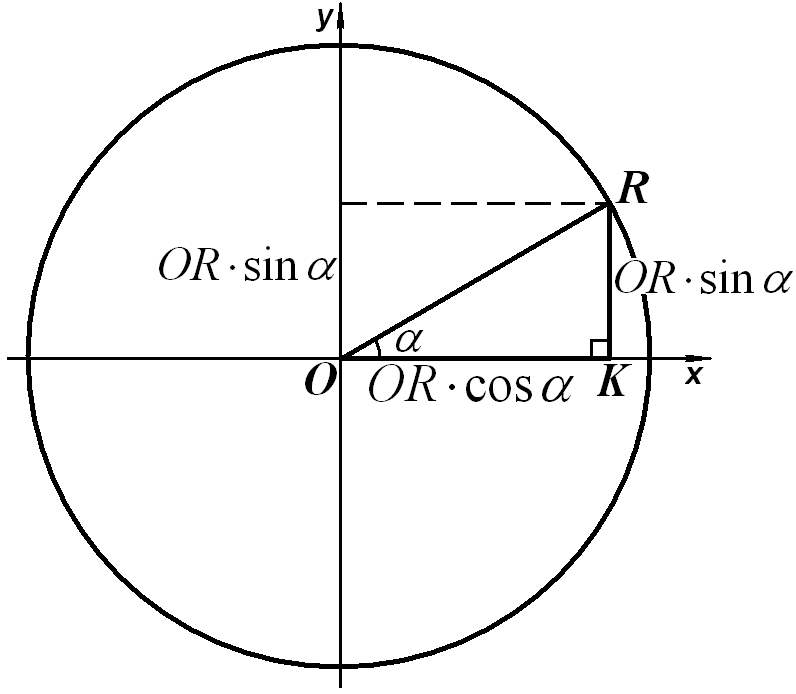
отсюда
катет ПРОТИВОлежащий = гипотенуза·sin α
RK = OR·sin α.
Синус переводится на английский как sine. Косинус переводится на английский как cosine. Слова отличаются приставкой «co».
Co – в английском языке приставка, обозначающая совместность, на русский язык переводится как приставка «со» (например, составляющий, соприкасающийся, совместный, сопряженный). Таким образом, функция cos своим названием указывает на то, что катет составляет угол. Функция cos созвучна слову «касается», поэтому
катет СОставляющий угол = гипотенуза·cos α
OK = OR·sin α.
У единичной окружности радиус r = 1, поэтому гипотенуза, равная радиусу также равна 1. Поэтому для единичной окружности
sinα = катету, ПРОТИВОлежащему углу α,
cosα = катету, СОставляющему угол α.
-1 ≤ sinα ≤ 1
-1 ≤ cosα ≤ 1
cos – четная функция, все остальные функции (sin, tg, ctg) – нечетные.
cos(-α) = cos α
sin(-α) = -sin α
tg(-α) = -tg α
ctg(-α) = -ctg α
Радиан - величина центрального угла, образующего на окружности дугу, длина которой равна радиусу окружности.
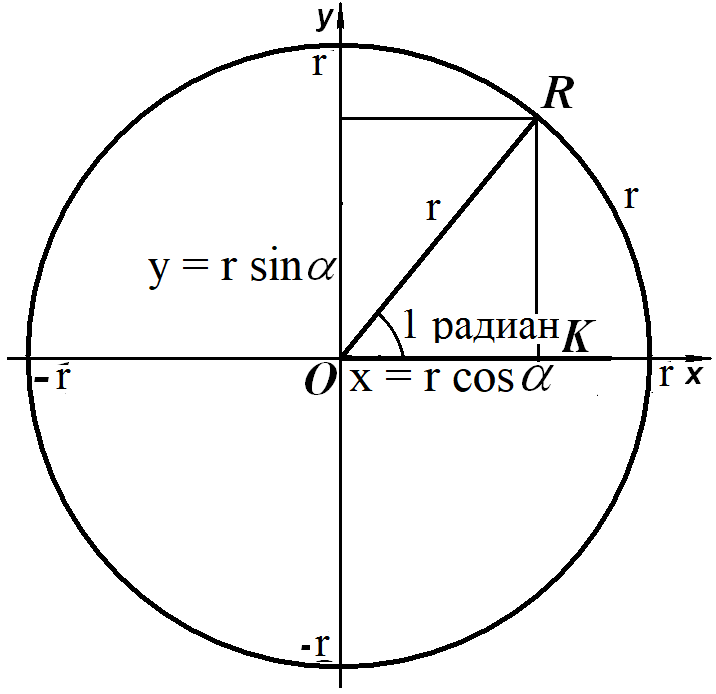
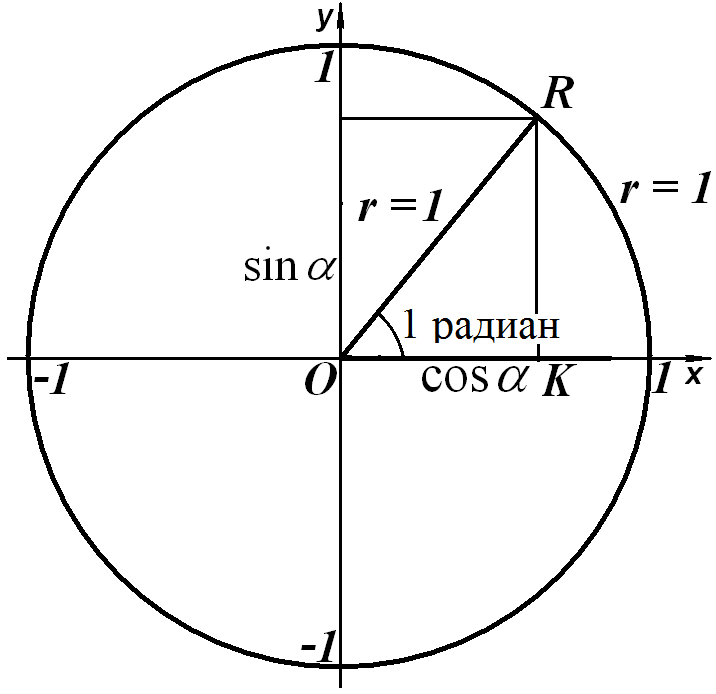
1800 = π радиан
Отсюда
cosec
α =
tgα·ctgα = 1
sin α
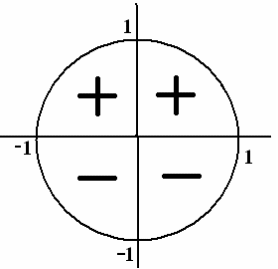
cos α
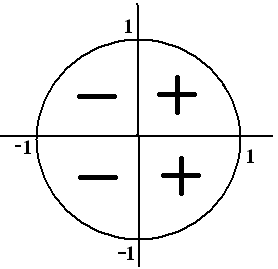
tg α
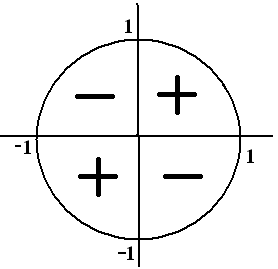
ctg α
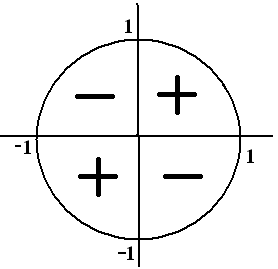
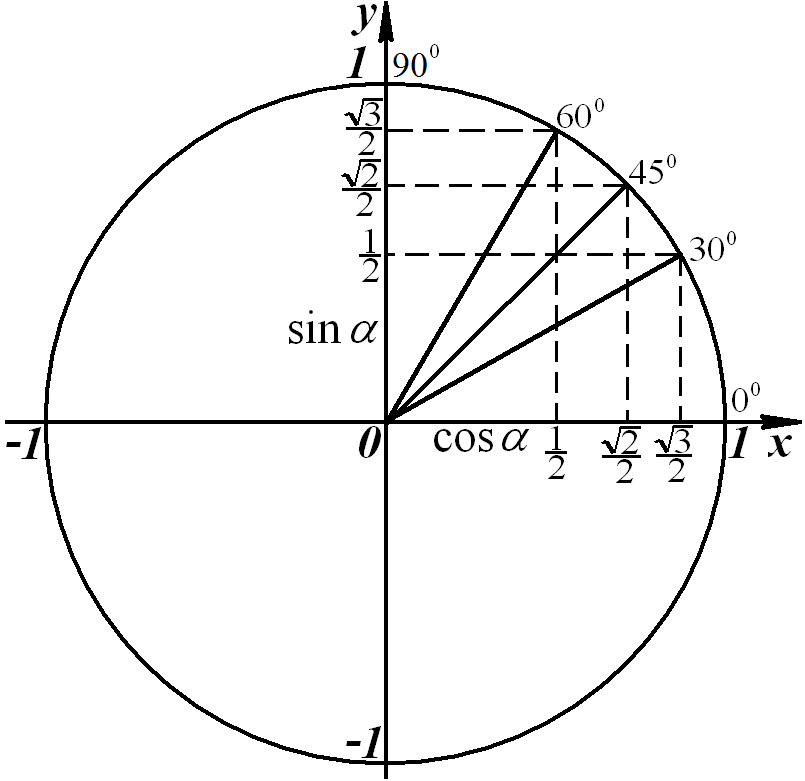
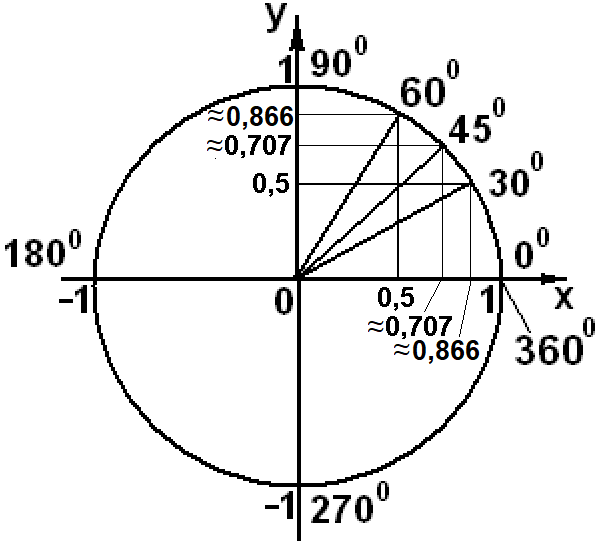
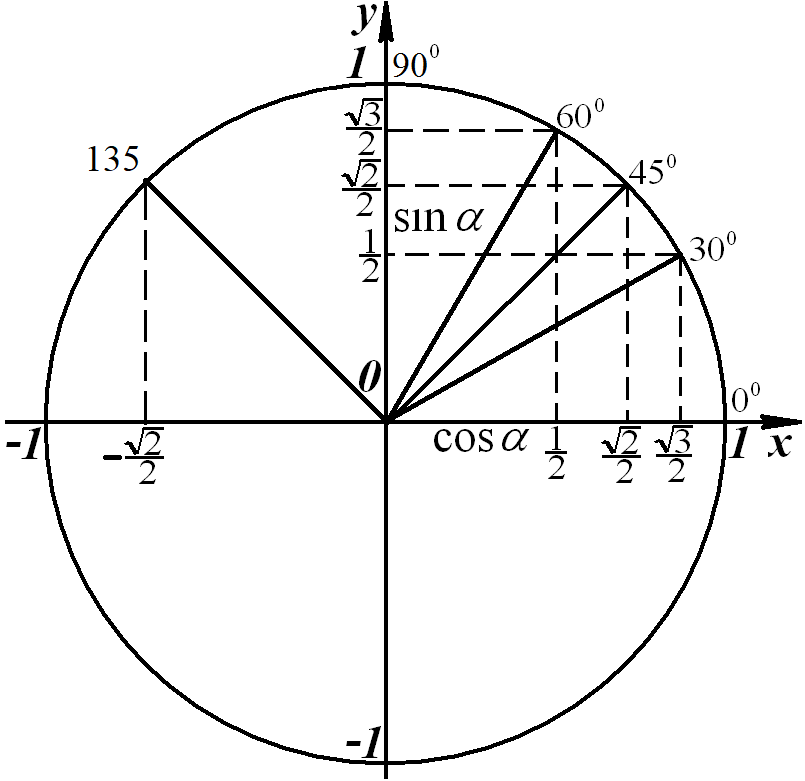
sin 00 = cos 900 = 0;
sin 900 = cos 00 = 1.
Из курса геометрии известно: «Катет, лежащий против угла 300, равен половине гипотенузы». Гипотенуза равна радиусу единичной окружности, т. е. 1, поэтому
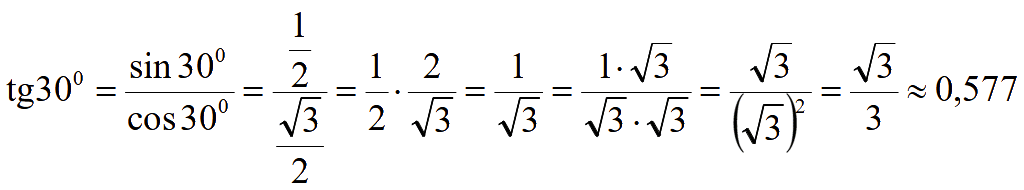
1800 = π
Прямоугольный треугольник, имеющий углы 600 и 300 может иметь гипотенузу 8, катер напротив угла 300 равен половине гипотенузы, то есть 4 и катет напротив угла 600 равен
8·sin 600 ≈ 8·0,866 ≈ 6,9282 ≈ 7.
Прямоугольный треугольник с катетами 4 и 7 имеет гипотенузу примерно 8 и углы примерно 600 и 300. Его удобно строить по клеточкам при решении задач.
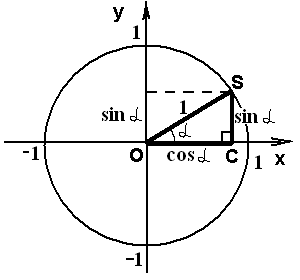
В прямоугольном треугольнике OCS гипотенуза OS = 1 (радиус единичной окружности), катет OC = cosα, катет CS = sinα. По теореме Пифагора
12 = sin2α + cos2α.
Основное тригонометрическое тождество
sin2α + cos2α = 1;
sin2α = 1 – cos2α;
cos2α = 1 - sin2α;
.
,
,
.
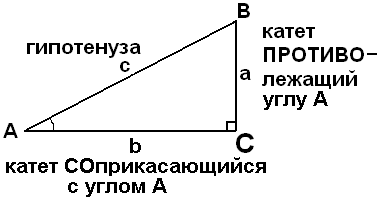
катет ПРОТИВОлежащий = гипотенуза·sin A;
катет СОставляющий угол = гипотенуза·cos A;
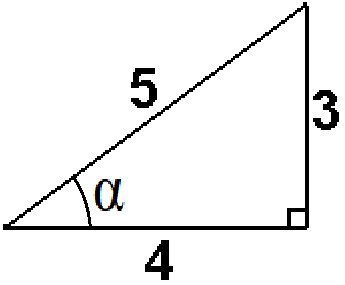
Египетский треугольник с соотношением сторон 3:4:5 является прямоугольным
Проверим выполнение основного тригонометрического тождества
sin2α + cos2α = 1
0,62 + 0,82 = 0,36 + 0,64 = 1
Для египетского треугольника выполняется теорема Пифагора:
52 = 32 + 42;
25 = 9 + 16.
Если стороны треугольника имеют соотношения сторон 3r : 4r : 5r (r > 0), то треугольник также является прямоугольным
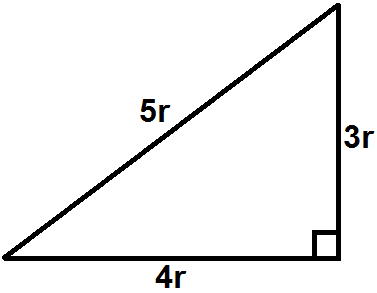
(5r)2 = (3r)2 + (4r)2;
52·r2 = 32·r2 + 42·r2;
r2·52 = r2·(32 + 42);
52 = 32 + 42;
25 = 9 + 16.
Пример.
Формулы приведения позволяют упростить аргумент тригонометрической функции с целью получения тригонометрической функции угла, при котором тригонометрическая функция вычисляется, или значительно упрощается.
Если угол α прибавляется или отнимается от угла, содержащего целое число значений π, то тригонометрическая функция сохраняется, а угол упрощается до α. Если угол α прибавляется или отнимается от угла, содержащего целое число значений π/2, то тригонометрическая функция меняется на кофункцию (sin-cos, tg-ctg), а угол упрощается до α. Принимается знак, который имела бы первоначальная функция при остром угле α.
Тригонометрическая функция угла α или выражения с углом α, отложенного на единичной окружности, соответствует какому-то значению на оси Ox для функции cos или на оси Oy для функции sin. Если угол α выбрать близким к нулю, то отрезок на оси Ox, равный cosα будет значительно больше отрезка на оси Oy, равного sinα. Это позволяет по длине равных отрезков на координатной оси установить однозначное соответствие между значениями тригонометрических функций углов 1800 - α, 1800 + α, 900 - α, 900 + α и тригонометрическими функциями угла α с учетом знаков на координатных осях.
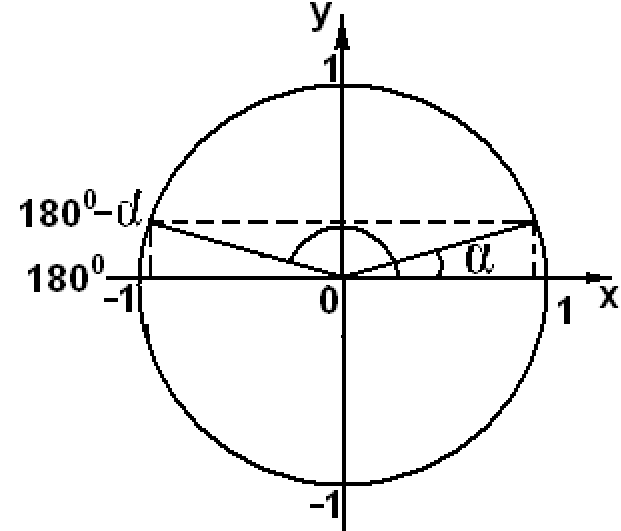
sin(1800 - α) = sinα
sin(π - α) = sinα
cos(1800 - α) = - cosα
cos(π - α) = - cosα
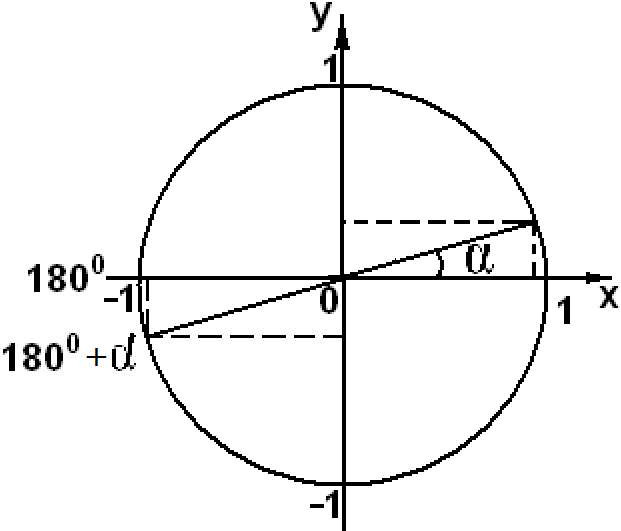
sin(1800 + α) = - sinα
sin(π + α) = - sinα
cos(1800 + α) = - cosα
cos(π + α) = - cosα
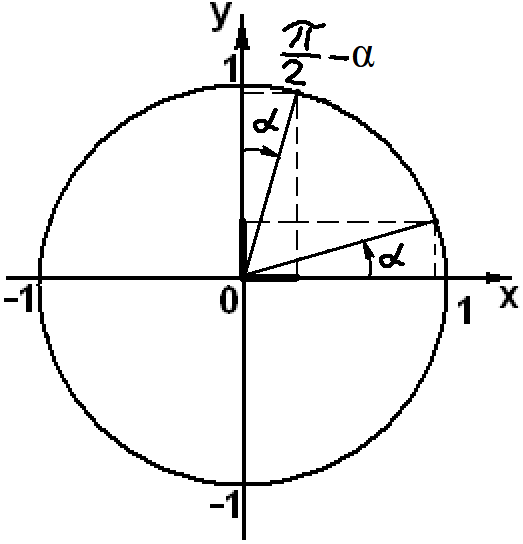
sin(π/2 - α) = cosα
sin(900 - α) = cosα
cos(π/2 - α) = sinα
cos(900 - α) = sinα
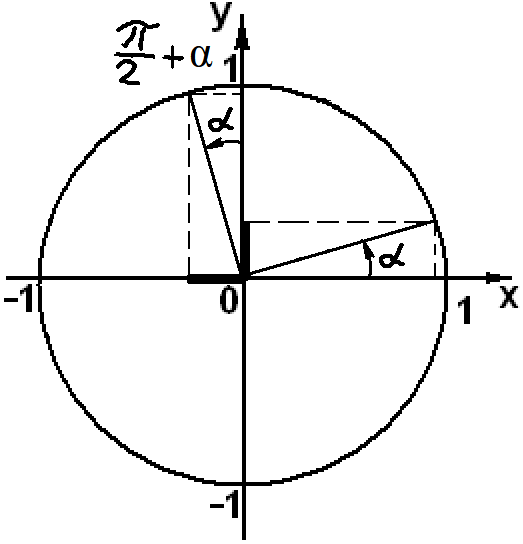
sin(π/2 + α) = cosα
sin(900 + α) = cosα
cos(π/2 + α) = - sinα
cos(900 + α) = - sinα
sin(α + β) = sin α cos β + cos α sin β
sin(α - β) = sin α cos β - cos α sin β
cos(α + β) = cos α cos β - sin α sin β
cos(α - β) = cos α cos β + sin α sin β
Объединим формулы суммы и разности аргументов
sin(α ± β) = sin α cos β ± cos α sin β;
cos(α ± β) = cos α cos β ∓ sin α sin β;
sin2α = 2 sin α cos α
cos2α = cos2α – sin2α = 1 - 2sin2α = 2cos2α – 1
cos2α = 2cos2α – 1;
cos2α + 1 = 2cos2α;
2cos2α = cos2α + 1;
cos2α = cos2α - sin2α = (1 - sin2α) - sin2α = 1 - 2sin2α;
cos2α = 1 - 2sin2α;
2sin2α = 1 - cos2α;
2α = β;
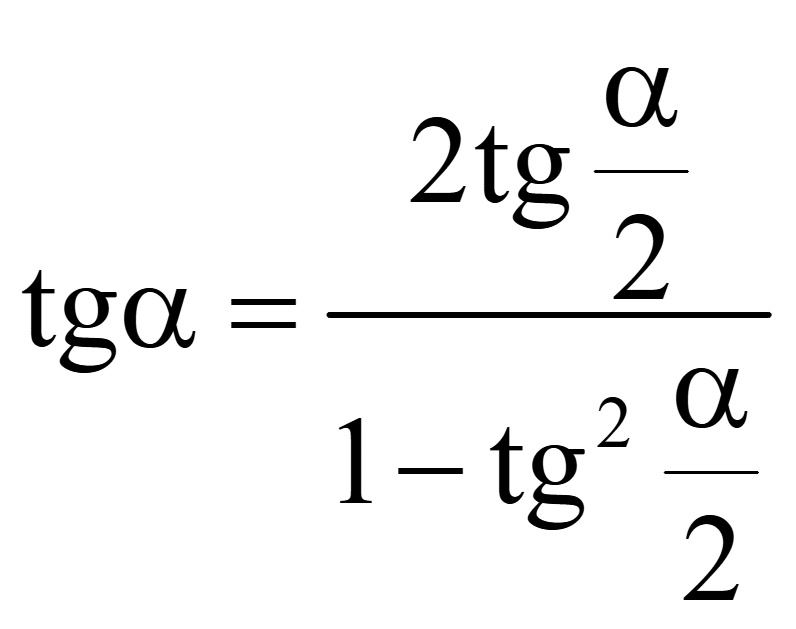
Эти же формулы, записанные в одну строку
tg 2α = 2tgα / (1 - tg²α);
tgα = 2tg (α/2)) / (1 - tg² (α/2)).
Если α + β = 900, то
tgα·tgβ = 1
Докажем это
Пример. Найти значение тригонометрического выражения
-49tg70·tg830 + 34.
Решение
Если α + β = 900, то
tgα·tgβ = 1
-49tg70·tg830 + 34 = -49·1 + 34 = -15.
Функция
y = arcsin x
обратная к функции y = sin
x, x ϵ
.
Функция y = arcsin
x обладает свойствами:
1. Область определения D(f) = [-1; 1].
2.Область
значений E(f) =
.
3. Функция y = arcsin x нечетная: arcsin (-x) = -arcsin x.
4. Функция y = arcsin x возрастает.
5. Функция y = arcsin x непрерывна.
При
x ϵ [-1; 1], y
ϵ
y = arcsin x
эквивалентно x = sin
y. Подстановка одной функции в другую и
наоборот, дают равенства
y = arcsin (sin y)
x = sin (arcsin x)
arcus - в переводе с латинского дуга (часть окружности, похоже на слово арка).
Функция y = arccos x обратная к функции y = cos x при x ϵ [0; π]. Функция y = arccos x обладает свойствами:
1. Область определения D(f) = [-1; 1].
2. Область значений E(f) = [0; π].
3. Функция y = arccos x не является ни четной, ни нечетной. Это функция общего вида.
4. Функция y = arccos x убывает.
5. Функция y = arccos x непрерывна.
На области определения функции y = arccos x справедивы равенства
cos (arccos x) = x;
arccos (-x) = π - arccos x.
arcus - в переводе с латинского дуга (часть окружности, похоже на слово арка).
Задача. Найти область определения функции
Решение
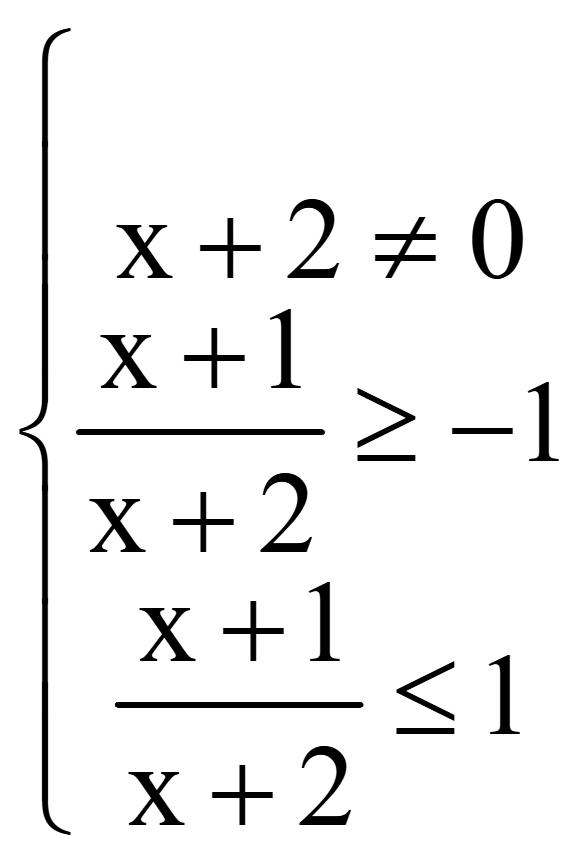
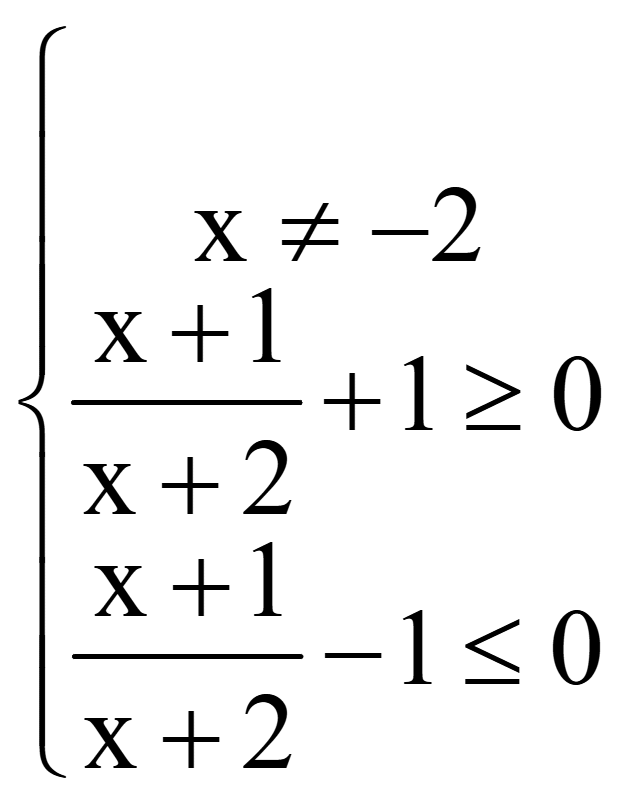
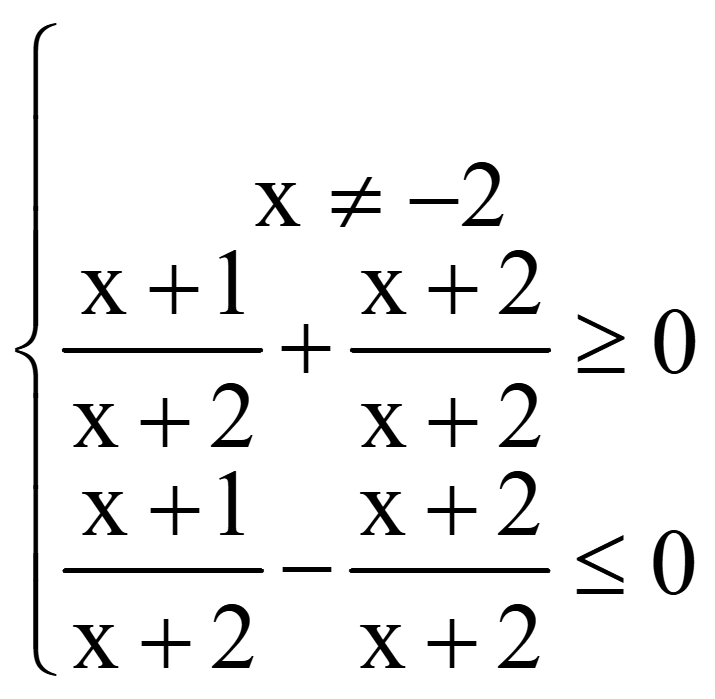
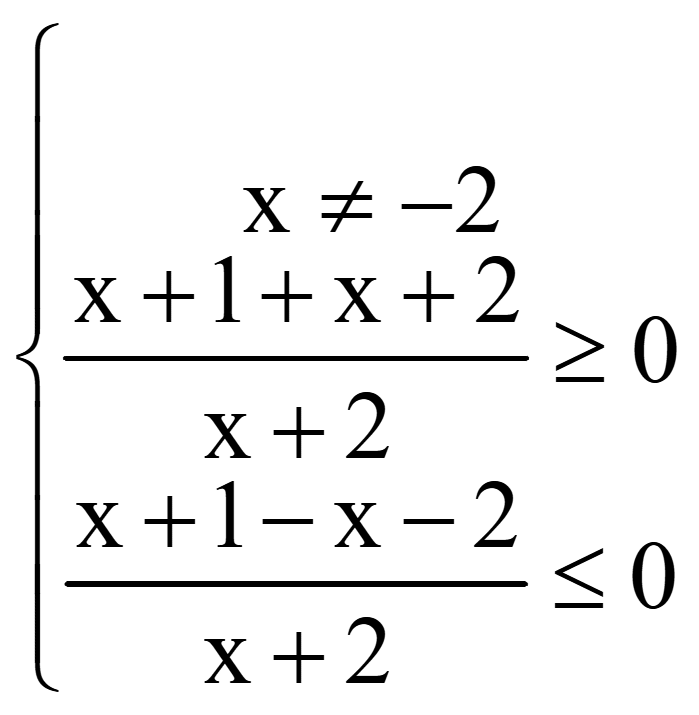
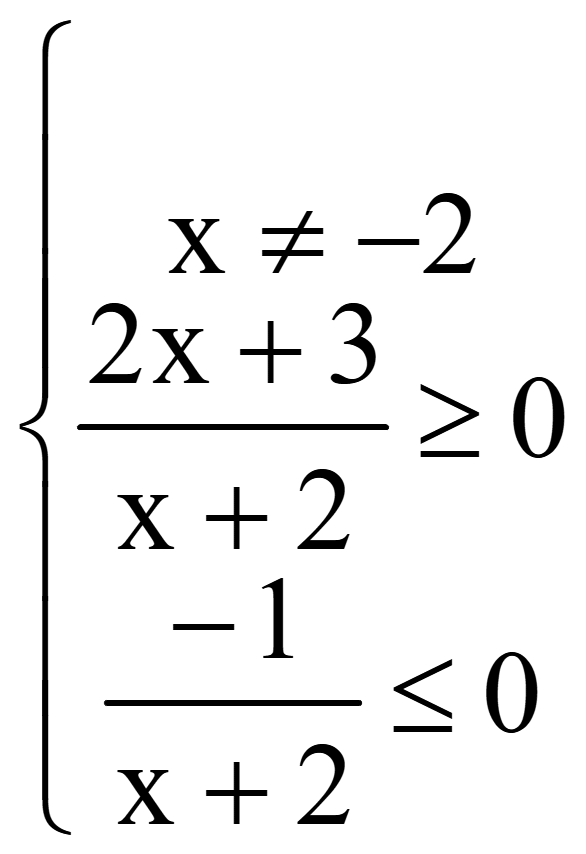
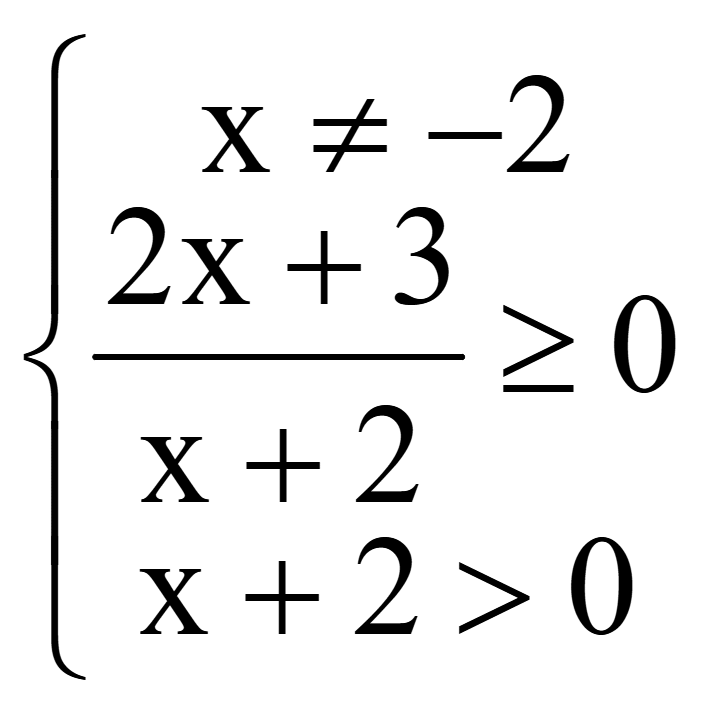
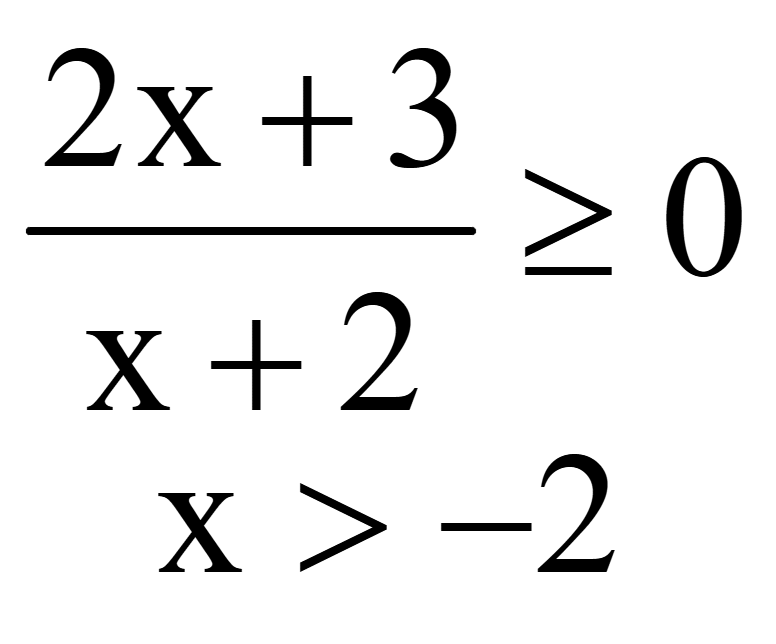
Методом интервалов решим 2-е неравенство
Ответ: x ϵ [-1,5; +∞).
Функция
y = arctg x
обратная к функции y = tg
x, x ϵ
.
Функция y = arctg
x обладает свойствами:
1. Область определения D(f) = (-∞; +∞).
2.Область
значений E(f) =
.
3. Функция y = arctg x нечетная: arctg (-x) = -arctg x.
4. Функция y = arctg x возрастает.
5. Функция y = arctg x непрерывна.
При
x ϵ (-∞;
+∞),
y ϵ
y = arctg x
эквивалентно x = tg
y. Подстановка одной функции в другую и
наоборот, дают равенства
y = arctg (tg y)
для любого числа x
x = tg (arctg x)
Функция y = arcctg x обратная к функции y = ctg x при x ϵ (0; π). Функция y = arcctg x обладает свойствами:
1. Область определения D(f) = (-∞; +∞).
2.Область значений E(f) = (0; π).
3. Функция y = arcctg x не является ни четной, ни нечетной. Это функция общего вида.
4. Функция y = arcctg x убывает.
5. Функция y = arcctg x непрерывна.
На области определения функции y = arcctg x, то есть для любого x справедливы равенства
tg ( arcctg x) = x.
Функции y = arcsin x и y = arctg x – нечетные. Функции y = arccosx и y = arcctg x не являются ни четными, ни нечетными. Это функции общего вида.
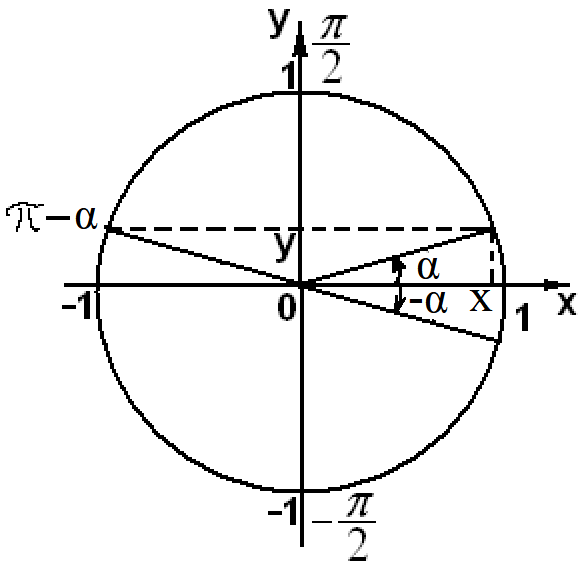
Если необходимо найти угол α при известном x, то решением уравнения
cosα = x
при α ϵ (-∞; +∞) будет в виде
α = Arccosx
на отрезке [0; π] α = arccosx. При α ϵ (-∞; +∞) получается совокупность решений
;
где n ϵ Z.
Общее решение
α = ±arccosx + 2πn, где n ϵ Z.
Задача. Решить уравнение cos α = 1
Решение
α = ±arccos1 + 2πn, где n ϵ Z;
α = ±0 + 2πn;
α = 2πn.
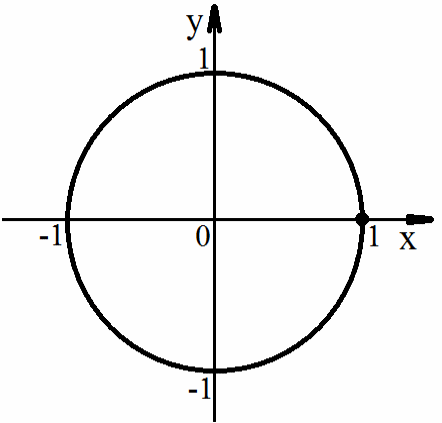
Ответ: α = 2πn, где n ϵ Z.
Задача. Решить уравнение cosα = 0
Решение
α = ±arccos0 + 2πn, где n ϵ Z;
α = ±π/2 + 2πn;
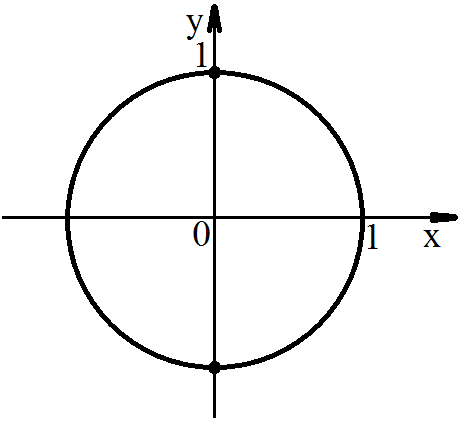
Через каждые полоборота углы удовлетворяют решению задачи, поэтому запишем более простое решение:
α = π/2 + πn.
Ответ: α = π/2 + πn, где n ϵ Z.
Задача. Решить уравнение cosα = -1
Решение
α = ±arccos(-1) + 2πn, где n ϵ Z;
α = ±π + 2πn;
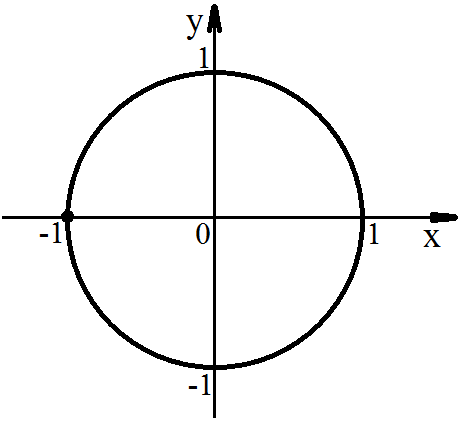
Расстояние между углами π и - π один оборот, то есть 2π, поэтому решение будет в виде:
α = π + 2πn.
Ответ: α = π + 2πn, где n ϵ Z.
Задача. Решить уравнение cosα = 0,5.
Решение
α = ±arccos0,5 + 2πn, где n ϵ Z;
α = ±π/3 + 2πn;
Ответ: α = ±π/3 + 2πn, где n ϵ Z.
Задача.
Решить уравнение
.
Решение
α
= ±
+ 2πn, где n ϵ
Z;
α = ±π/6 + 2πn;
Ответ: α = ±π/6 + 2πn, где n ϵ Z.
Задача.
Решить уравнение
.
Решение
α
= ±
+ 2πn, где n ϵ
Z;
α = ±π/4 + 2πn;
Ответ: α = ±π/4 + 2πn, где n ϵ Z.
Задача.
Решить уравнение
.
Решение
α
= ±
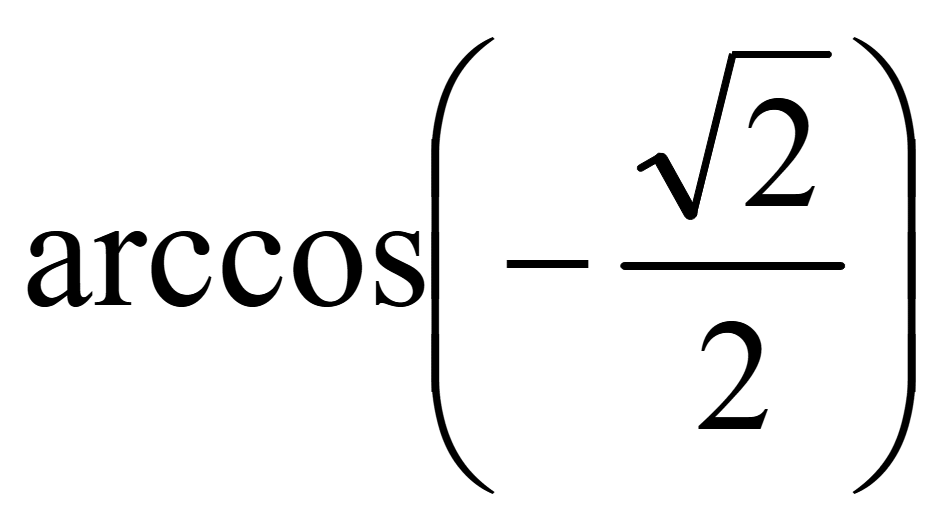+ 2πn, где n ϵ
Z;
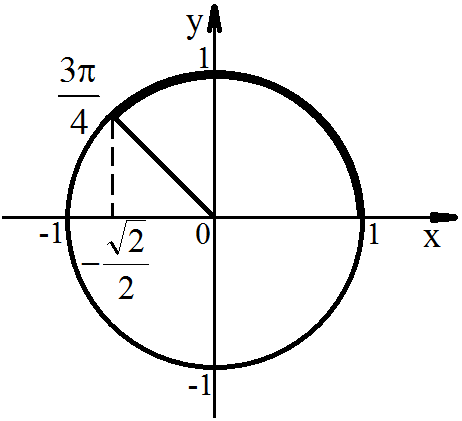
α
= ±
+ 2πn;
Ответ:
α = ±
+ 2πn, где n ϵ
Z.
Если необходимо найти угол α при известном y, то решением уравнения
sin α = y
При α ϵ (-∞; +∞)
α = Arcsiny
на отрезке [-π/2; π/2] α = arcsin y. При α ϵ (-∞; +∞) получается совокупность решений
;
;
,
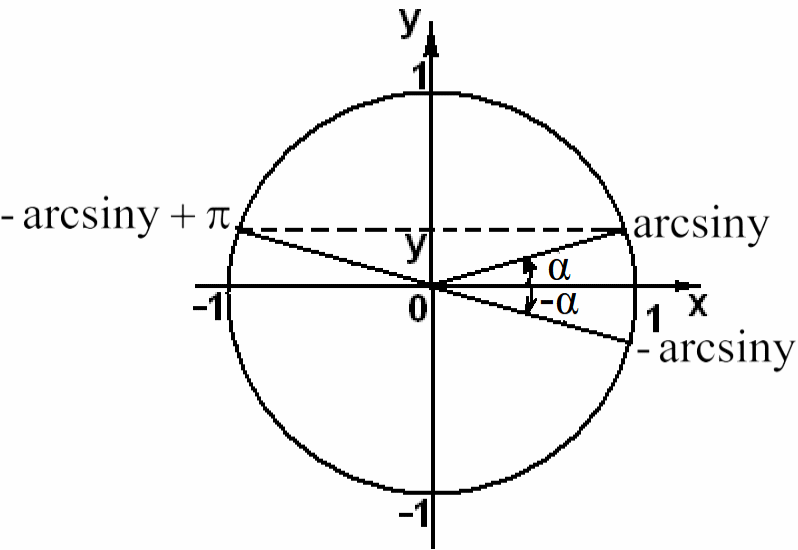
но 2n — четное число и в этом случае перед arcsiny минус отсутствует. (2n + 1) — нечетное число и перед arcsiny стоит минус. Поэтому можем записать для четных и нечетных k одну формулу:
α = (-1)karcsiny + πk, k ϵ Z.
Когда k – четное (-1) в четной степени равна единице и перед arcsiny минуса не будет, если k – нечетное (-1) в нечетной степени дает (-1) и перед arcsiny получится минус.
Если необходимо найти угол α при известном y, то решением уравнения
tg α = y
будет
α = arctg y + πn, n ϵ Z.
Если необходимо найти угол α при известном y, то решением уравнения
ctg α = y
будет
α = arcctg y + πn, n ϵ Z.
Задача. Для заданного
.
Найти cosα.
Решение
sin2α + cos2α = 1;
cos2α = 1 - sin2α;
.
Так как угол принадлежит первой координатной четверти, то косинус этого угла положительный
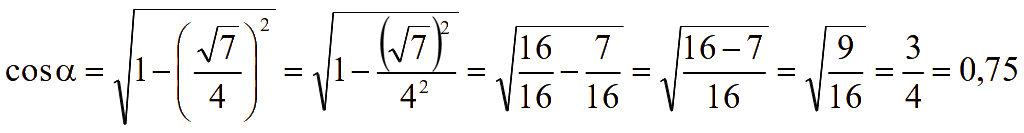
Ответ: cosα = 0,75.
Пример. Решите уравнение
и укажите корни уравнения на отрезке [-π; 2π].
Решение
Найдем корни уравнения на отрезке [-π; 2π].
Разделим на π все части неравенства
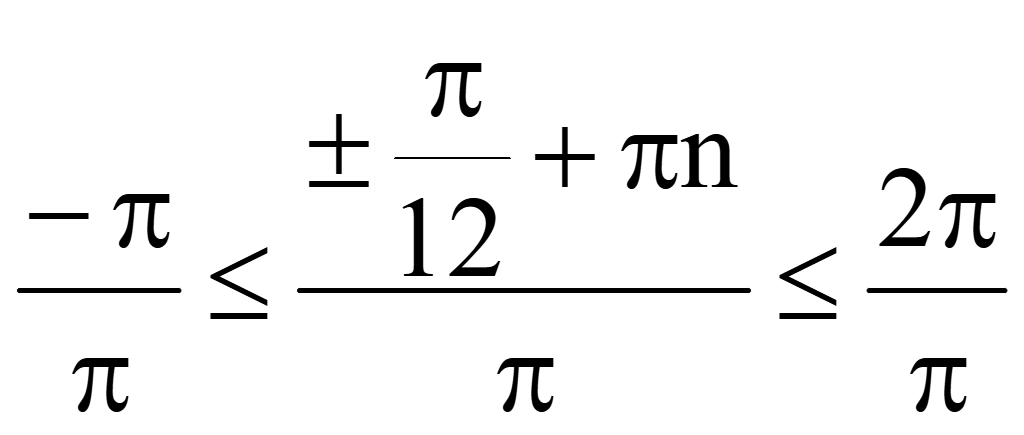
-12 ≤ ±1+12n ≤ 24
Для оценки значений n уберем ±1
-12 ≤ 12n ≤ 24;
-1 ≤ n ≤ 2;
Выражение
при n = -2 значения меньше заданного отрезка [-π; 2π].
При n = -1
При n = 0
При n = 1
При n = 2
Ответ:
.
6 корней уравнения на промежутке [-π; 2π]:
.
Пример. Решите уравнение
3sin2x + ctg2x sin2x - 2 = 0
и укажите корни уравнения на отрезке
.
Решение
3sin2x + cos2x = 2;
3sin2x + 1 - sin2x = 2;
2sin2x = 1;
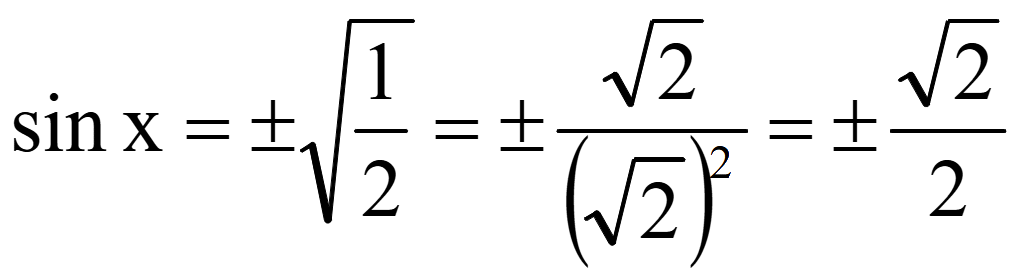
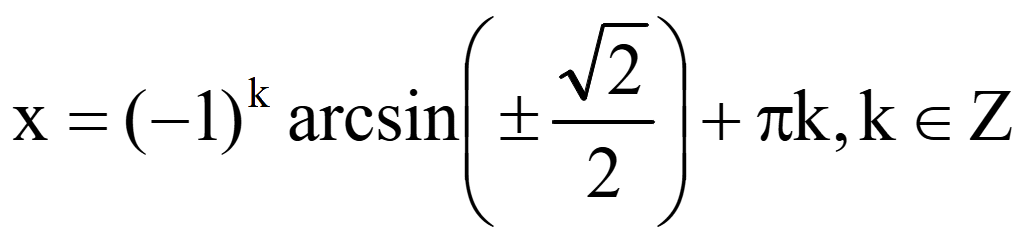
Функция нечетная: arcsin (-x) = -arcsin x, поэтому вынесем ± за arcsin
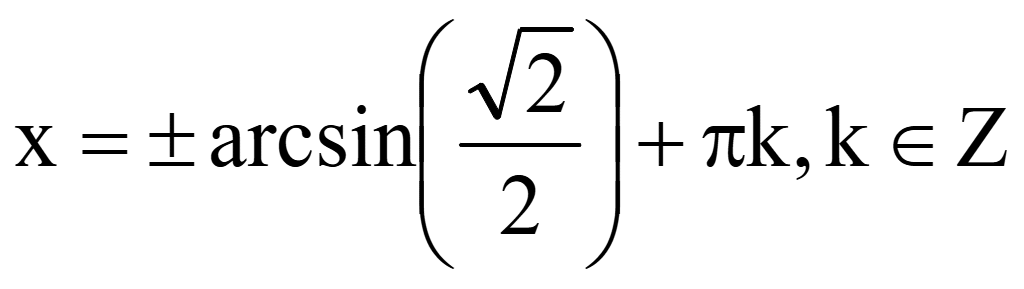
Выберем
корни уравнения на промежутке
.
.
Ответ:
.
3 корня уравнения на промежутке
.
Пример. Решите уравнение
Решение
ОДЗ:
.
Исходное уравнение равно нулю тогда, когда числитель равен нулю
Подстановка для упрощения уравнения t = cosx
Обратная замена переменной t
,
но корень
не удовлетворяет области определения, поэтому остается корень
.
Ответ:
.
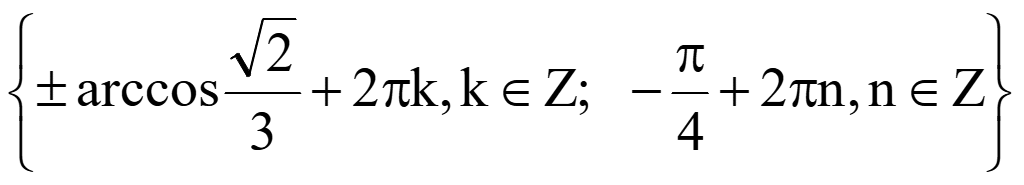Пример. Решите уравнение
Решение
ОДЗ:
Исходное уравнение равно нулю тогда, когда числитель равен нулю
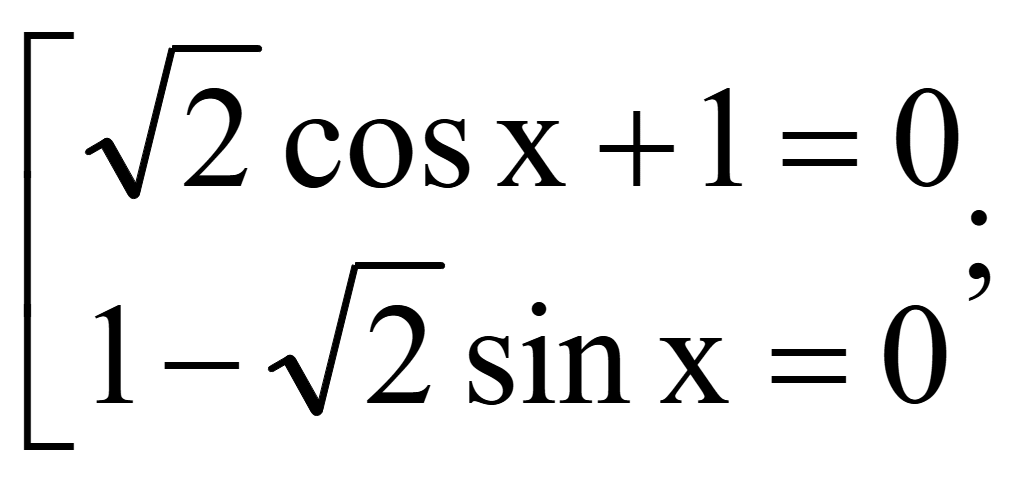
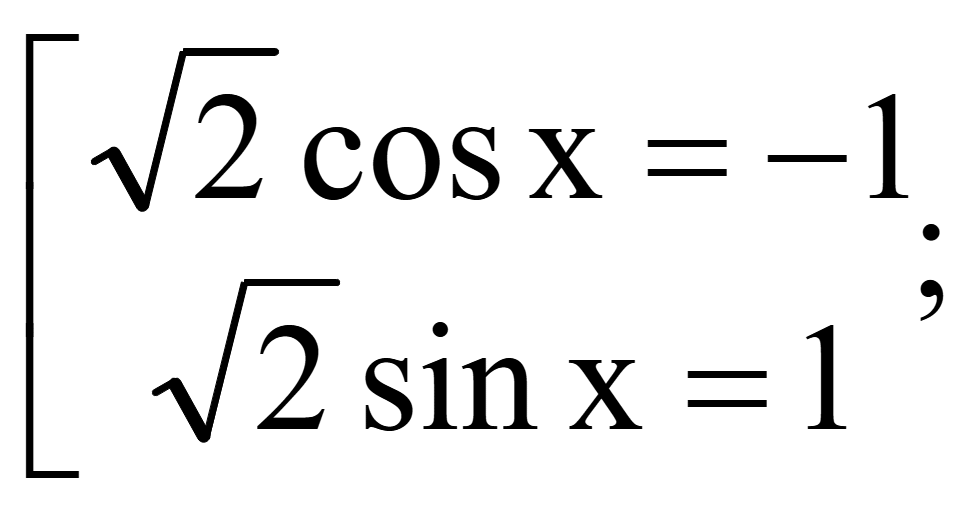
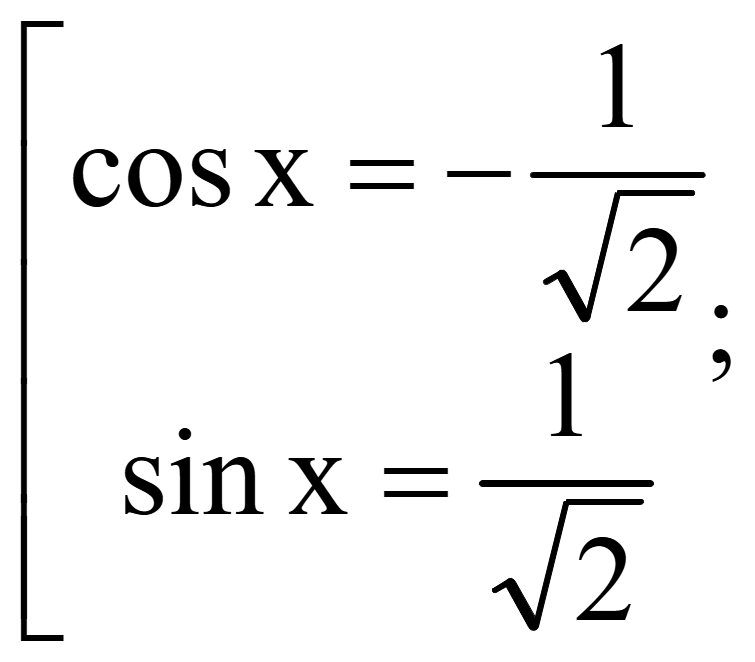
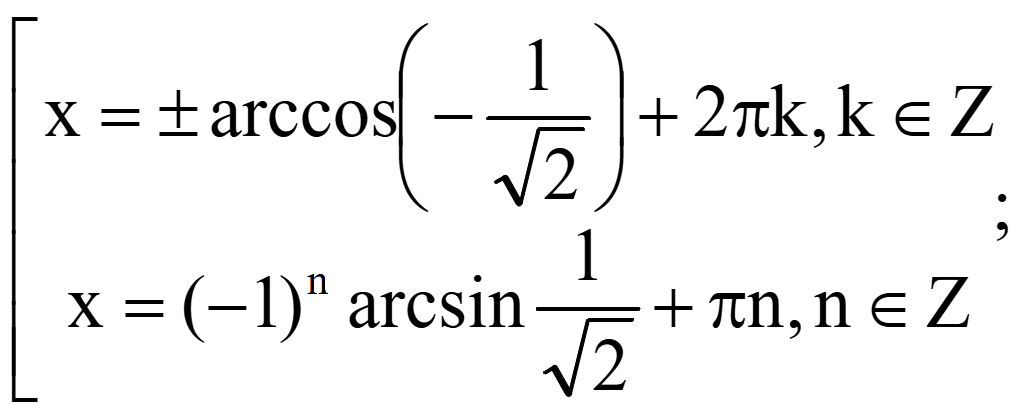
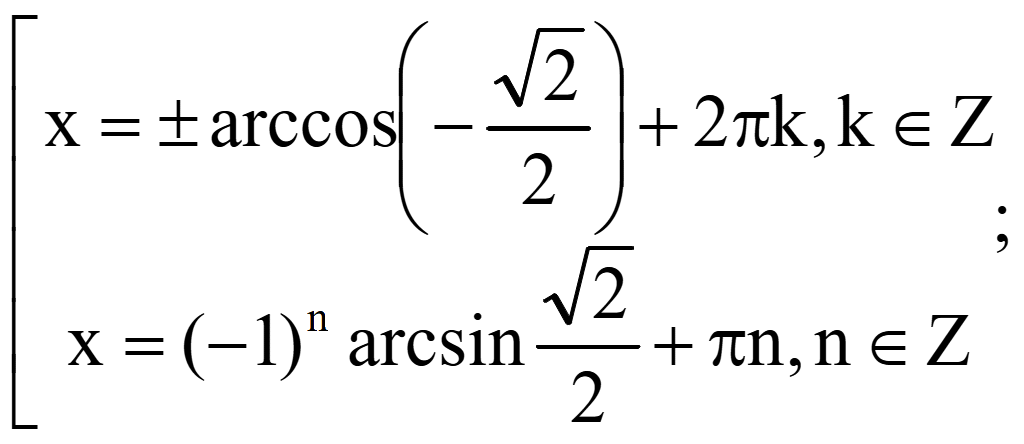
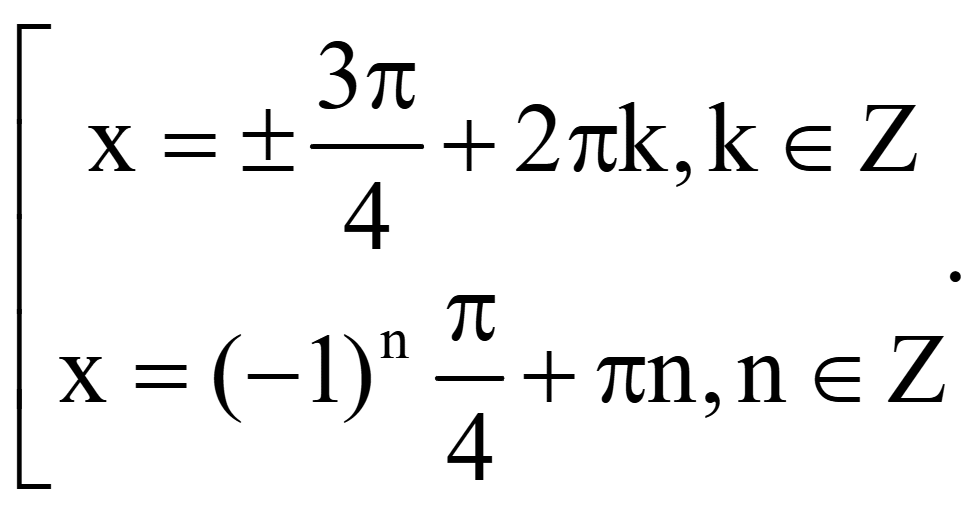
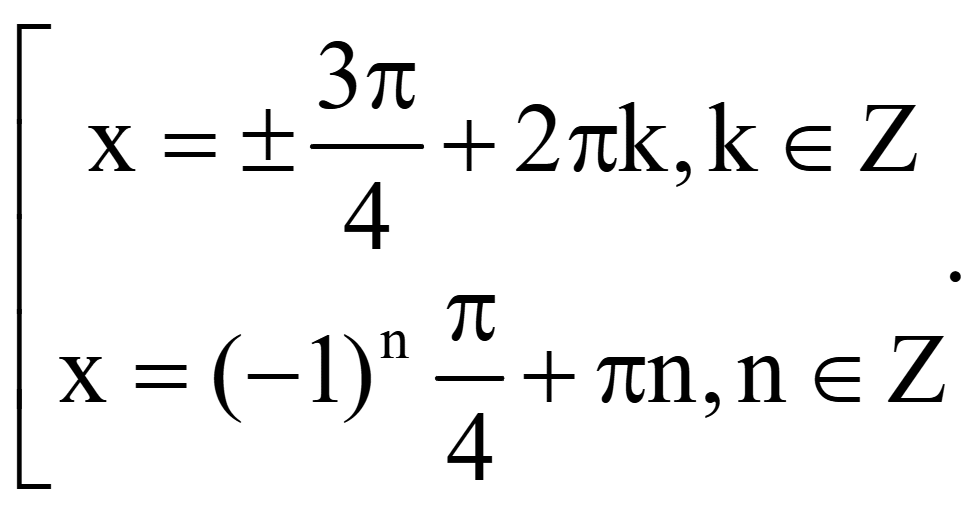
Пример. Решить уравнение
Решение
sin2α + cos2α = 1
sin2α = 2sinαcosα
Помножим на 2
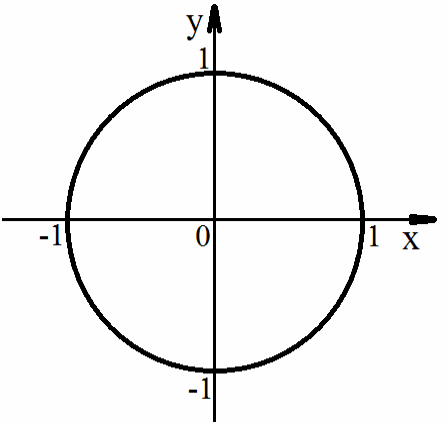
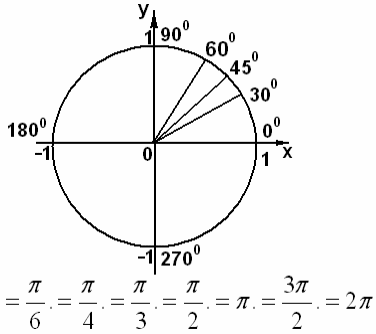
1. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. - М.: Мнемозина, 2009. - 424 с.
© 18.05.2021 Ольшевский Андрей Георгиевич e-mail: da.irk.ru@mail.ru
