© Ольшевский Андрей Георгиевич
Консультирую по скайп: da.irk.ru
Сайт super-code.ru наполняется бесплатными книгами
Дискретная математика, способы решения задач, примеры, теория, программы на С++
Оглавление
1.1 Логические операции в порядке убывания приоритета 3
1.2 Приоритет логических операций 3
2 Диаграммы Венна или в некоторых источниках Виенна, или Эйлера-Венна 4
3 Графы 5
3.1 Радиус, диаметр и центры графа 5
3.3 Остов минимального веса. Алгоритм Крускала 11
4 Элементы теории кодирования. Схема кодирования и декодирования 12
6 Граница Синглтона линейного кода 13
Список использованных источников с моими комментариями 15
Консультации Ольшевского Андрея Георгиевича по Skype da.irk.ru 17
Алгебра логики
Логические операции в порядке убывания приоритета
1.Инверсия (логическое отрицание) - логическая операция, которая данное высказывание преобразует в противоположное высказывание. Обозначается словами или символами: НЕ, NOT, , ¬, верхнее подчеркивание ().
Например: НЕ A, NOT A, , ¬A.
2.Конъюнкция (логическое умножение) обозначается словами или символами: И, AND, &, ·, *, ˄, ∏, ∩.
Например: A И B, A AND B, A & B, A · B, A * B, A ˄ B, A ∏ B, A ∩ B.
∩ - математический знак, обозначающий пересечение.
3.Дизъюнкция (логическое сложение) обозначается словами или символами: ИЛИ, OR, +, ˅, U, ∑.
Например: A ИЛИ B, A OR B, A + B, A ˅ B, A U B.
U - математический знак, обозначающий объединение.
4.Импликация (если A, то B) обозначается символами: =>, →.
5.Эквиваленция (A тогда и только тогда, когда B) обозначается словами или символами: <=>, ↔, ~, ≡.
Приоритет логических операций
Порядок выполнения логических операций определяют круглые скобки и порядок логических операций. Сначала выполняется операция отрицания (“не”), за ней - конъюнкция (“и”), затем — дизъюнкция (“или”), затем — импликация (→) и в последнюю очередь — эквивалентность ≡.
Диаграммы Венна или в некоторых источниках Виенна, или Эйлера-Венна
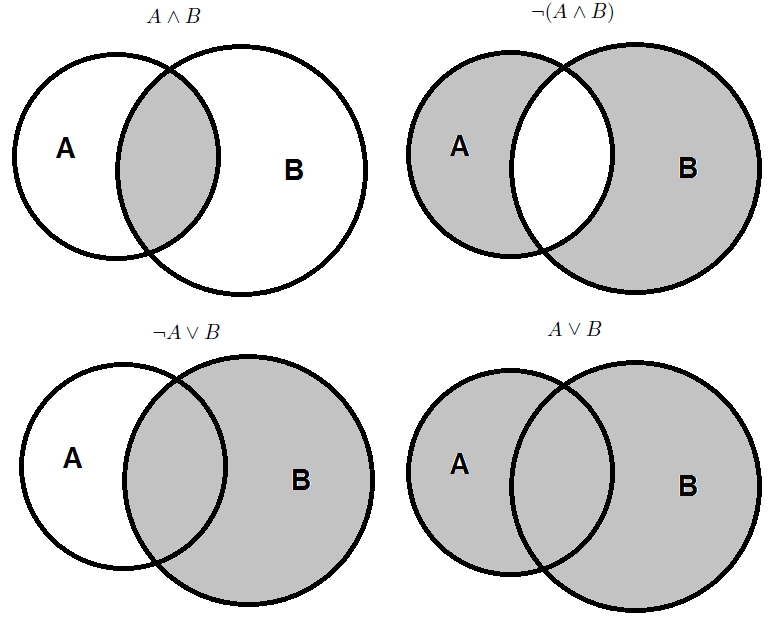
Графы
Радиус, диаметр и центры графа
Эксцентриситет вершины графа — расстояние до максимально удаленной от нее вершины. Радиус графа — минимальный эксцентриситет вершин, а диаметр графа — максимальный эксцентриситет вершин. Центр графа образуют вершины, у которых эксцентриситет равен радиусу. Центр графа может состоять из одной, нескольких или всех вершин графа [Кирсанов М. Н. Графы в Maple. Задачи, алгоритмы, программы. — М.: Издательство ФИЗМАТЛИТ, 2007. — 168 с.].
Задача. Дан граф с заданным весом ребер
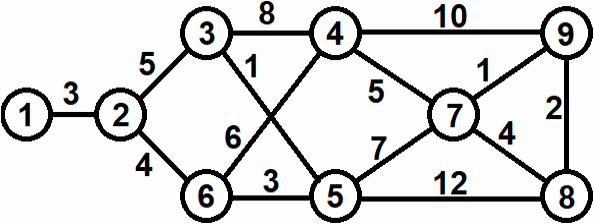 Найти
радиус, диаметр и центры графа.
Найти
радиус, диаметр и центры графа.
Решение
Заданы веса ребер, поэтому граф называется взвешенный. Программа на C++ в Visual Studio 2013:
#include "stdafx.h" // Visual Studio 2013
#include "algorithm" // для min, max в Visual Studio 2013
#include "iostream" // Visual Studio 2013
using namespace std;
int main(){
const int N = 9; // Количество вершин в графе
const int INF = 100000; // Число большее длины любого пути в графе
int i, j, k;
int d[9][9] = {
{ 0, 3, INF, INF, INF, INF, INF, INF, INF },
{ 3, 0, 5, INF, INF, 4, INF, INF, INF },
{ INF, 5, 0, 8, 1, INF, INF, INF, INF },
{ INF, INF, 8, 0, INF, 6, 5, INF, 10 },
{ INF, INF, 1, INF, 0, 3, 7, 12, INF },
{ INF, 4, INF, 6, 3, 0, INF, INF, INF },
{ INF, INF, INF, 5, 7, INF, 0, 4, 1 },
{ INF, INF, INF, INF, 12, INF, 4, 0, 2 },
{ INF, INF, INF, 10, INF, INF, 1, 2, 0 }
}; // Дистанции (вес) в графе
int e[N]; // Эксцентриситет вершин
int c[N]; // Центры графа
int rad = INF; // Радиус графа
int diam = 0; // Диаметр графа
// Алгоритм Флойда-Уоршелла
for (int k = 0; k<N; ++k)
for (int i = 0; i<N; ++i)
for (int j = 0; j<N; ++j)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
// Нахождение эксцентриситета
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
e[i] = max(e[i], d[i][j]);
}
}
// Нахождение диаметра и радиуса
for (int i = 0; i < N; i++) {
rad = min(rad, e[i]);
diam = max(diam, e[i]);
}
cout << "Diameter: " << diam << endl;
cout << "Radius: " << rad << endl;
// Центры графа
cout << "Centers: ";
for (int i = 0; i < N; i++) {
if (e[i] == rad) {
cout << i << "\t";
}
}
system("pause"); // Visual Studio 2013
return 0;
}
Остовные деревья
Остовное дерево неориентированного связного графа (spanning tree) G - его подграф, содержащий все вершины графа G и ребра графа G, не образующие циклы. Остов графа является деревом.
Задача. Построить все остовные деревья неориентированного графа из предыдущей задачи.
Решение
Алгоритм порождения всех каркасов неориентированного графа [Окулов С. М. Программирование в алгоритмах [Электронный ресурс] / С. М. Окулов.—5-е изд. (эл.).—М. : БИНОМ. Лаборатория знаний, 2014.—383 с.] реализован на C++ в Visual Studio 2013:
#include "stdafx.h"
#include "iostream"
using namespace std;
const bool Zero = 0; // Ноль
const int N = 9; // число узлов графа
bool A[N][N] =
{
{ 0, 1, Zero, Zero, Zero, Zero, Zero, Zero, Zero },
{ 1, 0, 1, Zero, Zero, 1, Zero, Zero, Zero },
{ Zero, 1, 0, 1, 1, Zero, Zero, Zero, Zero },
{ Zero, Zero, 1, 0, Zero, 1, 1, Zero, 1 },
{ Zero, Zero, 1, Zero, 0, 1, 1, 1, Zero },
{ Zero, 1, Zero, 1, 1, 0, Zero, Zero, Zero },
{ Zero, Zero, Zero, 1, 1, Zero, 0, 1, 1 },
{ Zero, Zero, Zero, Zero, 1, Zero, 1, 0, 1 },
{ Zero, Zero, Zero, 1, Zero, Zero, 1, 1, 0 }
}; // Матрица смежности
bool Nnew[N]; // признак, просмотрена вершина графа или нет
int Turn[N]; // очередь
int Tree[2][N]; // список ребер, образующих каркас
int Down; // нижний указатель
int Up; // верхний указатель
int numb; // число ребер в строящемся каркасе
int AllTrees; // Всего остовных деревьев
int i, k;
void Solve(int v, int q) // Номера вершин: v - из которой выходит ребро,
// q - начиная с которой следует искать очередное ребро каркаса
{
int j;
if (Down >= Up) return;
j = q;
while (j < N && numb<N - 1)
{
// Просмотр ребер, выходящих из вершины v
if (A[v][j] != 0 && !Nnew[j])
{
// Ребро включаем в каркас, так как вершина с номером j еще не в каркасе
Nnew[j] = true;
numb++;
Tree[0][numb] = v;
Tree[1][numb] = j;
Turn[Up] = j; Up++; // Включаем вершину j в очередь
Solve(v, j + 1); // Продолжаем построение каркаса
// Исключаем ребро из каркаса:
Up--; Nnew[j] = false; numb--;
}
j++;
}
if (numb == N - 1) // вывод каркаса
{
AllTrees = AllTrees + 1;
cout << "Tree N= " << AllTrees << endl;
for (i = 1; i <= numb; i++)
cout << Tree[0][i] + 1 << " " << Tree[1][i] + 1 << endl;
return;
}
/*Все ребра, выходящие из вершины с номером v, просмотрены.
Переходим к следующей вершине из очереди и так до тех пор,
пока не будет построен каркас.*/
if (j = N + 1)
{
Down++;
Solve(Turn[Down], 1);
Down--;
}
}
void main()
{
Nnew[0] = true;
Nnew[1] = false;
Turn[0] = 0; Down = 0; Up = 1; // в очередь первую вершину
numb = 0;
AllTrees = 0;
cout << "N*N: " << endl;
for (i = 0; i<N; i++)
{
for (k = 0; k<N; k++)
cout << " " << A[i][k]; // Матрица смежности графа
cout << endl;
}
Solve(Down, Up);
cout << "All trees: " << AllTrees << endl;
cout << "Press any key " << endl;
system("pause>>void");
}
Конец выполнения программы:
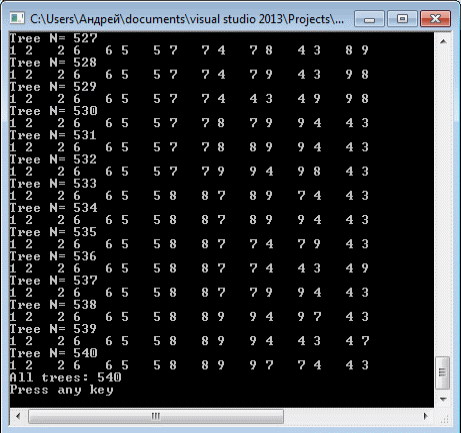
Остов минимального веса. Алгоритм Крускала
Остовом минимального веса является остов, содержащий ребра с минимальным весом.
Алгоритм Крускала используется для построения графа минимального веса. Для этого к пустому графу на множестве вершин заданного графа G присоединяются ребра, выбирая всякий раз ребра минимального веса, не образующие циклов с ранее присоединенными ребрами.
Элементы теории кодирования. Схема кодирования и декодирования
Исходное сообщение.
Кодирование сообщения кодом, контролирующим ошибки (d ≥ 3). Например, кодом Хэминга.
Передача по информационному каналу или хранение сообщения (могут появиться ошибки).
Оценка кодового слова и исправление ошибок при их наличии средствами контроля и исправления ошибок кода.
Декодирование сообщения.
Выходное сообщение = исходному сообщению.
Код Хэмминга
Пусть r – контрольные биты (разряды, символы, позиции), тогда
n = 2r – 1 – длина кодовых слов,
k = 2r – 1 – r = n – r – число информационных битов,
получаем (n, k) – код Хэмминга.
d – минимальное кодовое расстояние (число позиций, в которых отличаются любые два кодовых слова между собой), для кода Хэмминга d = 3.
(n, k) – код с минимальным кодовым расстянием d можно назвать (n, k, d) – кодом.
Примеры кодов Хэмминга:
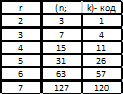
Граница Синглтона линейного кода
Граница Синглтона, названная в честь Сиглтона Р. К., устанавливает минимальное число контрольных символов в коде, контролирующем ошибки.
Код, содержащий алфавит из q элементов, называется q-ичным кодом. Если q = 2, то это двоичный код. Возможное число слов длиной n (мощность кода), составленных из q-ичного алфавита равно qn.
Пример двоичного кода, состоящего из 2 битов (разрядов, символов, позиций):
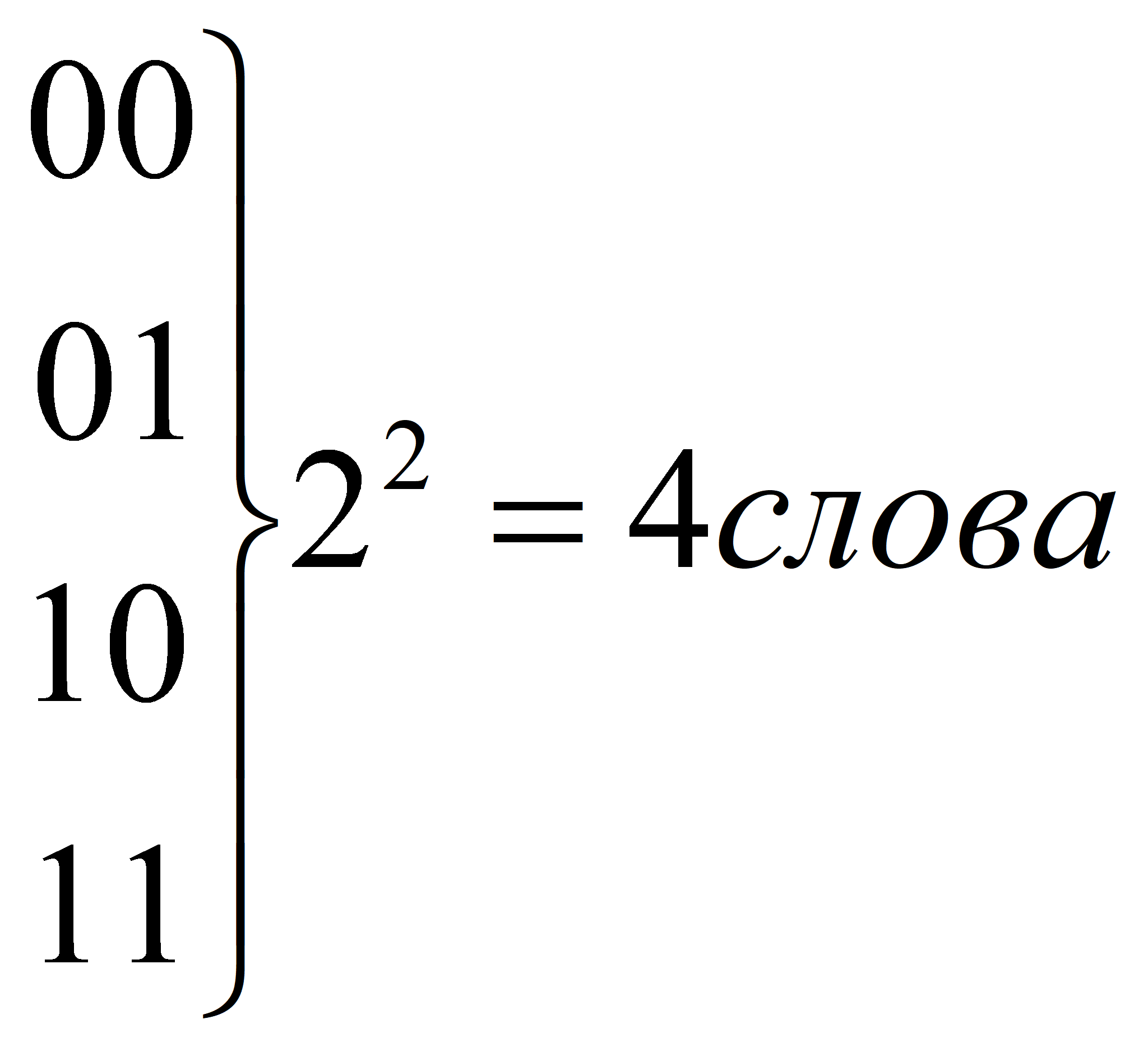
Если во всех словах кода убрать d – 1 символов, то оставщиеся n – (d - 1) символы представляют слова, отличающиеся как минимум в 1 позиции. Мощность (максимальное количество слов) такого кода qn – (d – 1).
Информационные символы в коде занимают k позиций. Возможное число слов (мощность) длиной k равна qk. Для линейных кодов граница Синглтона:
qk ≤ qn – (d – 1).
q > 1, следовательно
k ≤ n – (d – 1).
В неравенстве
n – k ≥ d – 1
n - k - это количество добавочных контрольных символов кода, контролирующего ошибки.
Список использованных источников с моими комментариями
Окулов С. М. Программирование в алгоритмах [Электронный ресурс] / С. М. Окулов.—5-е изд. (эл.).—М. : БИНОМ. Лаборатория знаний, 2014.—383 с.
Дискретная математика для школьников с алгоритмами на Паскале.
Калужнин Л.А. Что такое математическая логика? - М.: Наука, 1964. - 152 с.
Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. - М.: Вузовская книга, 2000. - 280 с.
Гиндикин С.Г. Алгебра логики в задачах. - М.: Наука, 1972. - 288 с.
Никольская И.Л. Математическая логика: Учебник. - М.: Высшая школа, 1981. - 127 с.
Зуев Ю.А. По океану дискретной математики: от перечислительной комбинаторики до современной криптографии. 2 тома. – М.: «Либроком», 2012.
Захарова Л.Е. Алгоритмы дискретной математики: Учебное пособие. – Моск. гос. ин-т электроники и математики. М., 2002, 120 с.
На Паскаль реализованы многие алгоритмы, графы. Имеется не большой список литературы, который полезно просмотреть.
Верещагин Н.К., Шень А. Лекции по математической логике и теория алгоритмов. Часть 1. Начала теории множеств. М.: МЦНМО, 1999. 128 с.
Хорошо представлена теория множеств, но некоторые значки не привычные.
Верещагин Н.К., Шень А. Лекции по математической логике и теория алгоритмов. Часть 3. Вычислимые функции. М.: МЦНМО, 1999. 176 с.
Графы
Кирсанов М. Н. Графы в Maple. Задачи, алгоритмы, программы. — М.: Издательство ФИЗМАТЛИТ, 2007. — 168 с.
Лаконично описана теория графов
Тюкарева М.Н. Метрические свойства графов. Дипломная работа. –Казань, 2014 - 32 с.
Подробно теория графов и алгоритмы определения радиуса, диаметра, центров графа
Альпин Ю.А., Ильин С.Н. Дискретная математика: графы и автоматы. Учебное пособие. — Казань: Казанский государственный университет им. В.И. Ульянова-Ленина, 2006. — 78 с
Лаконично!
Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978, - 432 с.
Сайт: super-code.ru
©